1.矩阵乘法
说白了就是
c[i][j] = a[i][k] * b[k][j]
2.矩阵快速幂
就是把快速幂中整数乘法换成了矩阵乘法
struct ma
{
int m[5][5];
}ans,base;
ma cal(ma a,ma b)
{
ma tmp;
for(int i = 1;i <= 2;i++)
{
for(int j = 1;j <= 2;j++)
{
tmp.m[i][j] = 0;
for(int k = 1;k <= 2;k++) tmp.m[i][j] += a.m[i][k] * b.m[k][j];
}
}
return tmp;
}//矩阵乘法
int qpow(int ci)
{
base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;
base.m[1][1] = 0;
ans.m[0][0] = ans.m[1][1] = 1;
ans.m[0][1] = ans.m[1][0] = 0;//初始化矩阵(因题而异)
while(ci)
{
if(ci & 1)
{
ans = cal(ans,base);
}
base = cal(base,base);
ci >>= 1;
}
return ans.m[0][1];
}//快速幂,把整数乘法换成矩阵乘法
或者在结构体中重载运算符
求\(Fibonacci\)数第\(n\)项
用矩阵运算
先写与斐波那契数递推式直接相关:
\[\begin{bmatrix}f_n \\\\ \end{bmatrix}=\begin{bmatrix}1&1\\&\end{bmatrix} \times \begin{bmatrix}f_{n-1}\\f_{n-2}\end{bmatrix}
\]
再补齐左边
\[\begin{bmatrix}f_n \\f_{n-1}\end{bmatrix}=\begin{bmatrix}1&1\\&\end{bmatrix} \times \begin{bmatrix}f_{n-1}\\f_{n-2}\end{bmatrix}
\]
补齐矩阵
\[\begin{bmatrix}f_n \\ f_{n-1}\end{bmatrix}=\begin{bmatrix}1&1\\1&0\end{bmatrix} \times \begin{bmatrix}f_{n-1}\\f_{n-2}\end{bmatrix}
\]
再递归下去:
\[\begin{aligned}\begin{bmatrix}f_n \\ f_{n-1}\end{bmatrix}&=\begin{bmatrix}1&1\\1&0\end{bmatrix} \times \begin{bmatrix}f_{n-1}\\f_{n-2}\end{bmatrix}
\\&= \begin{bmatrix}1&1\\1&0\end{bmatrix} \times \begin{bmatrix}1&1\\1&0\end{bmatrix} \times \begin{bmatrix}f_{n-2} \\ f_{n-3}\end{bmatrix}
\\&= \cdots
\\&= \begin{bmatrix}1&1\\1&0\end{bmatrix}^{n-1}\times \begin{bmatrix}f_{1} \\ f_{0}\end{bmatrix}\end{aligned}\]
前面部分使用矩阵快速幂解决
更多肥不拉几
前缀和\(S_n(s_n)\)
由\(s_n = s_{n-1}+f_n\)得
\[\begin{bmatrix}s_n \\\\\\\end{bmatrix}=\begin{bmatrix}1&1&\\\\&\end{bmatrix} \times \begin{bmatrix}s_{n-1}\\f_n\\\\\end{bmatrix}
\]
右边两者下标差\(1\),补矩阵
\[\begin{bmatrix}s_n \\f_{n+1}\\\\\end{bmatrix}=\begin{bmatrix}1&1&0\\0 & 1 & 1\\&\end{bmatrix} \times \begin{bmatrix}s_{n-1}\\f_n\\f_{n-1}\\\end{bmatrix}
\]
再按下标关系搞
\[\begin{bmatrix}s_n \\f_{n+1}\\f_n\end{bmatrix}=\begin{bmatrix}1&1&0\\0 & 1 & 1\\0&1&0\end{bmatrix} \times \begin{bmatrix}s_{n-1}\\f_n\\f_{n-1}\\\end{bmatrix}
\]
递归
\[\begin{bmatrix}s_n \\f_{n+1}\\f_n\end{bmatrix}=\begin{bmatrix}1&1&0\\0 & 1 & 1\\0&1&0\end{bmatrix}^{n-1} \times \begin{bmatrix}s_{1}\\f_2\\f_{1}\\\end{bmatrix}
\]
求\(T_n = \sum\limits_{i = 1}^n(if_i)\)
\[\begin{aligned}T_n &= f_1 + 2f_2 + 3f_3 + \cdots + nf_n\\&=nS_n - S_{n-1} - S_{n-2} - \cdots - S_1\\&=nS_n - \sum\limits_{i = 1}^{n-1}S_{i}\end{aligned}
\]
设\(P_n = \sum\limits_{i = 1}^{n-1}S_{i}\),则
\[T_n = n \times S_n - P_n
\]
用矩阵计算\(S_n,p_n\),然后求\(T_n\)
由\(P_n = P_{n - 1} + S_{n-1}\)
\[\begin{bmatrix}P_n \\\\\\\end{bmatrix}=\begin{bmatrix}1&1&&\\\\&\end{bmatrix} \times \begin{bmatrix}P_{n-1}\\S_{n-1}\\\\\end{bmatrix}
\]
由\(S_n = S_{n-1}+f_n,f_{n+1} = f_n + f_{n-1}\)补
\[\begin{bmatrix}P_n \\S_n\\f_{n+1}\\f_n\end{bmatrix}=\begin{bmatrix}1&1&0&0\\0&1&1&0\\0&0&1&1\\0&0&1&0\end{bmatrix} \times \begin{bmatrix}P_{n-1}\\S_{n-1}\\f_n\\f_{n-1}\end{bmatrix}
\]
递归
\[\begin{bmatrix}P_n \\S_n\\f_{n+1}\\f_n\end{bmatrix}=\begin{bmatrix}1&1&0&0\\0&1&1&0\\0&0&1&1\\0&0&1&0\end{bmatrix}^{n-1} \times \begin{bmatrix}P_{1}\\S_{1}\\f_2\\f_{1}\end{bmatrix}
\]
选拔队员
click
还以为是个组合,但是男女人数任意,所以不是
设\(dp(i,0/1)\)表示第\(i\)位坐的是男生(0)还是女生(1)
如果坐的是男生,那么前一位随便
\[dp(i,0) = dp(i - 1,1) + dp(i - 1,0)
\]
如果该位是女生,那么前一位必须是男生
\[dp(i,1) = dp(i - 1,0)
\]
\[\begin{aligned}
ans(i) &= dp(i,0) + dp(i,1) \\&= dp(i - 1,1) + dp(i - 1,0) + dp(i-1,0)\\&=ans(i - 1)+dp(i - 1,0)
\\&=ans(i - 1) + dp(i - 2,1)+dp(i-2,0)
\\&=ans(i-1) + ans(i-2)
\end{aligned}\]
wtf竟然是肥不拉几数列
初始化:\(dp(1,0) = dp(1,1) = 1\)
即\(ans(1) = 2\)
所以
\[ans(i) = f_{i+2}
\]
直接一个矩阵
3.经验之谈
对于\(f_n = af_{n-1}+bf_{n-2} + c\)
\[\begin{bmatrix}f_n\\f_{n-1}\\c\end{bmatrix}=\begin{bmatrix}a&b&1\\1&0&0\\0&0&1\end{bmatrix}\times \begin{bmatrix}f_{n-1}\\f_{n-2}\\c\end{bmatrix}
\]
对于\(f_n = c^n - f_{n-1}\)
\[\begin{bmatrix}f_n\\c^n\end{bmatrix}=\begin{bmatrix}-1&c\\0&c\end{bmatrix}\times \begin{bmatrix}f_{n-1}\\c^{n-1}\end{bmatrix}
\]
4.分块矩阵
\(A\)是一个矩阵
如果让\(\begin{bmatrix}S_k\\A^k\end{bmatrix}\)和\(\begin{bmatrix}S_{k-1}\\A^{k-1}\end{bmatrix}\)建立关系,则
\[\begin{bmatrix}S_k\\A^k\end{bmatrix}=\begin{bmatrix}1&A\\0&A\end{bmatrix}\times \begin{bmatrix}S_{k-1}\\A^{k-1}\end{bmatrix}
\]
5.与图论的炸裂结合
已知一个用邻接矩阵存的图,求从\(a\)点走到\(b\)点恰好经过\(k\)条边(允许重复走)的方案数
举个例子
\[\begin{aligned}
A=\begin{bmatrix}
0&1&1\\1&1&1\\1&0&0
\end{bmatrix}
\end{aligned}\]
1表示两点间有边相连,0表示没有
尝试将矩阵乘起来,并选取一个方格观察
\[A^2=a_{11}\times a_{11}+a_{12}\times a_{21}+a_{13}\times a_{31}
\]
这时再结合矩阵乘法的规则
\[a_{i,j} \times a_{j,k}
\]
就发现只有二者的值均为1时才会对答案有贡献,就相当于\(i,j\)和\(j,k\)间均有边
那么,\(A^2\)就相当于\(i->j->k\),走了两步
所以,走\(k\)步就是\(A^k\),答案就是\(A_{a,b}\)
6.更多逆天结合
P2886 [USACO07NOV] Cow Relays G
click
设\(dp(i,j)\)表示到\(i\)点经过\(j\)条边的方案数
\[dp(i,j) = \min\limits_{k = 1}^{n}(dp(k,j - 1)+w_{k,i})
\]
\[\text{如果k,i间有边,w就是边权,否则就是正无穷表示不联通}
\]
再想一想,结合上面矩阵的表示法,我们可以尝试用
\(w_{i,j}+w_{j,k}\)表示\(i\to j\to k\),那么每次矩阵运算就变成了
\[ans_{i,j} = \min(ans_{i,j},w_{i,j} + w_{j,k})
\]
\(Floyd\)友情客串但不是,这里只是单纯的矩阵乘法改版,\(Floyd\)数组里存的直接是最短路
接下来考虑这种形式能否使用快速幂加速
\(\min\)肯定无所谓
考虑到快速幂中有更新底数这一步,那么是否能更新\(w\)矩阵,废弃初始存的边来加速呢
意淫的讲,可以,更新\(w\)就相当于把原先的一条一条的边拼起来
专业的讲,矩阵满足结合律
\[\begin{aligned}
(AB)C &= \min\limits_{l = 1}^{c}(\min\limits_{k = 1}^{b}(A_{i,k}+B_{k,l})+C_{l,j})
\\&= \min\limits_{l = 1}^{c}\min\limits_{k = 1}^{b}(A_{i,k}+B_{k,l}+C_{l,j})
\\&= \min\limits_{k = 1}^{b}(A_{i,k}+\min\limits_{l = 1}^{c}(B_{k,l}+C_{l,j}))
\\&= A(BC)
\end{aligned}
\]
P4159 [SCOI2009] 迷路
click
与上面不同的是,要求变成了走过的边的边权和是\(T\),这样的话就不知道要走多少条边了
但可以转化
把边权都变成1就行了
怎么变呢?
Trick:拆点
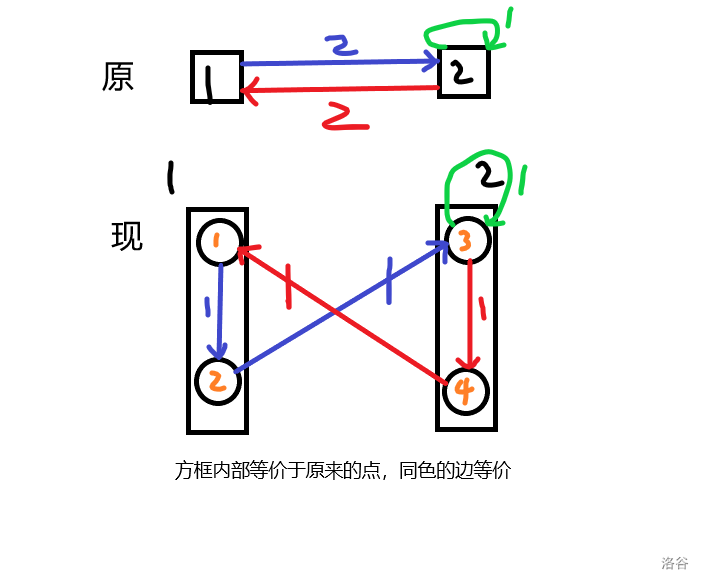
上面的矩阵是
\[A_0=\begin{bmatrix}0&2\\2&1\end{bmatrix}
\]
拆完的是
\[A=\begin{bmatrix}0&1&0&0\\0&0&1&0\\0&0&1&1\\1&0&0&0\end{bmatrix}
\]
平方一下
\[B=A^2=\begin{bmatrix}0&0&1&0\\0&0&1&1\\1&0&1&1\\0&1&0&0\end{bmatrix}
\]
假设\(T=2\),则\(ans=1\)
在下面的矩阵中,原来的\(1\to2\)变成\(2\to3\),而
\(B_{2,3} =1\),成立
这样可行,而且\(n \leqslant 10\),若一个点连的边的权是\(val\),那么这个点会被拆成\(val\)个,再结合读入方法,可知边权小于\(10\)。说明拆完点后的矩形大小在\(10^2\)左右,可以承受
更进一步的,我们把\(1\)分为两类:自连边(方框内)和已知边(跨方框)
int idx(int i,int j)
{
return (i - 1) * 10 + j;
}//把点(i,j)映射到100*100的矩阵(本题极限)里
void init()
{
for(int i = 1;i <= n;i++)
{
for(int j = 1;j < M;j++)//M:最大边权
A.m[idx(i,j)][idx(i,j + 1)] = 1;//自连边
for(int j = 1;j <= n;j++)
{
int x;
scanf("%1d",&x);
if(x) A.m[idx(i,x)][idx(j,1)] = 1;//本来就有的边
}
}
}
P3193 [HNOI2008] GT考试
click
\(dp+KMP+\text{矩阵}\)
设\(dp(i,j)\)表示\(X\)串配到了第\(i\)位,这\(i\)位匹配到了\(A\)串的第\(j\)位,就是这\(i\)位的\(X\)串的长为\(j\)的后缀和\(A\)串的长为\(j\)的前缀匹配
对于第\(i\)位新加的\(X_i\)
\[dp(i,j) = 0
\]
\[dp(i,j) = dp(i-1,j-1)
\]
但事实上不止也不完全一定是这两种情况,有可能新加的字符与前\(j-1\)个字符合在一起后无法匹配,有可能与前若干个字符合在一起后可以匹配
也就是说,可以从\([0,j-1]\)中所有长度转移
那么就要枚举第二维,此时也不一定非得加一个字符了
\[dp(i,j) = \sum\limits_{k = 0}^{j - 1}dp(i-1,k) \times w(k,j)
\]
\[\text{$w_{j,k}$表示长度由$k$扩展到$j$的方案数}
\]
事实上,我们知道了\(A\)串,那么\(w\)是能用kmp预处理出来的
看形式知矩阵乘法
为了确定矩阵,我们把\(dp\)方程改一下
\[dp(i,j) = \sum\limits_{k = 0}^{m - 1}dp(i-1,k) \times w(k,j)
\]
\(dp\)的矩阵大小就是\(n\times m\),\(w\)的大小就是\(m \times m\)
然后答案就是\(\sum\limits_{i = 0}^{m - 1}dp(n,i)\)
但\(N \leqslant 10^9\),开都开不出来
事实上,开\(m \times m\)就行了,\(n\)那部分相当于运算次数,用快速幂打成log就行了
就是\(w^n\)
答案\(ans=\sum\limits_{i = 0}^{m - 1}dp(0,i)\)
为什么是\(dp(0,i)?\)根据本质,dp数组就是\(w\)数组,所以就是\(0 \sim [0,m - 1]\)部分匹配方案数之和



 浙公网安备 33010602011771号
浙公网安备 33010602011771号