数论+组合
注：引理见后面第四部分
1.欧拉函数，欧拉筛及应用
1.欧拉筛：
for(int i = 2;i <= N;i++)
{
if(!vis[i]) pri[++cnt] = i;
for(int j = 1;i * pri[j] <= N;j++)
{
int u = i * pri[j];
vis[u] = 1;
if(i % pri[j] == 0) break;
}
}
2.欧拉函数：\(\varphi(n)\)
计算：\(\varphi(n) = n \times \prod _ {i = 1} ^ n (1 - \frac{1}{p_i})\)
用欧拉筛实现：
设 \(m = pri[j] \times i\)
1>若\(i \bmod pri[j] == 0\)
则
2>若\(i \bmod pri[j] != 0\),说明二者互质
则
2.定理
欧拉定理：
若\(\gcd(a,m) = 1\)
则
裴蜀定理
设\(a,b \in Z\)
则存在\(x,y\),使得
推广1：存在\(x,y\),使得
推广2：存在\(X_1 \cdots X_n\),使得
扩展欧几里得
对方程\(ax + by = \gcd(a,b)\)（设\(\gcd(a,b) = d\)）
可得到
而\(\gcd(a,b) = \gcd(b,a \% b)\)
则
又有\(a \% b = a - (int)a / b \times b\)
设\((int)a /b = k\)
则
整理得
则
这是相邻两组解的关系，那么这样推下去，则\(a\%b\)会变成\(0\)(求gcd时的终止条件)
则有
则存在特解
递归反推每一组解即可
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(b == 0)
{
x = 1;y = 0;
return a;
}
ll d;
d = exgcd(b,a % b,x,y);
ll t = x;
x = y;
y = t - a / b * y;
return d;
}
通解：
扩展欧拉定理
证明：
对于第一个式子，由欧拉定理
第二个式子用于\(b\)较小的时候
下证第三个式子
(分解质因数)
代入
\((\prod\limits_{i = 1}^{s}p_i^{r_i})^b \equiv (\prod\limits_{i = 1}^{s}p_i ^ {r_i})^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p\)
\(\prod\limits_{i = 1}^{s}(p_i^{r_i})^b \equiv \prod\limits_{i = 1}^{s}(p_i ^ {r_i})^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p\)
$\prod\limits_{i = 1}{s}p_ib \equiv \prod\limits_{i = 1}^{s}p_i ^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p $
即证明对
(在此之后，模数更换为\(m\)
即\(\forall 1 \leqslant i \leqslant s\)，\(p_i^b \equiv p_i ^{b \operatorname{mod} \varphi(m)+\varphi(m)} \pmod m\),并将\(p_i\)写成\(p\),\(p\)是质数)
如果\(\gcd(p,m) = 1\),则
如果不等于1，则\(m = k \times p(k \geqslant 2)\)
设\(m = s \times p^r,\gcd(s,p^r) = 1 = \gcd(s,p)\)
则
又有\(\varphi(m) = \varphi(p^r) \times \varphi(s)\)
那么\(p^{\varphi(m)} \equiv 1^{\varphi(p^r )}\equiv 1 \pmod s\)--------------①
又因为
并由①：\((p^{\varphi(m)})^{\lfloor \frac{b}{\varphi(m)} \rfloor} \equiv 1^{\lfloor \frac{b}{\varphi(m)} \rfloor} \equiv 1 \pmod s\)
故
(由引理)
则
\(p^{b+\varphi(m)}\equiv p^{b \operatorname{mod} \varphi(m)+ \varphi(m)}\pmod m\)（同乘\(p^{\varphi(m)-r}\)）
由①：
所以
证毕
\(Lucas\)定理
（\(p\)为素数）
证明：
首先：
其中\(0 < x < p,gcd(x,p) = 1\)
所以\(x\)的逆元存在
再由上
接下来
有\(x^m = x^{cp+d} = x^{cp} \times x^d\)
由\(\alpha,\beta\)式和系数相等：
\(C_{n}^{m} = C_{a}^{c} \times C_{b}^{d}\)
再结合\(n = ap + b,m = cp + d\)
\(C_{n}^{m} \equiv C_{n/ p}^{m / p} \times C_{n \%p}^{m\%p} \pmod p\)
中国剩余定理（CRT）
若
\(\forall1 \leqslant i < j \leqslant n,\gcd(m_i,m_j) = 1\)
那么
其中
\(M = \prod\limits_{i =1}^{n}m_i\)
\(c_i = \frac{M}{mi}\)
\(c_i^{-1}\)是\(c_i\)在模\(m_i\)意义下的逆元
证明：
首先：对\(x \equiv r_i \pmod {m_i}\),先不求余
再：
扩展中国剩余定理（exCRT）
若\(m_i\)不一定两两互质
最直观的：不求余中第一个注释处将不成立（\(\frac{M}{m_i} \% m_i != 0\)互质时必成立，但不互质时不一定），无法进行后续计算
EX:
对于
转化为
则
由裴蜀定理
\(\gcd(m_1,m_2) | (r_2 - r_1)\)时有解
特解与通解：（exgcd）
所以
那么
也就是说，两个方程可以合并成一个方程：
合并\(n - 1\)次即可
ExLucas(与Lucas无关)
求
其中\(p\)不一定是质数
设
那么只需求
再用\(CRT\)合并即可（得到的是和\(C_{n}^{m}\)同余的最小正整数）
考虑求
即
考虑到阶乘可能包含\(p\)因子，所以先除干净
即
其中\(x,y,z\)均为对应阶乘中含有的\(p\)因子数量
则再求
（分母那俩求逆元就行了）
考虑按是否是\(p\)的倍数划分阶乘
对于后面一坨，考虑到\(\operatorname{mod}\)有循环节，后面循环的部分可以直接“掏”掉若干次方的模数成为第一部分的循环节
比如：
其中后半部分循环节可以掏掉一个\(9\)变成第一部分
那么
前半部分是掏完模数的所有循环节，可以并成乘方，后半部分是剩的
所以
第一项要除掉，但第二项中可能还有\(p\)因子
所以定义
回到原式，即求
接下来求\(x,y,z\)
令\(g(n) = x\)（就是\(n\)的阶乘中有多少个\(p\)因子）
结合\(n!\)的展开式，可得
so~
合并即可
容斥原理
奇数个集合交集个数的系数为正，偶数个集合交集个数的系数为负
这实在没法证就那样不断修正后就这样了
3.乘法逆元
定义：若\(a \times x \equiv 1 \pmod b\),则\(x\)是\(a\)在模\(b\)意义下的乘法逆元，记为\(a^{-1}\)
使用：\((a/b) \% p = a \times b^{-1} \% p\)
| 方法 | 条件 | 时间复杂度 | 备注 |
|---|---|---|---|
| 费马小定理 | 模数为素数 | \(O(\log n)\) | |
| 欧拉定理 | \(\gcd(a,p) = 1\) | \(O(\sqrt{n})\) | |
| 扩展欧几里得 | \(\gcd(a,p) = 1\) | \(O(\log n)\) | 可以判断是否互质 |
| 线性递推 | 模数为素数 | \(O(n)\) |
exgcd:求\(ax+by=1\)中\(x\)的最小正整数解（如果有的话）
Fermat:可知\(a^{p - 1} \equiv 1 \pmod p\)
即\(a \times a^{p - 2}\%p \equiv 1 \pmod p\)
则\(a^{p - 2} \% p\)为逆元，快速幂求解
Euler:类似于Fermat,\(a^{\varphi(p)-1}\)为逆元
线性：对于质数\(p\),求\(1,2,\cdots,p - 1\)的逆元
设\(p = k \times i + r(1<i<p,r <i)\)
则\(k \times i + r \equiv 0 \pmod p\)
则
即\(inv[i] = - p / i \times inv[p \%i]\)
\(inv[1] = 1\)
保证非负：\(inv[i] = (p - p / i) \times inv[p \% i] \% p\)
4.结论/引理
任意互质的\(a,n\),满足\(a^x \equiv 1 \pmod n\)的最小x一定是\(\varphi(n)\)的约数
证明：若不是，则有
\(x \times k +r = \varphi(n)(r < x,k \in Z)\)
由已知：\(a^x \equiv a^{\varphi(n)} \equiv 1 \pmod n\)
则有\(a ^ {x \times k} \equiv 1^ k \equiv 1 \pmod n\)
进一步的：\(a^{x \times k + r} \equiv a ^ r \pmod n\) ------- a
又因为\(x\)已经最小，那么$a^r \(模\)n\(一定不为1（\)r < x$）
又由式子a可得：\(1\equiv a ^{\varphi(n)} \equiv a^r \pmod n\)
矛盾！
\(\gcd(a,b) = \gcd(a + k \times b,b)\)
证明：
设\(\gcd(a,b) = d\)
则\(a = p\times d,b = q \times d(gcd(p,q) = 1)\)
则
设\(m | p+k \times q,m|q\),则\(m | p\)
则\(\gcd(p+k \times q,q) = m = 1\)
则\(\gcd(a+k \times b,b) = d\)
若\(a \equiv b \pmod m\),则\(a \times k \equiv b \times k \pmod {m \times k}\)
证明：
\(a = s \times m + r\)
\(b = t \times m + r\)
\(a \times k - b \times k = (s - t)\times m \times k\)
则\(a \times k \equiv b \times k \pmod {m \times k}\)
组合
常见策略
-
特殊位置（元素）优先
-
相邻元素整体法（注意整体内部的排序与组合）
-
不相邻问题插空法
-
定序问题倍缩法（总数 / 定序部分的全排列数）
-
排列问题求幂法
-
环排问题线排策略
一般的，\(n\)个元素做圆形排列，排法为\((n - 1)!\)种
从\(n\)个不同元素中选择\(m\)个元素排列，排法为\(A_{n}^{m}/m\)种
-
多排问题直排策略
-
混合问题先选（\(C\)）后排（\(A\)）
-
平均分组问题除法策略
-
重排列（多部分定序）
-
隔板法：将\(n\)个物体分成\(m\)堆,每堆至少一个
等价为：在\(n - 1\)个间隔中插入\(m - 1\)个隔板（分成\(m\)部分）
允许堆空：\(C_{n + m - 1}^{m - 1}\)
错位排序
Catalan数
定义
应用：
(1).（典例/特征）从\((0,0)\)走到\((n,n)\),且路径不超过对角线的路径总数为\(H(n)\)
证明：
路径总数：\(C_{2n}^{n}\)（共\(2n\)步，其中\(n\)步向上/右）
对角线：\(y = x\)
非法路径超过对角线，说明与\(y = x + 1\)有交点
将该交点以后的路径关于\(y = x + 1\)对称，终点变为\((n + 1,n - 1)\)
也就是说，所有非法路径其实就是从\((0,0)\)到\((n + 1,n - 1)\)的所有路径
那么合法路径就是\(C_{2n}^{n} - C_{2n}^{n-1}\)
(2).\(n\)个元素进栈序列为\(1,2,\cdots,n\)，则出栈序列总数 = \(H(n)\)
将进栈抽象为走格子中向右走，出栈抽象为走格子中向上走，又因为一个元素进一次出一次，共\(2n\)次，那么就相当于：
从\((0,0)\)走到\((n,n)\)，任意时刻向上走的步数不能超过向右走的步数（出\(>\)入），也就是不超过对角线
显然的卡特兰数
(3).\(n\)对括号，能够匹配的序列总数
一共\(2n\)个符号，左括号\(n\)个，右括号\(n\)个，记答案为\(f(2n)\)（显然，括号里为字符数）
很显然，匹配的序列满足：任意一对括号中必有偶数个字符
我们选定一组括号作为分界，命名为括号\(W\)，左括号在第\(0\)位，那么右括号在
\(0 + 2 \times k\)（中间括号个数）$ + 1 = 2k + 1$处
每一个括号\(W\)的分布，对答案的贡献是
括号\(W\)内部的括号匹配排列数 \(\times\) 括号\(W\)外的括号匹配序列数
比如：括号\(W\)的位置为\(0,3\),那么内部有\(2\)个字符，外部有\(2n - 2 - 2 = 2n - 4\)个字符，那么贡献就是
那么
由于自变量是字符个数 \(= 2 \times\)括号个数\(n\)，实际上这个答案改成以个数为自变量就是
形式决定本质：鉴定答案为\(H(n)\)
类似的想法还有
\(n\)个节点的不同二叉树排列形式
非根结点总数\(n - 1\)，分成两部分（左右子树）排，无了，\(H(n)\)
一个凸多边形（顶点数为\(n\)）划分成三角形区域的方法数
先选定一个三角形把多边形分成两部分，该三角形占用3个顶点，那么左右的多边形节点总数为\(n +1\)个（三角形的一个顶点会被算两次）
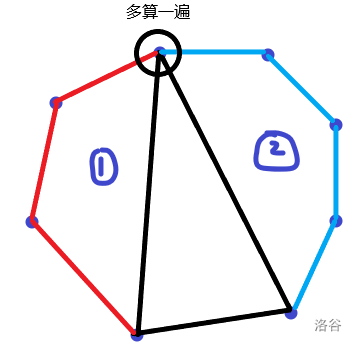
那么
总和为\(n - 1\)时答案为\(H(n)\)，那么此时答案就是\(H(n - 2)\)
总结：\(Catalan\)数的运用场景
-
任取一个集合作为选定集合\(K\)，能将全集\(U\)（所有元素，大小为\(n\)）分成两个子集\(S,T\)，且两子集的大小的和一定，设为\(sum\)(具体数值依题而定)
-
那么每一种分割情况对答案的贡献就是
-
对应答案就是\(H(n - (sum - (n - 1)))\)
-
注意：\(S,T\)中的元素必须全部等价（括号和括号等价之类，不会受到元素性质影响），否则贡献成为\(C_{sum}^{|S|} \times f(|S|) \times f(|T|)\)
典例：P2606 排列计数，由于排列受大小影响，所以前面的组合数无法消去
对应一下：
-
括号类型中，选定集合为一组（个）括号，剩余括号根据是否在选定括号内分成两个集合，并且由于每次的选定集合大小一定，所以这两个集合大小之和一定
-
二叉树的排列中，选定集合为根节点，剩余节点根据左右子树分为两个集合，且由于根节点只有一个，所以这两个集合大小之和一定
-
典例中的走格子也是，不计非法时的和为\(2n\)，但是有一半的路径会被砍掉，和变成\(n\),又因为\(|S|=|T|\)属于边界条件算一次，所以和变为\(n - 1\)
Prufur序列
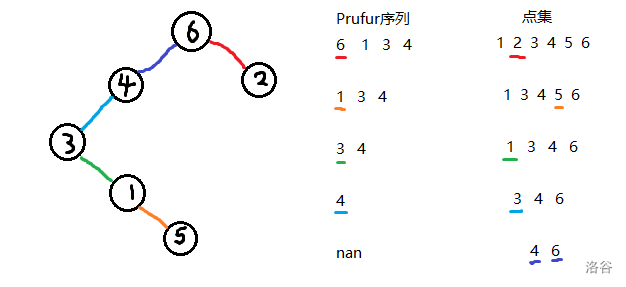
\(Prufur\)序列是用一个序列来表示无根树的东西，对于一颗\(n\)个节点的无根树，可以构造出唯一确定的长度为\(n - 2\)的\(Prufur\)序列
构造：
\(Tree -> Prufur\)
-
找到编号最小的叶子结点，将它的父节点计入序列
-
删去该叶子结点
-
重复上述过程直到剩下两个节点
如图
\(Prufur -> Tree\)
-
初始化一个点集为所有点
-
取出\(Prufur\)序列最前面的元素\(x\)
-
取出点集中不在\(Prufur\)序列中的最小编号\(y\)
-
连边，删去x,y
-
重复上述过程，在点集中最后剩下的两个点之中连一条边
如图
（还是以上图中的树为例）
性质：
-
一 一对应
-
度数为\(d_i\)的节点会在序列中出现\(d_{i - 1}\)次
其中，一一对应（双射）是非常有用的一条性质，这个性质可以让我们对数列（而不是树）进行排列组合以获得方案数而且不用担心重复（一个序列只对应一棵树，序列不同，树一定不同）
应用：
- 无向完全图的生成树数量：\(n^{n - 2}\)
很好理解：\(n - 2\)个空，每个空上可填\(1 \sim n\)
- 第\(i\)个节点的度数为\(d_i\) :
这就是一个重排列问题
如果有\(k\)个节点能进入序列，那么每个节点的出现次数一定是\(d_i - 1\)，由重排列得到\(\frac{A_{n - 2}^{n - 2}}{\prod\limits_{i = 1}^{k}A_{d_i - 1}^{d_i - 1}}\)
又因为\((1 - 1)! = 0\)所以叶子节点的度不影响结果，索性从\(1\)到\(n\)计算（也省去了求\(k\)的时间）
实际中，却总有一些逆天情况
- 若干节点的度数没有限制
设有\(m\)个节点没有度数限制，有\(k\)个节点有度数限制
设\(sum = n - 2 - \sum\limits_{i = 1}^{k}(d_i - 1)\)，表示剩下的节点还能出现几次
把未知度数的节点视为一个整体，运用重排列得到方案数：\(\frac{A_{n - 2}^{n - 2}}{\prod\limits_{i = 1}^{k}A_{d_i - 1}^{d_i - 1}\times sum!}\)
再考虑这个整体内部的方案数，由于无度数限制，直接随便排
BSGS
已知\(a,b,p,\gcd(a,p) = 1\)，求
的最小非负整数解
由扩展欧拉定理：\(a^x \equiv a^{x \operatorname{mod} \varphi(p)}\pmod p\)
因为\(\varphi(p) \leqslant p - 1 < p\)，所以\([0,p - 1]\)中一定有解
设\(x = im - j,m = \lceil \sqrt{p} \rceil,i \in [1,m],j \in [0,m - 1]\)
则
先枚举\(j\)，求出\(ba^j\)，用unordered_map存储\((ba^j,j)\)，如果关键字重复，用\(j\)大的替代旧的
再枚举\(i\),求出\((a^m)^i\)，如果表中有相同的结果，找到第一个（\(j\)最大）就结束，\(ans = im - j\)
斯特林数
第一类斯特林数： \(\begin{bmatrix}n\\m\end{bmatrix}\)
组合意义：让\(n\)个人坐\(m\)个圆桌（大小足够且不能有空桌）的方案数
递推：
解释：对于一个人，可以让他单独占一张桌子，也可以先让剩下\(n - 1\)个人坐\(m\)张桌子，然后把这个人插入这些人的左边，共\(n - 1\)种方案
第二类斯特林数：\(\begin{Bmatrix}n\\m\end{Bmatrix}\)
组合意义：将\(n\)个球放入\(m\)个盒子中（均相同而且要求非空）的方案数
与前者区别：圆桌即圆排列，但盒子内没有次序
递推：
解释： 对于一个小球，可以让他单独占一个盒子，或者其他小球先放，他随便放入一个盒子
