数论&组合例题思路

注：相关引理,方法证明见于数论+组合后面

1.构造一个只由8组成的数，使得它能被k整除并且长度最小

设答案长度为\(n\)

可得到

$ \frac{8 \times (10^n - 1)}{9} \equiv 0 \pmod k$

即

\[\begin{cases} 8 \times 10^n - 8 \equiv 0 \pmod k\\ 8 \times 10^n - 8 \equiv 0 \pmod 9 \end{cases} \]

\(8 \times 10^n \equiv 8 \pmod {9 \times k}\)

则 \(10^n \equiv 1 \pmod {\frac{9 \times k}{\gcd(8,k)}}\)

令 \(p = \frac{9 \times k}{\gcd(8,k)}\)

则当\(\gcd(10,p) = 1\)时，有

\(10^{\varphi(p)} \equiv 1 \pmod p\)

如果有解，则\(\gcd(10,p) = 1\),有答案为\(\varphi(p)\)，但不一定是最小

由引理：最小答案必是\(\varphi(n)\)的约数

所以\(\varphi(p)\)的约数\(r\)中最小的且满足

\(10^r \equiv 1 \pmod p\)

才是答案

2.\(ax \equiv 1 \pmod b\)的最小正整数解

转化：\(ax \equiv 1 \pmod b\) \(\to\) $ax = b(-y) + 1 $ \(\to\) \(ax + by = 1\)

由裴蜀定理：\(\gcd(a,b) = 1(\gcd(a,b) | 1)\) ------- 1

使用扩展欧几里得先求特解\((x_0,y_0)\)

由1式和通解形式可得通解

\(x = x_0 - b \times \frac{k}{\gcd(a,b)} \ (k \in Z)\)

找到合适的\(k\)即可得到最小正整数解

P1516 青蛙的约会

设跳了p次

由题:\(x + pm \equiv y + pn \pmod L\)

\((m - n)p\equiv y - x \pmod L\)

\((m - n)p = L(-k) + (y - x)\)

\((m - n)p + Lk = y - x\)

即看这个方程是否有解，若有，即求最小整数解

注意：\(m - n,y - x\)可能是负数

事实上，我们在解

\((m - n)p \equiv y - x\pmod L\)

由同乘性可以乘\(-1\)来变系数

a,b已知，求最小的k,使得\(yb \equiv k \pmod a\) 成立且\(y\)最小

\(k = \gcd(a,b)\)

求\(yb + xa = \gcd(a,b)\)的最小正整数解(\(y\))

P2421 荒岛野人

题意即为：求最小模数\(M\),使得对

$\forall 1 \leqslant i < j \leqslant n,c_i + p_i \times x \equiv c_j + p_j \times x \pmod M $

$(min(l_i,l_j)) < x $ 无解

$ x(p_i-p_j) \equiv c_j - c_i \pmod M$

\(x(p_i - p_j) + My = c_j - c_i\)

枚举\(M\)

记得给系数除\(\gcd\)

P2054 洗牌

先枚举：

1 2 3 4 5 6 7 8

5 1 6 2 7 3 8 4

7 5 3 1 8 6 4 2

8 7 6 5 4 3 2 1

4 8 3 7 2 6 1 5

2 4 6 8 1 3 5 7

2的坐标：\(2\to4\to8\to7\to5\to1\)

3的坐标：\(3\to6\to3\to6\to3\to6\)

\(\cdots\cdots\)

看到前面一部分是在\(\times 2\),但后面又变小。结合洗牌规则，\(\times 2\)应该仍存在，考虑取模

\(8 \times 2 = 16\)，\(16 \% 9 = 7\)

\(7 \times 2 = 14\)，\(14 \% 9 = 5\)

\(6 \times 2 = 12\)，\(12 \% 9 = 3\)

似乎得到：若起始坐标为\(x\),则终点为

\(x \times 2 ^ m \% (n + 1)\)(能过样例)

下证正确性

设目标数的坐标为\(x_0\)

我们以\(\frac{n}{2}\)为分界线，很明显，当一个数在分割线左边(\(x_0 \leqslant \frac{n}{2}\))时，洗完牌后他的位置将\(\times 2\)(分割线右边\(x_0\)个数在他前面，前面再有\(x_0 - 1\)个数，他自己就在\(2 \times x_0\)处)

接下来考虑在分割线右边的情况

设\(k=x_0 - \frac{n}{2}\)，则他前面(到分界线)有\(k - 1\)个数。

由规则可得到：下一次的位置会在\(2 \times k - 1\)(\(2 \times (k - 1) + 1\))

带入\(k\)的定义：\(2 \times k - 1 = 2 \times x_0 - n -1 = 2 \times x_0 - (n + 1)\)

可见：每洗一次牌，就相当于给原坐标乘以2再减去一个\(n + 1\).

由于每次减完后坐标一定在\(1-n\)之间，所以可以理解为取模

因此得到：\(x \times 2 ^ m \% (n + 1)\)

好的完成第一步(doge)

\(N \leqslant 10^{10}\),硬枚不行

那就求解：\(x \times 2 ^ m \equiv L \pmod {n + 1}\)

变形1：\(x \equiv L \times (2^m)^{-1}\pmod {n + 1}\)

变形2：\(x \times (2^m \% (n + 1)) \times L ^ {-1} \equiv 1 \pmod {n + 1}\)

这时发现：对于变形2：既不能保证\(n+1\)为质数，也不能保证\(\gcd(L,n+1) = 1\)，求逆元的方法均不能使用

而对于变形1，\(\gcd(2^m,n+1) = 1\)(\(n+1\)为奇数)

可以用扩欧或者欧拉定理

P2158 仪仗队

可以知道：长和宽的长度互质的矩形有一个顶点能被看到

那就不难了：求\(2\)到\(n - 1\)(\(n\)个人边长最大\(n - 1\))的欧拉函数并求和，再\(\times2\)（长宽可互换）

注意\(1\times1\)(\(4\)个人)中还能看见三个，要加上

P2303 Longge的问题

求\(\sum\limits_{i = 1}^{n} \gcd(i,n)\)

\(O(n) = 4,294,967,296\),暴力不可行 但能得分

若\(i\)与\(n\)互质，则\(\gcd(i,n) = 1\)

如果\(i\)是\(n\)的约数字，则\(\gcd(i,n) = i\)

设\(\gcd(i,n) = x\)的有\(k\)个

则

\[\begin{aligned} k &= \sum\limits_{i = 1}^{n}[\gcd(i,n) == x] \\&= \sum\limits_{i|x}[\gcd(\frac{i}{x},\frac{n}{x}) == 1] \end{aligned} \]

因为\(1 \leqslant i \leqslant n\),所以\(1 \leqslant \frac{i}{x} \leqslant \frac{n}{x}\)

令\(\frac{i}{x} = t\)

则\(k = \sum\limits_{t = 1}^{\frac{n}{x}}[\gcd(t,\frac{n}{x}) == 1] = \varphi(\frac{n}{x})\)

也就是说对于每个\(n\)的约数\(x\)，他对答案的贡献是
\(x \times k = x \times \varphi(\frac{n}{x})\)

则答案为：

\(\sum\limits_{x | n}x \times \varphi(\frac{n}{x})\)（对\(1\)也适用）

注意1：如果\(i\)是约数，那\(n/i\)也是。可以同时处理

注意2:如果遇到平方数，需要判断\(i != n / i\)后才能分别处理

P2155 沙拉公主的困惑

求\((\sum\limits_{i = 1}^{N!}[\gcd(i,M!) == 1] )\% R\)

设\(1 \leqslant p_1,p_2,\cdots p_n \leqslant M!\)是满足与\(M!\)互质的数(\(p_1 < p_2 < \cdots < p_n\))，那么个数为\(\varphi(M!)\)

由引理可知：\(\gcd(p_i,M!) = \gcd(p_i + l \times M!,M!)\)

也就是说，给每一个\(p_i\)加一个\(M!\),得到的\(\varphi(M!)\)个数依然与\(M!\)互质

则

\([1 ,M!]\)中有\(\varphi(M!)\)个数

\([1 + M! ,2 \times M!]\)中有\(\varphi(M!)\)个数

\([1 + 2 \times M! ,3 \times M!]\)中有\(\varphi(M!)\)个数

\(\cdots\)

\([1 + (r - 1)\times M!,r \times M!]\)中有\(\varphi(M!)\)个数

又\(r \times M! \leqslant N!\)

则\(r \leqslant \frac{N!}{M!}\)

即\(1 \leqslant r \leqslant \frac{N!}{M!},r \in Z\)

所以这样的区间一共\(\frac{N!}{M!}\)个

答案就是

\(\varphi(M!) \times \frac{N!}{M!}\)

接下来考虑\(\varphi(M!)\)的求法

尝试推广：阶乘的欧拉函数求法

用递推的方法，使用欧拉函数的积性函数性质

如果\(\gcd(M,(M - 1)!) = 1\),也就是说\(1-(M - 1)\)全都不是\(M\)的因数，那么\(M\)就是质数

\[\begin{aligned} \varphi(M!) &= \varphi((M - 1)!) \times \varphi(M) \\&= \varphi((M - 1)!) \times (M -1) \end{aligned} \]

否则，\(M\)就是合数，则\(M\)的最大质因子一定在\(1 - (M - 1)\)之间，也就是说\(M\)的所有质因子全部在\(1 - (M - 1)\)之间，那么

\[\begin{aligned} \varphi(M!) &= M! \times \prod\limits_{i = 1}^{k}(1 - \frac{1}{p_i}) \\&= M \times (M - 1)! \times \prod\limits_{i = 1}^{k}(1 - \frac{1}{p_i}) \\&= M \times \varphi((M - 1)!) \end{aligned} \]

但新的问题出现了:这样的递推是\(O(M)\)的。

\(O(TM)\)???（bushi）

啊看错了\(M \leqslant 10^7\)数组应该也许大概开的出来

直接预处理一遍后\(O(1)\)输出

\(O(M + T)\)

哦对了还有取模

首先看到求余后结果可能是0（先放到这里）

\(R\)是质数,则

\(\frac{\varphi(M!) \times N!}{M!} \% R = \varphi(M!) \times N!\times (M!)^{-1} \% R\)

\(OK\)再看怎么判断结果是\(0\)

如果\(N >= R\)，结果一定是0\(\cdots\cdots\cdots\)吗

这里又出现一个问题，回到式子

\(\varphi(M!) \times \frac{N!}{M!}\)

有这样的可能：\(N >= R\),但是\(\frac{N!}{M!}\)中\(N!\)的\(R\)因子全部被\(M!\)约掉了，即\(\frac{N!}{M!}\)可能并不是\(R\)的倍数

又引出一个问题：常用思路下会在分别预处理是直接取模，即对\(N!,M!\)分别取模，但是上面的可能直接否定了这一做法。

这说明了预处理的时候要避开\(\%R == 0\)的情形

那么，我们如果发现当前处理的数字是\(R\)的倍数，就直接把\(R\)全除完后再预处理（相当于把\(N!,M!\)中的\(R\)提前约掉）

那什么时候一定是0呢

那就是\(N!\)中的\(R\)的个数比\(M!\)中的多

也就是\(\lfloor \frac{N}{R}\rfloor > \lfloor \frac{M}{R} \rfloor\)

P4139上帝VS集合

略

组合

给定四个正整数 \(m\)、\(n\)、\(p\) 和 \(q\)（其中 \(p < m\) 且 \(q < n\)），在坐标系中有四个点$ A(0,0)\(、\)B(p,0)\(、\)C(m,q)$ 和 \(D(m,n)\) 的情况下，有多少对路径 \((f, g)\) 满足路径 $f $从点 \(A\) 出发到点 \(D\)，路径 \(g\) 从点 \(B\) 出发到点 \(C\)，且这两条路径不相交。

先画图

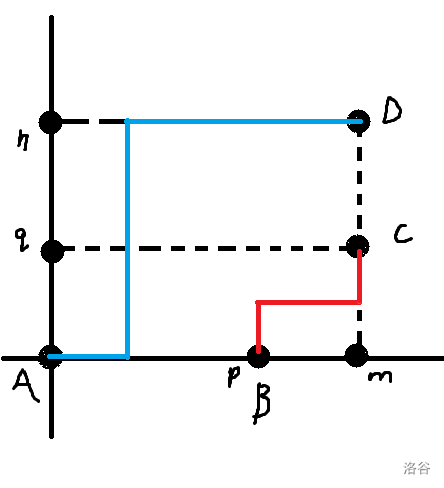
没有明显特征，看看非法路径

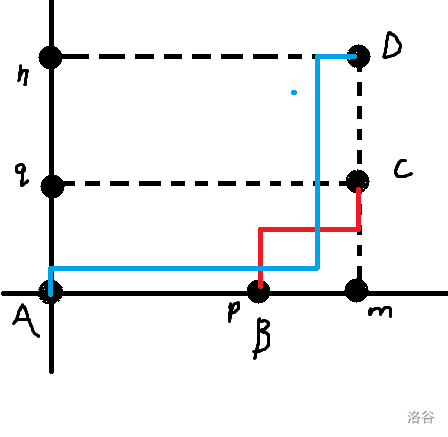
有交点\(\cdots\)，突然想起之前证明卡特兰数（详情见于数论+组合）中的非法路径

可以等效转化

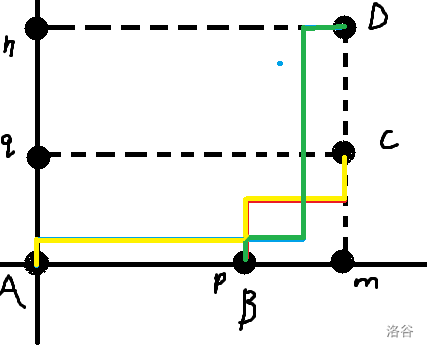
直接变成：从\(A\)到\(C\)，从\(B\)到\(D\)的路径组合数

那么直接整体\(-\)非法

\(ans = C_{m+n}^{n} \times C_{m - p + q}^{q} - C_{m+q}^{q} \times C_{m-p+n}^{n}\)

重点：等效替代法

P3223 排队

\(n\) 名男同学，\(m\)名女同学和两名老师排成一条直线，任意两名女同学不能相邻，两名老师也不能相邻，求排法。（注意：任意两个人都是不同的）

方法1：先插

男生无要求，排列\(A_{n}^{n}\)

把老师插入，方案\(A_{n+1}^{2}\)

插入女生，方案\(A_{n+3}^{m}\)

注意到这样的话老师之间必有男生，但也可以没有

将两个老师和一个女生打包，方案\(A_{2}^{2} \times C_{m}^{1}\)

再插入，方案\(n+1\)

插入剩下的\(m-1\)个女生：\(A_{n+2}^{m-1}\)

\(ans = A_{n}^{n} \times A_{n + 1}^{2} \times A_{n + 3}^{m} + 2m(n + 1)\times A_{n}^{n} \times A_{n+2}^{m-1}\)

方法2：先讨论

先排男生和老师

如果排完后老师挨在一起，方案数为\(A_{n+1}^{n+1} \times A_{2}^{2}\)

此时两个老师之间插入一个女生，方案\(2m\)

再将两个老师和插入的女生看作一个整体，方案\(A_{n+1}^{n+1}\)

再将剩的女生插进去，方案\(A_{n + 2}^{m - 1}\)

总数\(2mA_{n+1}^{n+1}\times A_{n+2}^{m-1}\)

如果老师不相邻，那么直接插

\((A_{n+2}^{n+2}-A_{n+1}^{n+1}A_{2}^{2})A_{n+3}^{m}\)

相加即可

平等的恨着每一道高精

[ABC156E] Roaming

有 \(n\) 不同个房间，每个房间有
\(1\) 个人。人可以在各个房间中移动（不能原地移动）。所有人一共移动了 $k $次，问最后各个房间人数排列有多少种情况。

手撕样例：

1 1 1

0 0 3

0 3 0

3 0 0

1 2 0

0 2 1

2 1 0

2 0 1

0 1 2

1 0 2

十种情况

显然，一次移动可以使一个仅一个人的屋子变成空屋，那么，最多产生几个空屋呢？

在上面的例子中，\(n > k\),所以最多产生\(k\)个空屋子，但如果\(n <= k\)，那么只能产生\(n - 1\)个空屋子（至少一个屋子有人）

对于有\(i\)个空屋子的情况，那么就有(\(n - i\))个屋子有人

把\(n\)个人放入（\(n - i\)）个屋子，每个屋子至少有一个人

选出空屋子后，有人的屋子同时也出来了，方案\(C_{n}^{i}\)

然后把\(n\)个人放入\(n - i\)个屋子里，隔板法，方案\(C_{n - 1}^{n - i - 1}\)

\(ans = \sum\limits_{i = 1}^{min(k,n - 1)}C_{n}^{i} \times C_{n - 1}^{n - i - 1}\)

求\(x\)的大于\(1\)的因子组成的满足任意前一项都能整除后一项的序列的最大长度，以及满足最大长度的序列的个数。

\(x = \prod\limits_{i = 1}^{k}p_i^{\alpha_i}\)

则

\(len_{max} = \sum\limits_{i = 1}^{k}\alpha_i = l\)(后面用)

(每次给前一项乘一个质因子就能得到下一项)

考虑计算个数

首先，选一个质因子作为第一项，方案数为\(k\),选完后对应的\(\alpha_i\)要减\(1\)

每次乘的时候从未用过的质因子中选

一个首项对应方案：\(\frac{A_{l - 1}^{l - 1}}{\prod\limits_{i = 1}^{k}A_{\alpha_i}^{\alpha_i}}\)（重排列）

将这\(k\)次方案的数量累加即可（由于修改的\(\alpha_i\)不一样，各方案之间结果可能不同，不能直接用乘法）

求在一个\(n\times n\)的国际象棋棋盘上放置\(k\)个车的方式数量，以确保它们之间不互相攻击

首先有解的前提：\(k <= n\)（一个占一整行）

先选出\(k\)行，方案\(C_{n}^{k}\)

再竖着看，初始有\(n\)个空列，每次在剩下的空列中选一个放棋子，选\(k\)次

方案\(C_{n}^{1} \times C_{n - 1}^{1} \times \cdots \times C_{n - (k - 1)}^{1} = \prod\limits_{i = 0}^{k - 1}C_{n - i}^{1}\)

相乘即可

P6191 [USACO09FEB] Bulls And Cows S

有\(n\)只牛，这些牛可以是公牛，也可以是母牛。牛们要站成一排，任意两只公牛之间至少要有\(k\)只母牛。
请计算一共有多少种排队的方法

首先，放一头公牛，则左右\(k\)个位置只能放母牛。

为了避免重复，我们默认第\(i+1\)头牛只能在第\(i\)头牛右边

这样，新放一个牛时只能从原来的位置\(-k\)中选（由于只在右边放，那么左边的\(k\)不考虑，所以只减一个\(k\)）

不放：\(1\)

放一个：\(C_{n}^{1}\)

放两个：\(C_{n - k}^{2}\)

\(\cdots\)

最多放：\(\lfloor\frac{n}{k + 1}\rfloor\)

\[ans = \sum\limits_{i = 0}^{\lfloor\frac{n}{k + 1}\rfloor}C_{n - k \times (i - 1)}^{i} \]

P3228 [HNOI2013] 数列

长度为\(k\)的序列，满足：最后一项不超过\(n\),每一项比前一项高出的值不超过\(m\),其中\(m(k - 1) < n\),求合法序列数

可以看到不确定因素非常多

索性抛开元素本身，直接考虑加法序列(日增长构成的序列)\(\{d_i\}\)

也就是差分数组（长度\(k - 1\)）

不考虑其他，有\(m^{k - 1}\)种加法序列

确定了加法序列，那么首项也会有一个范围

即\(1 \leqslant a_1 \leqslant n - \sum\limits_{i = 1}^{k - 1}d_i(d_i \in [1,m])\)

也就是说，一个加法序列对答案的贡献是\(n - \sum\limits_{i = 1}^{k - 1}d_i\)

接下来就是求这\(m^{k - 1}\)个贡献的和

首先提出来一个\(n \times m^{k - 1}\)，接下来看减掉了多少

对于\(d_1\)，\(d_1 = 1\)的情况是其他\(d_i\)把\(1\sim m\)取遍，为\(m^{k - 2}\)

\(d_1 \in [1,m]\)

则\(d_1\)的贡献为

$1 \times m^{k - 2} + 2 \times m ^{k - 2} + \cdots + m \times m ^{k - 2} $

即\(\frac{m(m + 1)}{2} \times m^{k - 2}\)

又一共\(k - 1\)个\(d\)

所以减掉的就是\((k - 1) \times \frac{m(m + 1)}{2} \times m^{k - 2}\)

\(ans = n \times m ^{k - 1} - (k - 1) \times \frac{m(m + 1)}{2} \times m^{k - 2}\)

P2606 [ZJOI2010] 排列计数

求\(1 \sim n\)的排列数\(\{p_i\}\)，满足

\[\forall i \in [2,n],p_i > p_{\lfloor i/2 \rfloor} \]

一眼二叉树结构，每个叶子比父亲要大（更专业的说法是堆）

设\(f[i]\)表示\(1 \sim i\)的方案数

树形结构是确定的，点的编号就那样，也必须那样（本人一开始没意识到这一点，乱分左右子树）

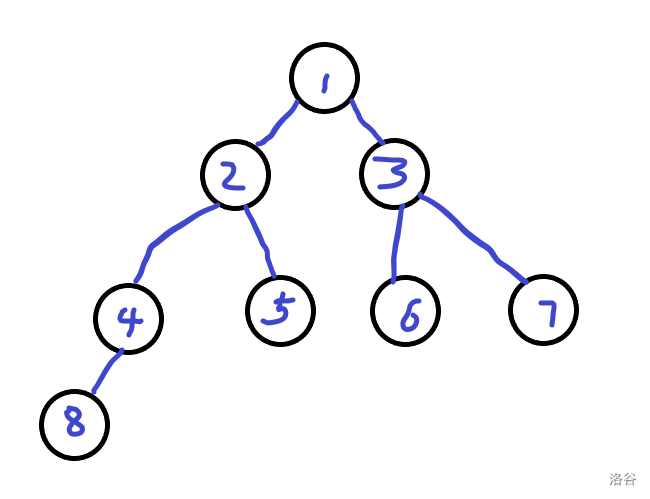
对于\(i\)个点

根节点是固定的（序列中最大值）

接下来就是分成左右子树来排

问题来了：如何得知对于\(i\)个节点，有多少在左子树，有多少在右子树？

对于标号为\(k\)的节点，它肯定在一个区间：\([2^p,2^{p+1}]\)

那就看看在中点左边还是在中点右边，就可以得知是在哪个子树

e.g:\(5 \in [2^2,2^3]\)

\(5 < (2^2+2^3) / 2 = 6\)，在左子树

\(1-i\)递推下来，设左子树大小为\(l\)，右子树大小为\(r\)，那么

\[f[i] = C_{i - 1}^{l} \times f[l] \times f[r] \]

一个有\(n\)个元素的集合有\(2^n\)个不同子集（包含空集），现在要在这\(2^n\)个集合中取出若干集合（至少一个），使得它们的交集的元素个数为\(k\)，求取法的方案数，答案模\(10^9 + 7\)

首先确定交集中的数，方案\(C_{n}^{k}\)

在含有选定的\(k\)个元素的情况下，把剩下的元素进行分配，方案\(2^{n - k}\)，也就是说含有选定的\(k\)个元素的子集数是\(2^{n - k}\)

在这些集合里选，很显然交集中一定有选定的\(k\)个元素，方案\(C_{n}^{k} \times (2^{2^{n - k}} - 1)\)（不能一个都不选）

但是更显然交集中可能还会有其他元素，所以这个答案范围过大，求的是交集至少为\(k\)
的方案数

设当前交集的元素个数是\(s\),则\(k \le s \le n\)

举个例子：当\(s = 2\)时，会把\(s = 3,s = 4,s = 5\)均算入答案

那么算了几次呢

比如说，对于\(s = 3\)的情况，假设数字为\(1,2,3\)，那么在\(s = 2\)中：

选定的数字是\(1,2\)时，会把\(1,2,3\)算入（因为至少两个，所以再配一个就成了\(s = 3\)的情况）

选定的数字是\(2,3\)时，会把\(1,2,3\)算入

选定的数字是\(1,3\)时，会把\(1,2,3\)算入

可以发现：对于\(s = 3\)，它在\(s = 2\)中被重复算了\(C_{3}^{2}\)次

也就是说，对于\(s = l\)的情况，它在至少为\(k\)的答案中被计算了\(C_{l}^{k}\)次

那么为了减去，就要给至少为\(3\)的答案乘一个\(C_{3}^{2}\)来匹配，符号为负

但又会影响\(s = 4 \cdots\)

容斥原理呗

\(s = 2\)中\(s = 4\)重复次数：\(C_{4}^{2}\)

\(s = 3\)中重复并算上乘的系数：\(C_{4}^{3} \times C_{3}^{2}\)

很显然\(s = 3\)的数大一些，则\(s = 4\)的符号为正（补足）

那系数呢

易知：\(C_{n}^{m} \times C_{m}^{k} = C_{n}^{k} \times C_{n - k}^{n - m}\)

代入化简：系数为\(C_{4}^{3} \times C_3^2 - C_{4}^{2} = C_{4}^{2}\)

类比可得\(s = 5\)系数为\(C_{5}^{2}\)，符号为负

从例子中可以得到答案：

对于至少为\(s\)次的答案，它的系数是\(C_{s}^{k}\)，符号为\((-1)^{s - k}\)

\[ans = \sum\limits_{i = k}^{n}(-1)^{i - k}C_i^k \times C_{n}^{i} \times (2^{2^{n - i}} - 1) \]

给定\(N\),\(L\)和\(R\)，统计长度在\(1 \sim N\)之间，元素大小都在 \(L\) 到 \(R\) 之间的单调不降序列的数量。输出答案对\(10^6+3\)取模的结果。

设长度为\(i\)时答案为\(f(i)\)

则

\[ans = \sum\limits_{i = 1}^{n}f(i) \]

（废话）

考虑求\(f(i)\)

可选的数字数\(s = R - L + 1\)

对于每一个可选的数，可以选择\(a_j\)个（\(a_j \geqslant 0\)）

那么

\[\sum\limits_{j = 1}^{s}a_j = i \]

对于每一种选法，总能排出唯一的序列，选法不同，序列不同，所以没有重复情况

经典隔板法:把\(i\)分成\(s\)堆，允许堆空

\[ans = \sum\limits_{i = 1}^{n} C_{i + s - 1}^{s - 1},s = R - L + 1 \]

由

\[C_{n}^{m} = C_{n - 1}^{m} + C_{n - 1}^{m - 1} \]

展开化简

\[\begin{aligned} ans &= \sum\limits_{i = 1}^{n} C_{i + s - 1}^{i} \\&= C_{s}^{1} + C_{s + 1}^{2} + \cdots + C_{s + n - 1}^{n} \\&= C_{s}^{0} + C_{s}^{1} + C_{s + 1}^{2} + \cdots + C_{s + n - 1}^{n} - C_{s}^{0} \\&= C_{s + 1}^{1} + C_{s + 1}^{2} + C_{s + 2}^{3} + \cdots + C_{s + n - 1}^{n} - 1 \\&= C_{s + 2}^{2} + \cdots + C_{s + n - 1}^{n} - 1 \\&= \cdots \\&= C_{s + n}^n - 1 \end{aligned} \]

P1450 [HAOI2008] 硬币购物

共有 \(4\) 种硬币。面值分别为 \(c_1,c_2,c_3,c_4\)。

某人去商店买东西，去了 \(n\) 次，对于每次购买，他带了 \(d_i\) 枚 \(i\) 种硬币，想购买 \(s\) 的价值的东西。请问每次有多少种付款方法。

这个肯定是要用背包哒

首先要学会背包求方案数

其实也没啥，定义\(dp[i][j]\)表示前\(i\)个物品装满容积为\(j\)的方案数

方程把求\(\max\)变成累加就行了

第一眼多重背包

然后我才不会说敲完后狂T但还有10分

说明要换背包

常见的有\(01\)背包求方案，完全背包求方案，\(01\)在此肯定不可取，难以扩展，考虑使用完全背包(无数量限制下的方案数)，然后剔掉非法方案数

非法方案可分为四大集合：第\(i\)种硬币超额使用

也就是减去这四个集合的并集

wc野生容斥

可得：并集大小 = 至少一种超额 \(-\) 至少两种超额（任意两个集合的交集） \(+\) 至少三种超额（任意三个集合的交集） \(-\) 至少四种超额（四个集合的交集）

全集：\(dp[s]\)（\(dp[i]\)表示价值恰好为\(i\)的方案数）

如果只有第\(i\)种硬币超额了，也就是说至少用了\(d_i + 1\)个硬币

那么在这种情况下的方案一定全部不合法，也就是一个\(s - c_i \times (d_i + 1)\)的背包所代表的方案全部不合法

即一种硬币超额的方案数为\(dp[s - c_i \times (d_i + 1)]\)

类似的可得两种硬币超额的方案是\(dp[i - c_i \times (d_i + 1) - c_j \times (d_j + 1)](i != j)\)，此时应当减去

三种的就是减去三个，四种的减去四个。

注意减的前提一定是够减（不够减说明该情况不存在）

算出来并集之后，再拿全集一减就行了

直接一个硬核枚举

		if(s >= c[0] * (d[0] + 1)) res += dp[s - c[0] * (d[0] + 1)];
		if(s >= c[1] * (d[1] + 1)) res += dp[s - c[1] * (d[1] + 1)];
		if(s >= c[2] * (d[2] + 1)) res += dp[s - c[2] * (d[2] + 1)];
		if(s >= c[3] * (d[3] + 1)) res += dp[s - c[3] * (d[3] + 1)];
		// 1个 
		if(s >= c[0] * (d[0] + 1) + c[1] * (d[1] + 1)) res -= dp[s - c[0] * (d[0] + 1) - c[1] * (d[1] + 1)];
		if(s >= c[0] * (d[0] + 1) + c[2] * (d[2] + 1)) res -= dp[s - c[0] * (d[0] + 1) - c[2] * (d[2] + 1)];
		if(s >= c[0] * (d[0] + 1) + c[3] * (d[3] + 1)) res -= dp[s - c[0] * (d[0] + 1) - c[3] * (d[3] + 1)];
		if(s >= c[1] * (d[1] + 1) + c[2] * (d[2] + 1)) res -= dp[s - c[1] * (d[1] + 1) - c[2] * (d[2] + 1)];
		if(s >= c[1] * (d[1] + 1) + c[3] * (d[3] + 1)) res -= dp[s - c[1] * (d[1] + 1) - c[3] * (d[3] + 1)];
		if(s >= c[2] * (d[2] + 1) + c[3] * (d[3] + 1)) res -= dp[s - c[2] * (d[2] + 1) - c[3] * (d[3] + 1)];
		//2个
		if(s >= c[0] * (d[0] + 1) + c[1] * (d[1] + 1) + c[2] * (d[2] + 1)) res += dp[s - c[0] * (d[0] + 1) - c[1] * (d[1] + 1) - c[2] * (d[2] + 1)];
		if(s >= c[0] * (d[0] + 1) + c[1] * (d[1] + 1) + c[3] * (d[3] + 1)) res += dp[s - c[0] * (d[0] + 1) - c[1] * (d[1] + 1) - c[3] * (d[3] + 1)];
		if(s >= c[0] * (d[0] + 1) + c[2] * (d[2] + 1) + c[3] * (d[3] + 1)) res += dp[s - c[0] * (d[0] + 1) - c[2] * (d[2] + 1) - c[3] * (d[3] + 1)];
		if(s >= c[1] * (d[1] + 1) + c[2] * (d[2] + 1) + c[3] * (d[3] + 1)) res += dp[s - c[1] * (d[1] + 1) - c[2] * (d[2] + 1) - c[3] * (d[3] + 1)];
		//3个 
		if(s >= c[0] * (d[0] + 1) + c[1] * (d[1] + 1) + c[2] * (d[2] + 1) + c[3] * (d[3] + 1)) res -= dp[s - c[0] * (d[0] + 1) - c[1] * (d[1] + 1) - c[2] * (d[2] + 1) - c[3] * (d[3] + 1)];
		//4个*/
		cout << dp[s] - res;//全 - 并

这里有一个小鸡俏 （就是让小鸡变美的方法）：用四个位来表示当前各集合是否参与交集，比如\(1101\)表示的是第一个，第二个和第三个集合的交集，范围即\(0001 \sim 1111(1 - 15 (1 << 4 - 1))\)

[ABC172E] NEQ

构造长为 \(N\) 的整数序列 \(A,B\) ，满足：

• \(1 \leq A_i,B_i \leq M\)
• \(\forall i\neq j\)，\(A_i\neq A_j,B_i\neq B_j\)
• \(\forall i\)，\(A_i\neq B_i\)

求合法构造方案数，对 \(10^9+7\) 取模。

第2个性质告诉我们序列中没有重复元素，则势必要选出\(M\)个数来造序列。不过\(A,B\)中所含的元素种类可能不尽相同

看到性质三，好像想到了些什么

不同，从排列时就保证该性质？

方法一： 错排

这个题中影响错排的重要因素就是\(A,B\)所含的元素种类

如果相同，无影响

考虑存在仅一个序列包含的元素时的情形

从错排的递推式下手

如果第\(n\)位的元素\(A\)中有，那么就是错排

\[D(n) = (n - 1) \times (D(n - 1) + D(n - 2)) \]

如果第\(n\)位的元素\(A\)中没有，则这个元素可以随意
“匹配”掉\(A\)中一位，只需对剩余的\(i - 1\)位错排

又因为\(B\)中备选的\(A\)中没有的元素一共\(M - N\)个，所以

\[D(n) = (M - N) \times D(n - 1) \]

二者合并后得到递推式

或者，总数 - 非法？

方法二：容斥

对于\(A\)的一个排列，对应的\(B\)共有\(A_{M}^{N}\)种排列（包含非法）

将非法情况分为：有\(i\)位相等，\(i \in [1,N]\)

如果有\(i\)位相等，先选出这\(i\)位来，那么剩下的\(n - i\)位由\(m - i\)个元素的排列补上，方案\(C_{N}^{i} \times A_{M - i}^{N - i}\)

由容斥：

非法总数 = \(\sum\limits_{i = 1}^{N}(-1)^{i - 1}C_{N}^{i} \times A_{M - i}^{N - i}\)

也就是说对于\(A\)的一种排列，合法数为\(A_{M}^{N} - \sum\limits_{i = 1}^{N}(-1)^{i - 1}C_{N}^{i} \times A_{M - i}^{N - i}\)

\(A\)又一共有\(A_{M}^{N}\)种排列，二者相乘即可

P2467 地精部落

求长度为\(n\)，\(h_i \in [1,n], \forall i \ne j,h_i \ne h_j\)的波动序列数（一个数不是山峰（比两边都大）就是山谷（比两边都小））

先康康波动序列的性质

• 交换不相邻的\(i,i + 1\)，会生成一个新的波动序列
• 若\(\{h_i\}\)是波动序列，则\(\{n - h_i\}\)也是一个波动序列

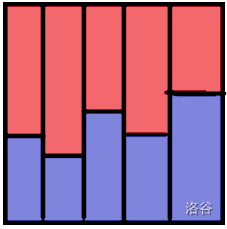
• 波动序列有对称性

首先数列有两大类：第一个是峰/谷

如果第一个是山峰，由性质2，倒一下就成第一项为山谷的情况了，所以不妨只考虑一种 ----- ①

设\(dp_{i,j}\)表示长度为\(i\)，第一项为\(j\)
，且第一项是山峰的序列总数

此时子情况就是第二项为山谷，第三项为山峰

再拿性质二倒一下，就变成了第二项为山峰，第三项为山谷的情况，符合\(dp\)状态，而且方案数不变

有两种方法让\(j\)成为山峰：

• 使用翻转，翻转完后\(j\)后面的山谷是\(j - 1\)，那么说明翻转前这里是山峰，高度\(i - (j - 1)\)，而且是后\(i - 1\)项的第一项

\[dp[i][j] += dp[i - 1][i - (j - 1)] \]

• 交换得来，将\(j\)与第一项交换，此时序列长度已经是\(i\)，根据交换条件，可知交换的是\(j - 1\)

\[dp[i][j] += dp[i][j - 1] \]

由①，最后答案要 \(\times 2\)

\[ans = 2 \times \sum\limits_{i = 1}^{n}dp[n][i] \% p \]

法二：组合

这样做会有一个难点：如何保证组合选取的时候不会出现重复元素？

有一件事是明确的：最大的数一定是山峰，记为\(h_{max}\)，所在处记为\(j\)

如果\(h_{max}\)在偶数位上，那么奇数位就是山谷，

此时我们将\(dp_{i,0/1}\)定义为：长度为\(i\)，开头为山峰/谷的方案数

那么：最大数前面数列的开头一定是山谷（\(1\)是奇数），后面数列的开头一定是山谷

又因为波动数列只与数的相对大小有关，所以不管选出来啥数字都可以排出来，而且有最大值做分割，因此左右互不影响，所以先给左边选数，选完后再论方案，是乘法原理

则

\[dp[i][0] += dp[j - 1][0] \times dp[i - (j + 1) + 1][0] \times C_{i - 1}^{j - 1} \]

（\(j \in [1,i],j = 2n,n \in N^+\)）

类似的可得奇数：

\[dp[i][1] += dp[j - 1][1] \times dp[i - (j + 1) + 1][0] \times C_{i - 1}^{j - 1} \]

（\(j \in [1,i],j = 2n + 1,n \in N^+\)）

最后

\[ans = dp[n][0] + dp[n][1] \]

P3330 [ZJOI2011] 看电影

蓝结论，黑高精

有\(K\)个座位，现执行以下步骤：

• 从\([1,K]\)中等概率选取一个数\(L\)

• 若\(L\)是空位，则坐下，否则\(L\) 加一，再判断是不是空位，以此重复

• 若第二步没找到空位，站着

共\(N\)人，求全班都有座位的概率

分母简单，\(k^n\)

考虑分子

由于标号存在诸多不确定性，我们换个入手点：椅子的状态

如果合法，那么要么坐满，要么有空座位

对于坐满的情况，我们补一个空座位，合并情况

为了统一，给本来就有空座位的情况也加一个空座位

也就是说，现在一共\(k + 1\)个座位，空座位有\(k + 1 - n\)个

由于此时考虑的都是合法情况，所以要找到构造方法使得在此方法下怎么选都是合法的

神之一笔就来了：连成环

不过很显然，这样会算进去一些非法方案，所以肯定要加以限制

由于现在是\(k + 1\)把椅子，有一把椅子是原本不存在的，那么很显然，这把椅子上只要不坐人，就是合法方案。

也就是说：一个\(k + 1\)的圆，其中一个座位不坐人的方法数

如果不考虑不能坐人的情况，方案\((k + 1)^{n}\)（反正都成环了，无论怎么选总能找到空位）

接下来砍掉重复的

这个环有\(k + 1\)个断点，可以形成\(k + 1\)个序列，那么也就是说每\(k + 1\)种选法只能形成一个环，所以方案数应为\(\frac{(k + 1)^n}{k + 1} = (k + 1)^{n - 1}\)

再考虑椅子不坐人的情况

从空椅子里抽一把不就好了

\[ans = \frac{(k + 1)^{n - 1} \times (k + 1 - n)}{k^n} \]

P2480 [SDOI2010] 古代猪文

求

\[g^{\sum\limits_{d | n}C_{n}^{d}} \operatorname{mod} 999911659 \]

\(g\)的系数太大了，肯定要取模

使用欧拉定理：

若\(gcd(g,999911659) = 1\)

则

\[g^{\sum\limits_{d | n}C_{n}^{d}} \equiv g ^{\sum\limits_{d | n}C_{n}^{d} \operatorname{mod} \varphi(999911659)} \pmod {999911659} \]

发现\(999911659\)是质数，所以\(\varphi(999911659) = 99991658\)

接下来交给\(exLucas\)

再快速幂一下就OK了

然而会T

发现\(999911658\)是四个质数的乘积，因此可以直接对这四个质数上普通\(Lucas\)再拿\(CRT\)合并

就好了

P2532 [AHOI2012] 树屋阶梯

用\(N\)个钢材搭建高度为\(N\)的阶梯，求方案数

考虑卡特兰数，那么就要和数论+组合中总结的\(Catalan\)的应用场景来对照

• 选出分割全集的集合，并且分成的两个子集大小和一定

考虑用一个钢材分成上下两部分

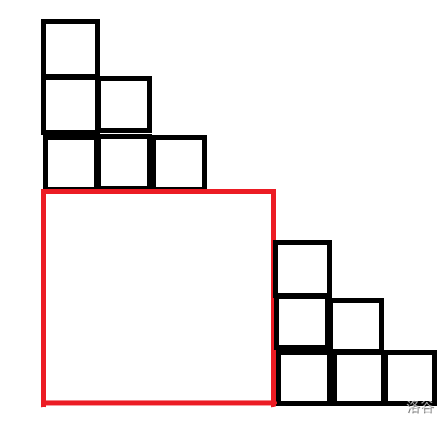
上面阶梯的级数是\(x\)，下面的级数是\(y\)，则\(x + y = N - 1\)，共用了\(N - 1\)个钢材（上面用\(x\)个，下面用\(y\)个），符合条件

而且分成的两部分是等价的

那么答案就是\(H(N - ((N - 1) - (N - 1))) = H(N)\)

上高精就行了

P3306 [SDOI2013] 随机数生成器

已知\(p,a,b,X_1,t\)

求使得

\[X_i =(a^{i - 1}X_1 + b\sum\limits_{j=0}^{i - 2}a^j) \equiv t \pmod p(i \geqslant 2) \]

成立的最小\(i\)（可以是\(1\)，即\(X_1 \equiv t \pmod p\)）

化简

\[\begin{aligned} X_i &= a^{i - 1}X_1 + b \times \frac{a^{i - 1 } - 1}{a - 1} \\&= a^{i - 1}X^1 + \frac{ba^{i - 1}}{a - 1} - \frac{b}{a - 1} \\&= a^{i - 1}(X_1 + \frac{b}{a - 1}) - \frac{b}{a - 1} \end{aligned} \]

所以

\[a^{i - 1}(X_1 + \frac{b}{a - 1}) - \frac{b}{a - 1} \equiv t \pmod p \]

\[a^{i - 1}(X_1 + \frac{b}{a - 1}) \equiv t + \frac{b}{a - 1} \pmod p \]

\[a^{i - 1}(X_1 + \frac{b}{a - 1}) \times (X_1 + \frac{b}{a - 1})^{-1} \equiv (t + \frac{b}{a - 1}) \times (X_1 + \frac{b}{a - 1})^{-1} \pmod p \]

\[a^{i - 1} \equiv (t + \frac{b}{a - 1}) \times (X_1 + \frac{b}{a - 1})^{-1} \pmod p \]

其中\(\frac{b}{a - 1} = b \times (a- 1) ^ {-1}\)，上述的\(-1\)次方均指逆元

上\(BSGS\)就行了

然后特判

• \(a = 0\)：\(X_i = b\)，判断\(b\)是否等于\(t\)

• \(a = 1\)：\(X_i = X_1 + b(i - 1)\)

\[i - 1 \equiv (t - X_1) \times b^{-1} \pmod p \]

• \(X_1 == t\)：\(ans = 1\)

[HNOI2009] 有趣的数列

求一个长度为 \(2n\) 的数列，满足：

• 它是从 \(1 \sim 2n\) 共 \(2n\) 个整数的一个排列 \(\{a_n\}_{n=1}^{2n}\)

• 所有的奇数项满足 \(a_1<a_3< \dots < a_{2n-1}\)，所有的偶数项满足 \(a_2<a_4< \dots <a_{2n}\)；

• 任意相邻的两项 \(a_{2i-1}\) 与 \(a_{2i}\) 满足：\(a_{2i-1}<a_{2i}\)。

答案对 \(p\) 取模。

（\(update:2024/1/12/22:32\)破\(1000\)行祭）

看样例知\(Catalan\)

证明：将这\(2n\)个数按性质三分成\(n\)组

设\(H(n)\)表示\(1\sim 2n\)的方案数

对照情景

• 选定分割集合：一组数，两边一共剩了\(n - 1\)组，和一定，数量上符合要求

接下来考虑等价性

设选的是第\(k\)组，那么前面\(k - 1\)组的方案应该是完全等价于\(H(k - 1)\)

即使有大的数跑进前面，小的数被挤到后面也不影响，因为相对关系没有改变，后面更大的数在\(1 \sim2(k - 1)\)中（前面）还是大数，小的数字在后面\(2k + 1 \sim 2n\)中还是小数

再结合两边集合的大小和事\(n - 1\)，所以

\[ans = H(n) \]

第二种理解方法：

结合性质可以得知：一个偶数位上的数字一定比他前面所有的数都大（比前面所有偶数大，比前一个奇数大，前一个奇数大于前面所有奇数）

我们现在把\(1 - 2n\)依次放到奇数或偶数位上，为了维护递增，显然每次都靠最左边放

那么，\(2i\)处只能放\(\geqslant2i\)的数

也就是说，前面\(1 - (2i-1)\)位已经放置完毕（这样才能轮到\(2i\)），而\(2i-1\)是奇数，所以奇数位比偶数位多

再算上第\(2i\)个，就变成了：

任意一次放置，都满足在偶数位上的数的数量小于等于在奇数位上的数的数量

拿进出栈一类比：偶数位代表出栈，奇数位代表进栈，发现

\[ans = H(n) \]

没说\(p\)是质数，上\(\text{exLucas}\)

然后你高高兴兴的发现exLucas被卡T了

真TMD是废物一个又容易T又不好写

狗都不写

那就换个方法：\(\frac{1}{n + 1}C_{2n}^{n}\)

这个一开始没有考虑是因为不能保证\(n + 1\)有逆元

那就约分上快速幂

拆开：

\[H(n) = \frac{\prod\limits_{i = n + 2}^{2n}i}{\prod\limits_{i = 1}^{n}i} \]

用欧拉筛预处理出\(1 - 2n\)内所有质数，把合数都劈成质数（可用倒序循环），统计下面各个质数有多少，再看上面的有多少，对应的质数个数一减就行了

P1463 [POI2001] [HAOI2007] 反素数

正整数 \(x\)约数的个数记作 \(g(x)\)。

如果某个正整数 \(x\) 满足：\(\forall 0 \lt i \lt x\)，都有 \(g(x) \gt g(i)\)，则称 \(x\) 为反质数。现试求不超过 \(N\) 的最大的反质数

这个题提到了一个有意思的东西：反质数

设\(n = \prod\limits_{i = 1}^{k}p_i^{c_i}\)是一个反质数，那么\(n\)一定满足：

• \(p_i\)是从\(2\)开始的连续的质数

• \(c_i\)单调不增

对于第一个，换成不连续的质数得到\(n'\)，在不改变次数的同时，很显然\(n' > n\)，但是\(g(n) = g(n')\)，这不符合反质数的定义

对于第二个，如果出现\(i < j,c_i < c_j\)，将\(p_i^{c_i}p_j^{c_j}\)换成\(p_i^{c_j}p_j^{c_i}\)得到\(n''\)，显然\(n'' > n\)（作比即可得），同样不符合定义

依靠这些性质，我们可以采用搜索的方法来“枚举”质数的次数，进而得到符合条件的数

给定一个正整数\(N\) ,它可以表示为 \(N = p^2q\)（\(p\)和 \(q\)是两个不同的质数且唯一）。找出\(p\)和\(q\)。

不想找

随表挑一个硬枚得50（枚\(q\)）

从小质数的开始枚分解质因数硬搞可过

求\(\frac{1}{x} + \frac{1}{y} = \frac{1}{n!}\)的正整数解\((x,y)\)的个数模\(10^9 + 7\)的结果

\[\frac{1}{y} = \frac{1}{n!} - \frac{1}{x} = \frac{x-n!}{xn!} \]

\[y = \frac{x-n!}{xn!} \]

\[y = \frac{1 - \frac{n!}{x}}{n!} \]

\(To\) \(Be\) \(Continued \cdots\)

(持续连载还不赶快点赞关注收藏）