dp的优化（单队，斜率）

1.单调队列优化\(dp\)

维护最小值：\(x \leqslant q.tail()\)

维护最大值：\(x \geqslant q.tail()\)

其实原理不难，当\(dp\)的转移源头是一个区间时，往往使用单调队列来维护区间最值（一般队列里装下标以方便维护区间大小，但也只是一般情况），节省了处理区间的时间（甚至噶掉一维），重点是对区间的处理方式和细节，以及处理什么区间都因题而异，因此直接结合相关情景来进行学习

P2564 [SCOI2009] 生日礼物（例题）

（正片开始）在某两个城市之间有 $ n $座烽火台，每个烽火台都有一个代价。要求连续 $ m $个烽火台中至少要有一个发出信号。求总共最少的代价

设\(dp[i]\)表示\(1 \sim i\)中选了\(i\)的方案

那么为了合法，只能从\([i - m ,i - 1]\)中转移

用单调队列优化，最简单的一类

和 P1725 琪露诺 很像

类似的还有最大子序和，就是拿前缀和搞（记得提前往队列里塞一个\(0\)）

P2627 [USACO11OPEN] Mowing the Lawn G

FJ有\(N\)只排成一排的奶牛，奶牛\(i\)的效率为\(E_i\)

计算没有连续的超过\(K\)只奶牛时可以得到的最大效率。

我们可以考虑从反面下手，找出不选的奶牛，将原来的序列分割成若干长度\(\leqslant k\)的区间

因此定义\(dp[i][1/0]\)表示选/不选第\(i\)头奶牛时的最大效率

如果不选，那么继承前一位的方案

\[dp[i][0] = \max(dp[i - 1][0],dp[i - 1][1]) \]

如果选了，那么在\([i - k,i]\)中必须有一个不选

\[dp[i][1] = \max(dp[j][0] + \sum\limits_{k = j + 1}^{i}E_k),j \in[i - k,i - 1] \]

拿前缀和优化：

\[dp[i][1] = \max(dp[j][0] +sum[i] - sum[j]) \]

对于枚举的\(j\)，\(sum[i]\)是固定的，那么把他弄出去

\[dp[i][1] = \max(dp[j][0] - sum[j]) + sum[i] \]

用单调队列维护\(dp[j][0] - sum[j]\)即可

单调队列优化多重背包

一个初学背包时的禁忌领域

先摆出多重背包的基本递推式

\[dp[n] = \max(dp[n],dp[n - k \times v] + k \times w),k \in[1,s],k \times v\leqslant n \]

发现每次都是多减去一个\(v\)，因此设\(n = pv + q\),那么

\[dp[n] = \max(dp[n],dp[i \times v + q]),i \in [0,\min(s,p)] \]

也就是说,\(dp[pv + q]\)只会从\(dp[i \times v + q]\)转移而来

后面的部分可以考虑使用单调队列，但别着急，还有\(w\)呢，对于不同的\(i\)，\(w\)的系数也不一样

举个例子：

\[dp[3v + j] = \max(dp[j] + 3w,dp[j + v] + 2w,dp[j + 3w]) \]

考虑使用上一道题的方法，提出一个\(3w\)：

\[dp[3v + j] = \max(dp[j],dp[j + v] - w,dp[j + 2v] - 2w,dp[j + 3v] - 3w) \]

这样队列维护的就是\(dp[iv + j] - iw,i \in [0,\min(s,p)]\)

wc太牛逼了

P3423 [POI2005] BAN-Bank Notes

共 \(n\) 种面值的硬币，为 \(b_1,b_2,\cdots,b_n\)。每种硬币有数量限制\(c_i\)，现在我们想要凑出面值 \(m\)，求最少要用多少个硬币

设\(dp[i]\)表示凑出金额\(i\)所需的最小硬币数

转移：\(dp[i] = \min(dp[i - j * b[l]] + j)\)

依照上述思路：维护\(dp[r + kb[i]] - k\)

一定要初始化啊啊啊啊啊啊啊

P2254 [NOI2005] 瑰丽华尔兹

描述略

第一想到理想的正方形

用两个单调队列维护两个维度

但不需要

这道题大抵是要用到\(dp\)的

\(dp[i][j]\)表示走到该格子的最大长

设一个方向上的时间区间长度为\(k\)

则（以向右为例）

\(dp[i][j] = \max(dp[i][l] + j - l + 1),l \in [j - k + 1,j - 1]\)

\(dp[i][j] = \max(dp[i][l] - l) + j + 1,l \in [j - k + 1,j - 1]\)

其他方向从略（向左/向上时，\(l \in[j + 1,j + k - 1]\),所以是\(dp[i][l]/dp[l][i] + l\)，最后\(- j +1\)）

维护：\(dp[i][l] +or- l\)

那就对于每次滑动，用单调队列这个窗口在每一行/列按这个方向滑动，当然会有无效操作，但没关系，因为顺序是对的，最终答案涉及的方格总能按照正确的顺序被修改和记录，所以无所谓，搞就完了

但是：

对于区间\([l,r]\)，\(r - l + 1\)的计算方式包含两个端点，而观察样例可知：每次滑动的起点是不计入答案的

所以操作区间没有加一

方程：

\(dp[i][j] = \max(dp[i][l] + j - l),l \in [j - k + 1,j - 1]\)

\(dp[i][j] = \max(dp[i][l] - l) + j,l \in [j - k + 1,j - 1]\)

踢队头时的区间也是\(|q.front() - l|\)

md坑害我一天

P3089 [USACO13NOV] Pogo-Cow S

有\(N\)个目标点，目标点\(i\)在\(x_i\)，该点得分为\(p_i\)。开始时可以选择站在一个目标点上，只允许朝一个方向跳跃，且每次跳跃的距离大于等于上一次跳跃的距离，并且必须跳到一个目标点，求所经目标点的最大得分和

首先，排序，方向未知，所以向左向各跑一遍

定义\(dp[i][j]\)表示跳到了目标点\(i\)，并且是从\(j\)跳到\(i\)的最大和，得到关系：

\(dp[i][j] = \max(dp[j][k]) + p_i,|x_j - x_k| \leqslant |x_i - x_j|\)

\(dp[i][i] = p_i\)

先以向左为例，向右同理

那么\(0 \leqslant k < j < i \leqslant n\)

暴力是\(O(n^3)\)的，需要优化

肯定优化掉\(k\)那一维

我们采用单调队列的思想，既然已经按位置排了序，那么标号越小的点离\(j\)越远。利用这个天然的单调，从\(j\)开始倒着走找转移点，距离一旦不符合就不找了，节省时间

还有一个大坑：先枚举\(j\)，再枚举\(i\)。

如果不这样，其实相当于默认了起点是\(1\)

观察方程，可知每次转移相当于该方案继承了上一次跳跃的起点，所以必须先锁死起点，再去枚举终点

可见，很多时候单调队列的应用就是单调性的应用，从单调性入手遍历，可以少遍历很多非法情况，有时甚至不用建队，用单调性枚举即可

P2569 [SCOI2010] 股票交易

看到\(AP_i \geqslant BP_i\)，知道了同一天内要么买，要么卖，不可能同时进行（否则必亏）

定义\(dp_{i,j}\)表示第\(i\)天有\(j\)张股票时最多能赚多少

分类讨论：

• 买

  • 在上一次交易的基础上买进
  • 白手起家（这天手头啥也没有）

• 卖

  • 在上一次交易的基础上卖出

• 啥也不干

四大情况，我们来一一分析

• 在上一次交易的基础上买进

\[dp_{i,j} = \max(dp_{i,j},dp_{i - W - 1,j - k} - k \times AP_i),k \in [1,AS_i] \]

• 白手起家：相当于直接赋值

\[dp_{i,j} = -AP_i \times k,k \in[1,AS_i] \]

• 在上一次的基础上卖出

\[dp_{i,j} = \max(dp_{i,j},dp_{i - W - 1,j + k} + k \times BP_i) ,k\in [1,BS_i] \]

• 啥也不干：\(dp_{i,j} = \max(dp_{i,j},dp_{i - 1,j}\))

暴力\(O(T\times MAXP \times \sum (AS_i + BS_i)),\)，三次方级别，70\(pts\)

考虑使用单调队列优化

根据经验，肯定是维护一个\(dp_i + x_i\)的结构，但当前的状态定义没法子这样做（\(j + k,k\)和\(j - k,k\)都不好合并），我们改一下状态，以买进为例:

\[dp_{i,j} = \max(dp_{i,j},dp_{i - W - 1,k} - (j - k) \times AP_i),0 \leqslant j - k \leqslant AS_i \]

\[dp_{i,j} = \max(dp_{i - W - 1,k} + k \times AP_i) - j \times AP_i, \]

此时\(k,k\)对应，括号内的东西在遍历\(j\)时可以使用单调队列维护，以单调性维护队尾，以\(j - k\)的范围维护队头，能压到\(O(T \times MAXP)\)平方级别

可见状态的定义也非常重要 （服了）

2.斜率优化\(dp\)

可以认为是单调队列的拓展方法

观察发现，能用单调队列维护的\(dp\)方程，一定能分离出一个与当前枚举的\(i\)无关的量（单调队列的维护对象），但如果出现了形如\((i - j)^2 = i ^ 2 - 2ij + j ^ 2\)的东西时，\(2ij\)这个东西脚踏双船，\(i\)和\(j\)有一个变了他就变，无法使用普通队列来维护了

那么就针对他来下手

有\(n\)个数，每次取出一段数\([l,r]\)的花费是\((s[r] - s[l - 1])^2 + M\)，\(M\)一定，求最小花费

设\(dp[i]\)表示取完\(1 \sim i\)的最小花费

可得：\(dp[i] = \min(dp[j] + (s[i] - s[j])^2 + M),j \in [1,i)\)

出现了麻烦项，如何处理

我们把式子这样写：

\(dp[i] = \min(dp[j] + s[j]^2 - 2s[i]s[j]) + s[i]^2 + M\)

\(dp[i] = \min(-2s[i](s[j]) + dp[j] + s[j]^2) + s[i]^2 + M\)

发现括号里是一个形如\(kx + b\)的式子，设\(k_i = -2s[i],x_j = s[j],b_j = dp[j] + s[j]^2\)

对于固定的\(i\),\(k_i\)是不变的，变得只有\(x_j,b_j\)，而我们发现这两项只与\(j\)有关，似乎能用队列了

接下来看如何单调

如果想搞单调，即从\(j\)转移比从\(k\)转移更优，那么

\[dp[j] + (s[i] - s[j])^2 + M < dp[k] + (s[i] - s[k])^2 + M \]

化简得：

\[\frac{dp[j] + s[j]^2 - dp[k] - s[k]^2}{s[j] - s[k]} < 2s[i] = -k_i \]

设\(f[x] = dp[x] + s[x]^2\),则

\[\frac{f[j] - f[k]}{s[j] - s[k]} < -k_i \]

看到左边的形式想到小学的直线斜率

那么我们就以\((s[i],f[i])\)为点，代表该处状态

设现在枚举到了\(t\)，有\(i,j,k\)三个备选状态，且状态如下

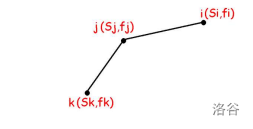
显然

\[\frac{f[j] - f[k]}{s[j] - s[k]} > \frac{f[i] - f[j]}{s[i] - s[j]} \]

对于\(2s[t] = -k_t\)，有以下几种情况

• \(\frac{f[j] - f[k]}{s[j] - s[k]}> \frac{f[i] - f[j]}{s[i] - s[j]}> -k_t\),那么\(j\)比\(i\)优，\(k\)比\(j\)优

• \(\frac{f[j] - f[k]}{s[j] - s[k]}> -k_t > \frac{f[i] - f[j]}{s[i] - s[j]}\)，那么\(i\)比\(j\)优，\(k\)比\(j\)优

• \(-k_t > \frac{f[j] - f[k]}{s[j] - s[k]}>\frac{f[i] - f[j]}{s[i] - s[j]}\)，那么\(i\)比\(j\)优，\(j\)比\(k\)优

也就是说，上凸的点一定不会是最优解，删掉上凸点后，剩下的点一定都往下凸，也就是一个下凸包，即所有线斜率单调不降

接下来，\(-k_t\)已知了，也就说待求直线的斜率已知，那么这根线与凸包最外侧的交点将是转移点（相关详情参考线性规划）

来看看交点的特征

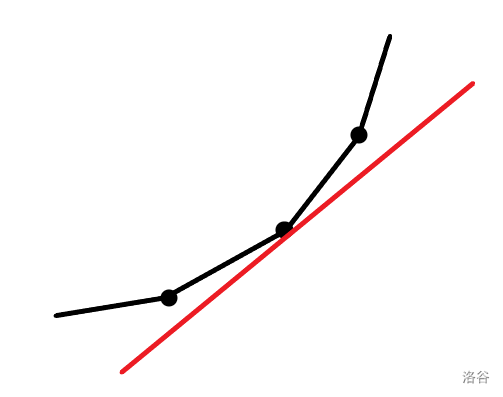
显然，若\(k_a < k_b < \cdots < k_s < -k_t < \cdots\)，则\(s\)点的状态就是转移点

那么用单调队列维护斜率，找到每个\(i\)对应的\(s\)，转移即可

找\(s\)：取出队首的两个元素\(a,b\)，拿推出的式子比，小的为答案，大的就滚蛋

注：先维护队头更答案，再维护队尾塞进\(i\)

P3195 [HNOI2008] 玩具装箱

题目描述

P 教授有编号为 \(1 \cdots n\) 的 \(n\) 件玩具，第 \(i\) 件玩具经过压缩后的一维长度为 \(C_i\)。P 教授不关心容器的数目，他可以制作出任意长度的容器

要求：

• 在一个一维容器中的玩具编号是连续的。

• 如果将第 \(i\) 件玩具到第 \(j\) 个玩具放到一个容器中，那么容器的长度将为 \(x=j-i+\sum\limits_{k=i}^{j}C_k\)。

如果容器长度为 \(x\)，其制作费用为 \((x-L)^2\)。其中 \(L\) 是一个常量。但他希望所有容器的总费用最小。

设\(dp[i]\)表示前\(i\)个玩具装箱的最小代价，那么

\[dp[i] = \min_{0 \leqslant j < i}(dp[j] + (\sum\limits_{k = j + 1}^{i}C_k + i - j - 1 - L)^2) \]

前缀和助阵

\[dp[i] = \min_{0 \leqslant j < i}(dp[j] + (s[i] - s[j] + i - j - 1 - L)^2) \]

再设\(f[i] = s[i] + i\)（可预处理）

\[dp[i] = \min_{0 \leqslant j < i}(dp[j] + (f[i] - f[j] - 1 - L)^2) \]

按鞋油推：

\[\frac{dp_j + (f_j + L + 1)^2 - dp_k - (f_k + L + 1)^2}{f_j - f_k} < 2f_i \]

设\(h_i = dp_i + (f_i + L + 1)^2\)

\[\frac{h_j - h_k}{f_j - f_k} < 2f_i \]

上板子就好了

[APIO2010] 特别行动队

设\(dp_i\)表示\(1 \sim i\)的士兵经修正后的最大战力

那么

\[dp[i] = \max_{0 \leqslant j < i}(dp[j] + a(s[i] - s[j])^2 + b(s[i] - s[j]) + c) \]

再套：

\[\frac{dp_j + as_j^2 - bs_j - (dp_k + as_k^2 -bs_k)}{s_j - s_k} > 2as_i \]

设\(f_i = dp_i + as_i^2 - bs_i\)

\[\frac{f_j - f_k}{s_j - s_k} > 2as_i \]

发现这次是大于号，采用类似的方法，假设是下凸包，发现下凸点是无法成为最优解的，所以这次维护的是上凸包

上板子

P2120 [ZJOI2007] 仓库建设

设\(dp[i]\)表示在\(i\)处建厂的最小费用

对于\(0 \leqslant j < i\)，由定义的状态，可知\(j\)处已经建厂，再结合题目所说，只有\(j + 1 \sim i\)的货物会流入仓库\(i\)，所以

\[dp_i = \min\limits_{0 \leqslant j < i}(dp_j + \sum\limits_{k = j + 1}^{i}p_k(x_i - x_k)) + c_i \]

考虑处理\(\sum\limits_{k = j + 1}^{i}p_k(x_i - x_k)\)

\[\sum\limits_{k = j + 1}^{i}p_k(x_i - x_k) = x_i\sum\limits_{k = j + 1}^{i}p_k - \sum\limits_{k = j + 1}^{i}p_kx_k \]

\(\sum\limits_{k = j + 1}^{i}p_k\)，\(\sum\limits_{k = j + 1}^{i}p_kx_k\)用前缀和处理，记为\(s_i - s_j,t_i - t_j\)

\(dp_i = \min\limits_{0 \leqslant j < i}^{}(dp_j + x_i(s_i - s_j) + t_i - t_j) + c_i\)

\(dp_i = \min\limits_{0 \leqslant j < i}(dp_j - x_is_j - t_j) + x_is_i + t_i + c_i\)

维护\(dp_j - x_is_j-t_j\)

套板子

\[\frac{dp_j - t_j - (dp_k - t_k)}{s_j - s_k} < x_i \]

设\(f_i = dp_i - t_i\)

\[\frac{f_j - f_k}{s_j - s_k} < x_i \]

搞就完了

但这题有一堆细（da）节（bian）：

• 若序列中间存在\(p_i = 0\),会导致除数为零，要\(return\) 极大/极小值来代替

• 中间的工厂没货的话就不可能成为仓库，仓库应该建在最后一个有货的工厂

• 末尾可能会有若干没货的工厂，要从中取一个最小值

淦

P2900 [USACO08MAR] Land Acquisition G

设长为\(x_i,\)宽为\(y_i\)

我们先按\(x\)从小到大排序，再让\(y\)从大到小（保证每次向前枚举的时候符合题意），同时去掉那些被大土地完全包含的小土地

\(dp_i\)表示前\(i\)块土地的最小花费，则

\(dp_i = \min\limits_{1 \leqslant j < i}(dp_j+ x_i \times y_{j + 1})\)

套

\[\frac{dp_j - dp_k}{y_{j + 1} - y_{k + 1}} < - x_i \]

小于号，下凸包？

发现这次的右边成为了一个负数，是单调减的，就好像是这样：

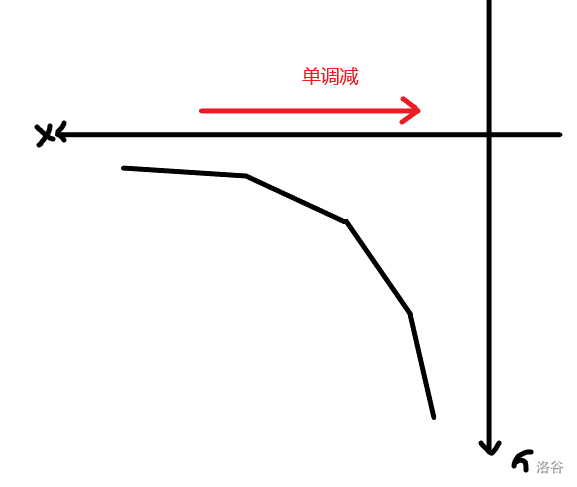
上凸包 （因为6翻了）

可见任何部分的单调性都对凸包是有影响的

还有一点就是队列内元素个数的问题，考虑到一个点就动用了\(k,k + 1\)两个，所以至少留三个（重一个）

P2365 任务安排

设\(dp_i\)表示前\(i\)个任务的最短完成时间

\[dp_i = \min(dp_j + (sumt_i + num \times s) \times (sumf_i - sumf_j)),j \in [0,i - 1] \]

\(sumt,sumf\)为时间，费用的前缀和，\(num\)表示分组数

看到式子里有个\(num\)，考虑把它搞掉（事实上，这个东西不能随着方程转移）

化简式子

\[dp_i = \min(dp_j + sumt_i \times (sumf_i - sumf_j) + num \times s \times (sumf_i - sumf_j)) \]

考虑搞掉\(num\times s \times (sumf_i - sumf_j)\)

根据\(dp\)的尿性，这个\(num\)也不符合\(dp\)的风格（累计），所以考虑对于已知的分组，把该状态分组的影响全部并到此时的方程里一并计算，就可以秒掉\(num\)了

方程中已知的分组就是\(j + 1 \sim i\)

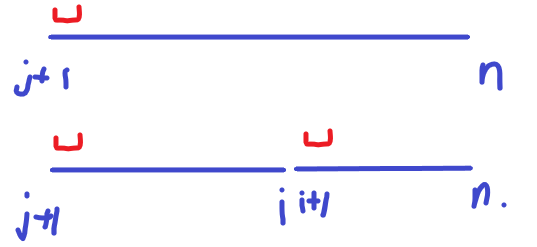
如图明显可得：分组后时间上多了一个\(s\)（\(i+ 1\)处）

代价增加\((sumf_n - sumf_i) \times s\)

但考虑到\(num\)还包含了这一次(\(j + 1\)处)的启动，所以影响其实是

\((sumf_i - sumf_j) * s + (sumf_n - sumf_i) * s = (sumf_n - sumf_j) * s\)

其实就是相对于\(j + 1 \sim n\)不分组（一次也不启动）的增加值

所以

\[dp_i = \min(dp_j + sumt_i \times (sumf_i - sumf_j) + (sumf_n - sumf_j) \times s) \]

\(O(n^2)\),可过弱化版

接下来到了激动人心的优化环节

\[dp_i = \min(dp_j -(sumt_i+s) \times sumf_j) + sumt_i \times sumf_i + sumf_n \times s \]

\(\cdots\)

\[\frac{dp_j - dp_k}{sumf_j - sumf_k} < sumt_i+s \]

下凸包

然后就来了个不要脸的

P5785 [SDOI2012] 任务安排ProMax

\(|T_i| ?\)

wc有负数?

\(sumt\)单调性不存在了！

\(dp\)不变，下凸包不变，麻烦就麻烦在没有单调性

也就是说：

• 弹掉对头的依据没有了

对于第一种情况，我们就不能弹掉队头了，答案也不一定是队头了，要二分查找了

物理学不存在了！(悲伤）（扭曲）（猴叫）（爬行）（蛇了）