树链剖分
看逆天算法，品百味OI#4
1.重链剖分
给出如下定义：
-
重子结点：一个点的子节点中子树最大的点
-
轻子节点：剩余的子节点
-
重边：该节点到重子节点的边
-
轻边：到轻子节点的边
-
重链：若干条首尾相接的重边
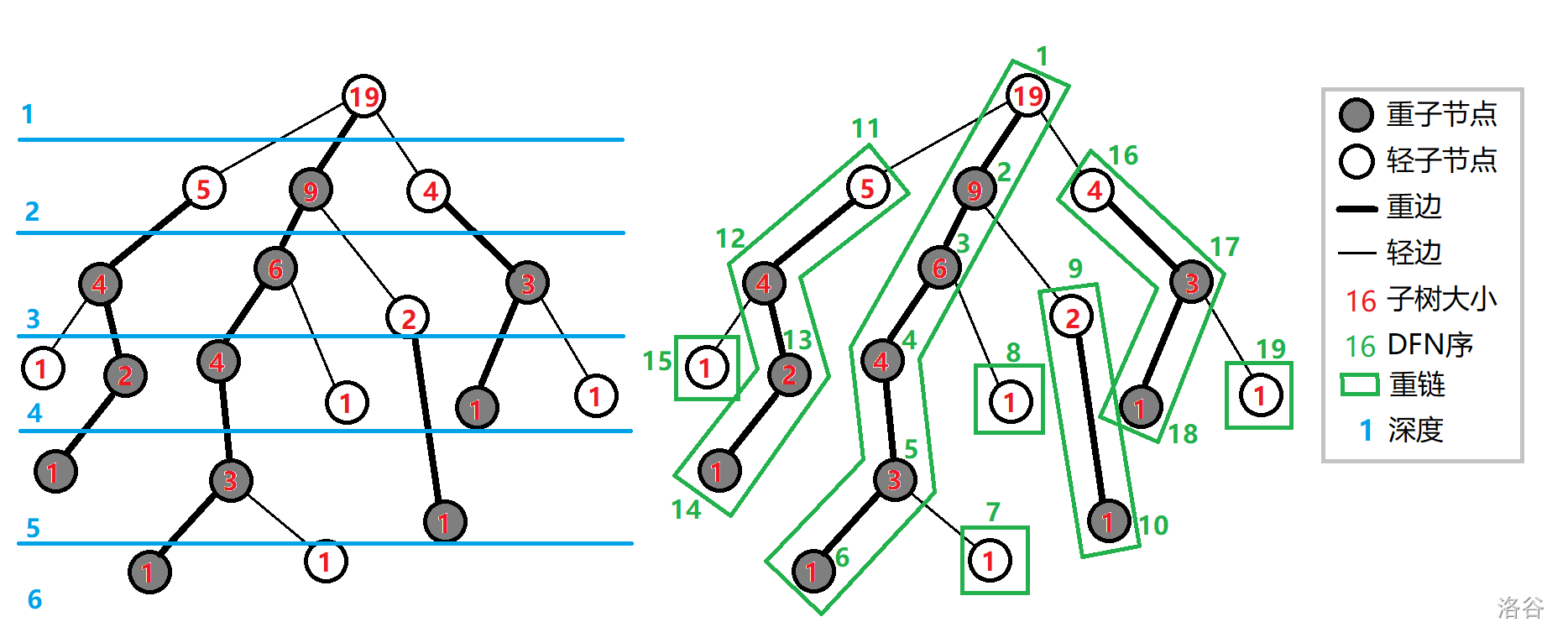
预处理由两个DFS实现
-
DFS1：记录节点的父节点、深度、子树大小、重子结点
-
DFS2：记录所在链的链顶，重边优先遍历时的DFS序、DFS序对应的节点编号
这样之后就可以把树上操作转化为区间操作（重链遍历下\(dfn\)序连续），可以使用线段树或树状数组维护
查询时用到类似\(LCA\)的思想：先把两个点跳到同一条链上，这时可以顺手对经过的区间\([dfn_{fa_x}],dfn_x]\)上来一波操作（求极值，求和等），跳完后再操作\([dfn_x,dfn_y]\)
板子：
P3178 [HAOI2015] 树上操作
「ZJOI 2008」树的统计
QTREE
用到了边权下放（\(dfs\)时实现），这种情况下\(lca\)的值不能纳入查询范围，便有了
ST.query(dfn[x] + 1,dfn[y],1,n,1)
(\(lca\)就是跳到一条链上后深度小的点)
[SDOI2011]染色
合并区间时要特判衔接处是否能合成一个区间，而且正是因为如此，线段树\(query\)的时候如果不跨\(mid\)就分开，只有跨了的时候才判一下，具体而言就是
if(ql > mid) query(ql,qr,mid + 1,r,rs(id));
else if(qr <= mid) query(ql,qr,l,mid,ls(id));
else
{
ans = query(ql,qr,l,mid,ls(id)) + query(ql,qr,mid + 1,r,rs(id));
if(t[ls(id)].rc == t[rs(id)].lc) ans--;
return ans;
}
全是细节
货车运输
没错就是最大生成树那个
原本的\(lca\)同时求\(min\)直接变成树剖后区间求\(min\)，更好想了。码量也大了
运输计划
没错就是那个二分答案后check能否删掉超过答案的\(m\)条路径的边的交集中的边来达到要求的那个，拿lca+差分搞的那个
学了树剖后有了全新大发现
-
沿用二分思路，用树剖求\(lca\),
好像也没啥特别的还加了码量，就lca短了点，优化了常数 -
考虑到树剖的区间操作优势，我们可以直接通过修改那\(m\)条路径来得到答案（正片）
我们选取\(m\)条路径中最长的那条作为标准，记为\(A\)
如果我们删掉了\(A\)中的一条边\(E\)，那么最大值只有两种来源：删掉了边的\(A\)和不经过\(A\)的链中最长的
很好想，过\(E\)的其他路径权值和本来就比\(A\)要小，删了后绝对无优势，反而是那些不受影响的链可能趁机成为最大
这样一来又有重要的一点：删掉不同的边，结果极可能变化
也很好想，删掉不同的\(E\)，不经过\(E\)的路径的集合也不同，变化多样
总结就是：
把\(A\)中的所有边挨个删一遍，对于删掉\(E_i\)后的情况，求删掉了边的\(A\)和不经过\(A\)的路径中最长的路径，记为\(Max_i\)，结果就是\(\min\limits_{E_i \in A}{(Max_i)}\)
对于一条路径，剖分后可以把它拆成若干条链（重/轻链的一部分），设为\((u_i,v_i)\)，共\(k\)个，那么，这些区间的补集就是该路径所不经过的，即\((1,u_1),\cdots (v_{i}+1,u_{i + 1}-1 ),\cdots (v_k,n)\)
对于每一个小段，我们可以预处理出不过这一段的路径中最长的。从而在查询时方便一点
void init(int x,int y,int z)
{
int res = 0;
int fx = top[x],fy = top[y];
// cout << fx << " " << fy << endl;
while(fx != fy)
{
//cout << 114 << endl;;
if(dep[fx] >= dep[fy]) {res++,P[res].c = dfn[fx],P[res].d = dfn[x];x = fa[fx];}
else {res++,P[res].c = dfn[fy],P[res].d = dfn[y];y = fa[fy];}
fx = top[x];fy = top[y];
}
if(dfn[x] > dfn[y]) swap(x,y);
res++;P[res].c = dfn[x] + 1,P[res].d = dfn[y];
sort(P + 1,P + res + 1,cmp);
if(P[1].c > 1) ST.add(1,P[1].c - 1,1,n,1,z);
if(P[res].d < n) ST.add(P[res].d + 1,n,1,n,1,z);
for(int i = 1;i < res;i++)
{
// cout << P[i].d + 1 << " " << P[i + 1].c - 1 << endl;
ST.add(P[i].d + 1,P[i + 1].c - 1,1,n,1,z);
}
//return;
}
时间效率(从高到低)：树剖+ 补集（极限330ms）> 树剖+二分（极限约500ms） > 二分 + 倍增法lca（极限1.12s）
树剖常数真小
遥远的国度
换根问题
-
查询节点就是当前根，查询整个树
-
查询节点不是当前根的祖先，直接查询以该节点为根的子树
-
查询节点是当前根的祖先，这时要按跳链法找到当前节点的儿子\(son\)，那么\([dfn_{son},dfn_{son} + siz_{son} - 1]\)(以该儿子为根的子树)不纳入查询范围，即查询\([1,dfn_{son} - 1] \cup [dfn_{son} + siz_{son},n]\)
找儿子：
int look(int x)
{
if(dfn[x] >= dfn[root] || dfn[x] + siz[x] - 1 < dfn[root]) return 114;
int pos = root;
while(top[pos] != top[x])
{
if(fa[top[pos]] == x) return top[pos];
pos = fa[top[pos]];
}
return hson[x];
}
可以看到，树剖的魅力就是把树转成纯纯的区间，查询某一部分就是对某一区间进行操作，这样就可以用线段树来降复杂度，非常的有实力
