模拟赛总结

//https://images.cnblogs.com/cnblogs_com/blogs/769737/galleries/2232265/o_221024235906_12.jpg
//https://images.cnblogs.com/cnblogs_com/blogs/769737/galleries/2232265/o_221024123148_10.jpg

2024.2.6

T1 珠子

小 F 有 $n $颗珠子排成一个序列，每个珠子有一个颜色，颜色共有 $m $种，编号为 $1,2,…,m $。她想取出一段连续的珠子，对于每一种颜色 \(i\) ，要求取出的珠子个数在\([l_i,r_i] , 0 \leqslant l_i \leqslant r_i \leqslant n\)之间。求有多少种取珠子的方案。

暴力：前缀和处理前\(i\)位第\(j\)类珠子的总数，用\(n^2\)枚举\(l,r\)

期望：\(60pts\)

没用前缀和：\(30pts\)

正解：双指针

先固定左端点，然后分别去找满足颜色要求的最小\(r_1\)(一般是满足下限)和最大\(r_2\)（一般是达到上限），由于\(r_1 \sim r_2\)各颜色数目显然单调不减，所以一对\((r_1,r_2)\)对答案的贡献就是\(r2 - r1 + 1\)

至于怎么较快的找到\(r_1,r_2\)，不会先咕咕

T2 数组

初始\(a_i = i\),现有两种操作

• \(A\)：已知\(p,q\)，修改所有数，\(a_i = p \times i + q\)

• \(B\)：已知\(x,y\)，将\(a_x\)改为\(y\)

给出若干操作，在每次操作后输出数组元素和

第一个好办，看第二种

第二种的麻烦点在于上一次\(x\)位置的\(B\)操作可能会被\(A\)覆盖掉，所以要记录上一次\(A\)操作的时候\(num\)，以及\(x\)处的上一次\(B\)操作的时候\(tag\)

如果\(tag \leqslant num\)，说明上一次的\(B\)操作已经被覆盖掉了，那么就减去上次\(A\)操作改的值，加上\(y\)

否则减去上次\(B\)操作改成的值\(y'\)，加上\(y\)

for(int i = 1;i <= m;i++)
{
	cin >> op;
	if(op == 'A')
	{
		cin >> t[i].p >> t[i].q;
		cnt = i;//记录最新A操作的时候
		sumq = 0;//覆盖掉
		cout << (ll)t[i].p * sum + t[i].q * n << '\n';
	}
	if(op == 'B')
	{
		cin >> t[i].p >> t[i].q;
		if(tag[t[i].p] <= cnt)//上次该处的B已被覆盖
		{
			sumq = sumq + (ll)t[i].q - (ll)(t[cnt].p * t[i].p + t[cnt].q);// 减去A操作留下的值(p*i+q),加上y
			tag[t[i].p] = i;
		}
		else
		{
			int y = tag[t[i].p];
			sumq = sumq + t[i].q - t[y].q;//减去上次B操作留下的值
			tag[t[i].p] = i;
		}
		cout << (ll)t[cnt].p * sum + n * t[cnt].q + sumq << '\n';
	}
}

蒟蒻没有考虑到\(A\)操作会覆盖\(B\)，只得了一半分，gg

T3 幸运区间

已知\(\{a_i\}\)，定义幸运区间为区间内所有数的\(\gcd = 1\),求幸运区间数

暴力：分解质因数，拿质因子搞

\(20pts\)（主要是数组开不了那么多）

正解：双指针(byd)

考虑一个显然的结论：若一个序列存在一个子序列，其所有数的\(\gcd = 1\)，那么这整个序列的数的\(\gcd = 1\)

那么，每次固定左端点，找到最小的\(r\),满足\([l,r]\)中元素\(\gcd = 1\)，那么根据结论：\([l,r],[l,r + 1],[l,r + 2] \cdots [l,n]\)均为幸运区间，也就是说一个\(r\)对答案的贡献\(ans += n - r + 1\)

至于找到最小的\(r\)，可以使用一些数据结构来维护

还有一点：有结论我们还可推得：一个序列的\(\gcd = 1\)，这个序列的子序列的\(\gcd\)一定\(\geqslant1\)，所以找到\(r\)后，我们可以固定\(r\)，跳\(l\)，这样就可以省时间了

int l=1,r=1;
for(l=1;l<=n;l++)
{
	r=max(l,r);//双指针思想，性质保证了可以固定r跳l，这样就是O(n)
	while(l<=r&&r<=n)
	{
		if(st.getgcd(l,r,1,n,1)==1) break;//此处使用线段树，由结论可知gcd有传递性
		r++;
	}
	ans+=n-r+1;
}

T4 找不同

已知一串单词，给定若干区间，判断每个区间中是否有重复单词

先Hash，此处使用map开的mp和last

类比HH的项链，不同单词即不同颜色，那么没有重复就是区间内颜色种类等于区间长度

蒟蒻没想到类比，打的暴力，又gg了，只能说树状数组那章是划水过来的

for(int i = 1;i <= q;i++)
{
	int l1 = b[i].l;
	int r1 = b[i].r;
	while(pos <= r1)
	{
		add(pos,1);
		if(last[mp[pos]] == 0) last[mp[pos]] = pos;//记录上一次出现位置
		else
		{
			if(last[mp[pos]] < pos)//上一次出现位置在区间内
			{
				add(last[mp[pos]],-1);//把原来加的1减掉
				last[mp[pos]] = pos;//更新
			}
		 } 
		 pos++;
	}
	ans[b[i].id].val = sum(r1) - sum(l1 - 1);
	ans[b[i].id].l = l1;
	ans[b[i].id].r = r1;
}

两道双指针题给蒟蒻的第一感觉就是：\(l,r\)只会往一个方向走，不会反向跳到某一位置

2024.2.18

T1 家庭作业

click

设给的数为\(\{a_n\},\{b_m\}\)

对于\((a_i,b_j)\)，它对答案的贡献就是\(\gcd(a_i,b_j)\)

为了防止枚举时重复计算答案，每求完一次\(\gcd\)，就要把求的\(\gcd\)除掉

for(int i = 1;i <= n;i++)
{
	for(int j = 1;j <= m;j++)
	{
		int k = __gcd(a[i],b[j]);
		if(k != 1)
		{
			ans = ans * k % mod;
			a[i] /= k;
			b[j] /= k;//除掉，防止重复
		}
	}
}

硬拿\(\gcd\)搞\(50pts\)，会T掉

本来想到\(O(nm)\)枚举了但没想到怎么避免重复，以为是假的

还是太蒟蒻了

T2 距离之和

click

md调了半天发现是指令数组只开了\(1e5\)

对于一次移动（以向右为例），向右一步，首先不影响\(|\Delta y|\)，那么在出发点左边的控制点到机器人的距离均\(+1\)，在出发点右边的控制点到机器人的距离均\(-1\)，变化量就是两类点的数量差

其他同理

开两个权值线段树（横、纵坐标）统计点个数可过，但是考场上内存炸了直接gg

就挺烦人

其他:

我们可以把坐标排序，用二分找出发点所在分界，这样就免去了桶

//向右
int num = lower_bound(x + 1,x + n + 1,dx + 1) - x;
num = n - num + 1;//lower_bound返回的是第一个不小于dx + 1的数的位置，具体个数要处理一下
int res = n - num;
sum += res - num;//res是左边的点，距离+1，num是右边的点，距离-1
dx++;//更新坐标

或者每次以机器人位置为原点建系，把点划分成在\(x\)轴上/下、在\(y\)轴上/下，在\(x/y\)轴上六个部分以及各行各列的点数

仍以向右为例，此时上下部分不影响，在左边和在\(y\)轴上的点距离+1，在右边的点距离-1，然后更新涉及部分的点的数量

//向右
dx++;
sum += ony + zuo - you;//更新
zuo += ony;//出发点所在列上的点在新Y轴的左边
ony = px[dx];//新y轴上的点
you -= ony;//右边在dy列的点到了坐标轴上，不属于右边

T3 country

click

哈希不用说

（但正解是kmp）

按样例顺序遍历处理有\(10pts\)

听说暴力展开大写字符有\(30pts\)

乱序数据的话要记忆化搜索

坑点在于两个大写代表的串拼起来后可能会生成目标串

首先处理出模式串的\(fail\)指针

\(f_{i,j}\)表示当前匹配到\(i\)号串，匹配指针在\(j\)处的方案数

\(g_{i,j}\)表示把第\(i\)号串匹配完时模式串指针的位置

匹配完\(i\)串后可以直接从\(g_{i,j}\)开始往后来实现拼接大写字母

dfs:

void dfs(int x,int pos)
{
	cout << 114514 << endl;
	if(vis[x][pos]) return;
	int j = pos;
	for(int i = 1;i <= len[x];i++)
	{
		if(a[x][i] >= 'A' && a[x][i] <= 'Z')
		{
			int v = a[x][i] - 'A';
			dfs(v,j);//指针指到了大写字母，直接连着向后匹配 
			f[x][pos] = (f[x][pos] + f[v][j]) % mod;//大写部分的匹配方案数就是f[v][j],dfs后更新答案 
			j = g[v][j];//dfs完了，说明大写字母内部匹配完毕，更新指针 
		}
		else
		{
			while(j && s[j + 1] != a[x][i]) j = fail[j];
			if(s[j + 1] == a[x][i]) j++;
			if(j == m) f[x][pos] = (f[x][pos] + 1) % mod,j = fail[j];
		}//小写字母部分，KMP版子 
	}
	vis[x][pos] = 1;
	g[x][pos] = j;//标记并记录匹配完毕的位置 
}

预处理\(fail:\)

for(int i = 2,j = 0;i <= m;i++)
{
	while(j && s[i] != s[j + 1]) j = fail[j];
	if(s[i] == s[j + 1])j++;
	fail[i] = j;
}//KMP板子预处理fail指针 

T4 太空飞船

click

byd考场上直接想这题想歪了还忘了打暴力保底

暴力\(n^4\)有\(40pts\)

还有一个\(60pts\)的dp，平方级别的，但我写不出来，先看看正解：

容斥原理

采用 “总数-非法的方案” （容斥是不是都爱这么玩）

如果\(\gcd \neq 1\)，说明四个数一定都是某个数的倍数

设\(num_i\)表示\(i\)的倍数的个数

首先，\(2^2,2^3 \cdots\)的倍数一定是\(2\)的倍数，所以\(num_4,num_8\)等都包含在\(num_2\)中，所以我们只需要用所含质数的次数为的\(i\)来搞答案

接下来就是容斥：减掉\(2,3,5\cdots\)的倍数，啊多减了，补上\(2\times 3,2 \times 5\cdots\),啊又加多了，减去\(2\times 3\times 5 \cdots\)

\[\begin{aligned} ans = C_{n}^{4} - C_{num_i}^4 \times (-1)^{cnt} \end{aligned}\]

\(cnt\)就是\(i\)中有多少个质数

还有一点：从质数去枚举不方便，不妨枚举\(1\sim10000\)

for(int i = 1;i <= n;i++)
{
	for(int j = 2;j * j <= a[i];j++)
	{
		if(a[i] % j == 0)
		{
			num[j]++;
			if(j * j != a[i]) num[a[i] / j]++;
		}
	}
}//处理num数组
ans = C[n];//总数
for(int i = 1;i < N;i++)
{
	bool f = 0;
	for(int j = 2;j * j <= i;j++)
	{
		if(i % j == 0 && i / j % j == 0) 
		{
			f = 1;
			break;
		}//如果数的次数超过1
	}
	if(f) continue;
	int cnt = 0;
	int x = i;
	for(int j = 2;j * j <= x;j++)
	{
		if(x % j == 0)
		{
			cnt++;
			while(x % j == 0) x /= j;
		}//统计质数个数
	}
	if(x != 1) cnt++;
	if(cnt % 2 == 1) ans -= C[num[i]];
	else ans += C[num[i]];//容斥
}

2024.2.19

T1 素数

click

md内存又开炸了\(100->0\)啊啊啊啊不对呀我记得开的没那么扯淡呀

欧拉筛出范围内所有素数，拿前缀和\(O(cnt^2)\)搞出各种连续素数和，统计表示数

for(int i = 1;i <= cnt;i++) sum[i] = sum[i - 1] + pri[i];
//cout << sum[cnt] << endl;
for(int i = 1;i <= cnt;i++)
	for(int j = 1;j <= i;j++)
	{
		if(sum[i] - sum[j - 1] > 33000) continue;
		num[sum[i] - sum[j - 1]]++;
	}

我tm考场上怎么开了5e7wc

T2 晨练

click

dp

设\(dp(i,j)\)表示第\(i\)分钟，疲劳度为\(j\)是跑的最大距离

如果选择跑，那就是

\[dp[i + 1][j + 1] = max(dp[i + 1][j + 1],dp[i][j] + d[i + 1]); \]

如果不跑，那么直接休息

坑点：疲劳度为\(0\)后还能继续休息

\[dp[i + j][0] = max(dp[i + j][0],dp[i][j]) \]

\[dp[i + j + 1][0] = max(dp[i + j + 1][0],dp[i + j][0])\text{（从上一分钟的休息状态转移）} \]

初始化:

\[dp[1][1] = d[1]; dp[1][0] = 0 \]

ok,考场上还好从坑里爬出来了

100pts

T3 奇怪的桌子

click

\(20pts:C_{n\times m}^{k}\)

还有十分的小数据，手算的，好像算错了

找规律

考场上想到了一点

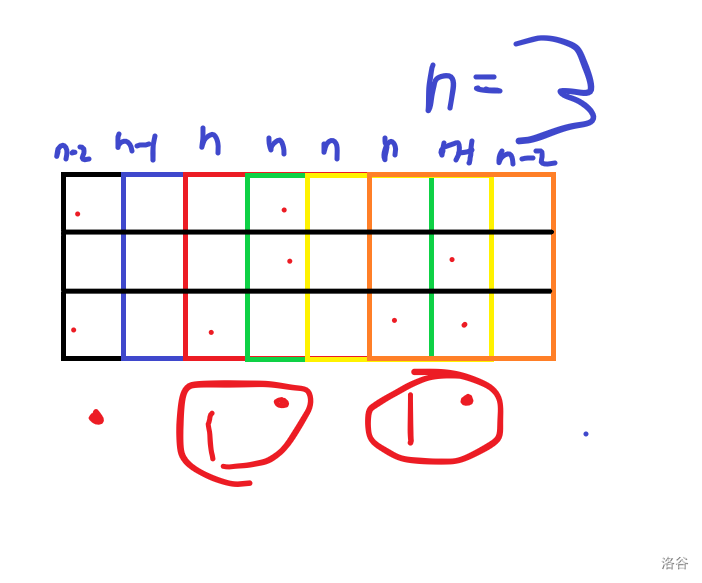
(考试时画的)

有一些列的点数是有规律的（有两个点的是\(1,4,7\)，有一个点的是\(3,6\)）

再看一个一列放三个点的

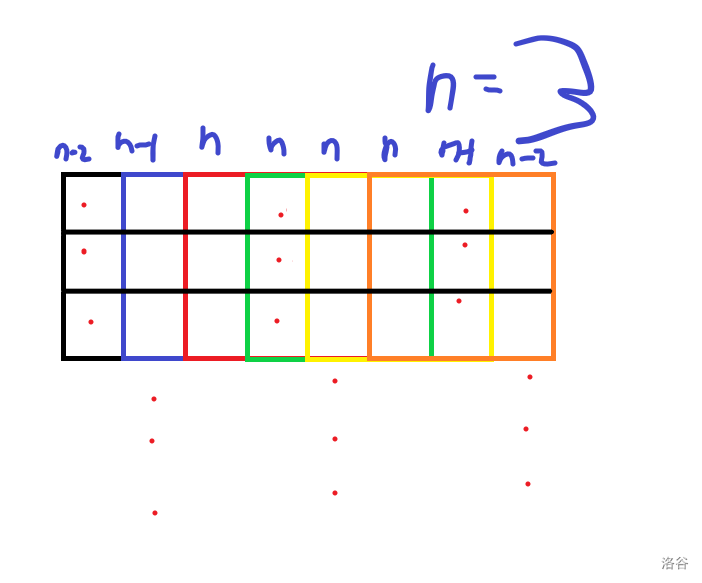
列也有规律，似乎是\(i\%n\)相同

那我们就猜测：

\(i\%n\)相同的列所含点数相同

证明：

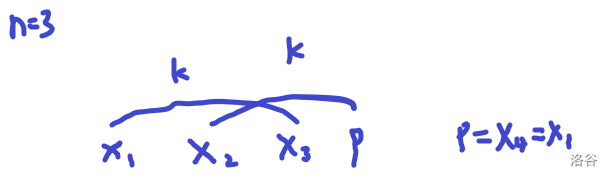
这一点的用处就在于：若某一列有\(j\)个点，那么贡献就是\((C_{n}^{j}) ^ {\lfloor\frac{m}{n}\rfloor}\)

然后dp （啊？）

设\(dp(i,j)\)表示到第\(i\)列，已经放了\(j\)个点

如果我们在当前列要放\(k\)个点，就可以根据规律可得

\(dp(i,j) += dp(i - 1,j - k) \times (C_{n}^{k})^{\lfloor\frac{m}{n}\rfloor+(i <= m\%n)}\)

说明：组合数的指数部分，结合一列三个点的图可以得到。即如果\(i <= m \% n\)，就又包含了一列

但是有一些疑点：

一共\(m\)列，而\(m \leqslant 10^{18}\)

而且上面两幅图的总点数也是不一样的

\(i,j\)的范围又是多少？

？

！

我们观察到对于一种方案，每个正方形内部点的分布是一致的，比如第一张图中，正方形内都是一列\(1\)个，一列\(2\)个，一列没有。第二张图中，正方形内都是仅一列有\(3\)个点

那么我们是不是可以用一个正方形内部的点分布来代替填满整个图，即一种点分布就是一种方案

可以，结合规律，我们就可以用正方形内部的列把其他列推出来

所以只需要dp一个正方形，答案就是\(dp(n,k)\)

for(int i = 1;i <= n;i++)
	for(int j = k - (n - i) * n;j <= k;j++)//这里j的下线意思是：还剩n-i列未填，这里面最多填(n-i)*n个点，那么前面至少填了k-(n-i)*n个点
		for(int l = 0;l <= min(n,j);l++)
			dp[i][j] = (dp[i][j] + dp[i - 1][j - l] * qpow(C(n,l),(m / n + (i <= m % n)) % (mod - 1)))% mod;

还没完

\(k \leqslant N^2\)。循环是个\(O(N^2k)\),还有一个快速幂的log，极限复杂度可达\(O(n^4log)\)，虽然实际上没有这么多，但由于极限过大，实际中还是会\(T\)掉几个点

循环的三次方肯定砍不掉了，那就砍掉log，预处理快速幂

for(int i = 1;i <= n;i++)
	for(int j = 0;j <= max(n,k);j++)
		qp[i][j] = qpow(C(n,j),(m / n + (i <= m % n)) % (mod - 1)) % mod;

T4 学校

click

图的算法忘完了c

HXY算的时间就是最短路耗时

即求断掉某条边后是否还有和原先耗时相同的最短路

每次删边后跑\(dijkstra\)能拿\(30pts\)

由于只考虑最短路，所以可以吧原图中所有最短路（可能不止一条）经过的边提出来建新图，如果在新图中删掉某条边后图不联通，那么删掉这条边就是找不到最短路的

就是\(Tarjan\)中的桥

坑点：有重边

2024.2.21

T1 排序

click

TMD又没开long long

TMD又没开long long

TMD又没开long long

\(100 \to 0\)啊啊啊啊啊啊

正确性（排序不等式）：

若

\[a \geqslant b \geqslant c \geqslant d \]

则

\[ab+cd \geqslant ac+bd\geqslant ad+bc \]

一张图解法（以\(n=3\)为例，实际上\(n\)为多少都一样）

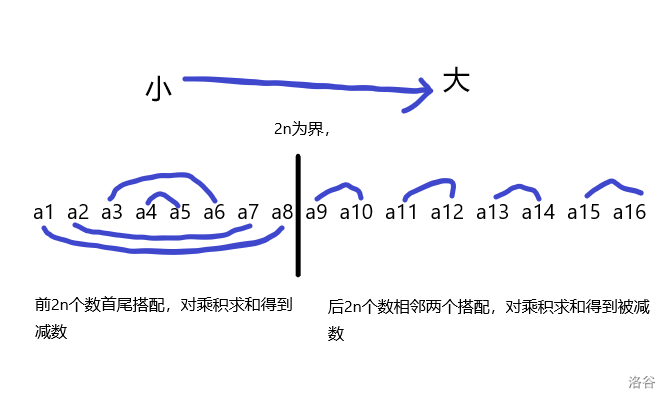
T2 牛吃草

click

想到了二分

二分\(size\)

用类似贪心的方法（肯定是错的）尝试挂分，没想到挂出\(70pts\)

正解还用到了\(dp\)，还是经验不够没想到

设\(f_i\)表示考虑完\([1,i]\)后得到的最大覆盖长度

则

\[f_i = \max\limits_{i - w_i \leqslant j \leqslant i - size}(f_j+(i-j),f_{i-1}) \]

这个暴力式可得\(75pts\)

但也有坑点：\(\max\)函数可能不执行，所以要提前赋上不选情况的值

for(int i = x;i <= n;i++)
{
	dp[i] = dp[i - 1];//跳出坑点
	for(int j = i - w[i];j <= i - x;j++)
	dp[i] = max(dp[i],dp[j] + (i - j));
}

接下来观察到

\[w_{i-1} \geqslant w_i-1 \]

说明

\[(i-1)-w_{i-1}\leqslant (i-1)-(w_{i}-1) = i - w_i \]

下限单调不降，相当于滑动窗口\([i - w_i,i - x]\)，考虑单调队列优化

for(int i = x;i <= n;i++)
{
	//if(i <= w[i]) continue;
	if(w[i] < x)//区间不存在，直接赋值跑路
	{
		dp[i] = dp[i - 1]; 
		continue;
	}
	while(h <= t && dp[i - x] - i + x >= dp[q[t]] - q[t]) t--;
	q[++t] = i - x;
	while(h <= t && i - w[i] > q[h]) h++;
	dp[i] = max(dp[i - 1],dp[q[h]] + (i - q[h]));
}

T3 树上的宝藏

click

想到的是\(n^2\)的树形\(dp\)，但是处理特殊边时出了问题

设\(dp(u,0/1)\)表示不选/选\(u\)时的方案数

具体的，如果一个节点\(u\)与所有儿子的连接中有特殊边，会比较麻烦

但是直接\(dfs\)无法一次得知所有儿子，就可能得到错误的值

这一部分分的题解处理方法很巧妙：断掉特殊边，对形成的两棵子树分别\(dp\)

这样就避免了特殊边的干扰,非常容易的得到\(dp\)方程

\[dp(u,0) = \prod\limits_{v}(dp(v,0)+dp(v,1))\text{ ：不取u，子节点爱取不取} \]

\[dp(u,1) = \prod\limits_{v}dp(v,0)\text{：取了u，由于一定没有特殊边，所以所有子节点都不能取} \]

对于特殊边连接的点\(a,b\)，这俩是至少选一个，答案就是

\[dp(a,0)\times dp(b,1) + dp(a,1)\times dp(b,1) + dp(a,1) \times dp(b,0) \]

初始化：叶子结点不论状态值均为1

for(int j = 1;j <= n;j++) if(in[j] == 1) dp[j][1] = dp[j][0] = 1;
...
void dfs(int x,int fa)
{
	ll ans = 1;
	ll res = 1;
	for(int i = head[x];i;i = e[i].next)
	{
		if(e[i].idx == cut) continue;//模拟断边操作
		int k = e[i].to;
		if(k != fa)
		{
			dfs(k,x);
			ans = (ans * (dp[k][0] + dp[k][1])) % mod;
			res = (res * (dp[k][0])) % mod;//求乘积
		}
	}
	dp[x][0] = ans;
	dp[x][1] = res;
}

\(O(n^2)\)狂炫\(60pts\)

正解太玄乎：

还是先忽略特殊边

设\(g(u,0/1)\)表示不选/选\(u\)时\(u\)子树外部的答案

其实就是选定一条边后需要用到连接点外部的信息

设节点\(u\)的父亲为\(fa\)，一个子节点为\(v\)

我们把\(u\)子树外部分成两部分：\(fa\)的外面和\(fa\)内除了\(u\)的部分

父亲节点的外部就是\(g(fa)\)，抛掉内部子树比较麻烦，以\(v\)节点为例

\[g(v,1) = g(u,0)\times \frac{f(u,0)}{f(v,0)+f(v,1)} \]

抽象？来看图（\(f\)就是暴力\(n^2\)中的\(dp\)）

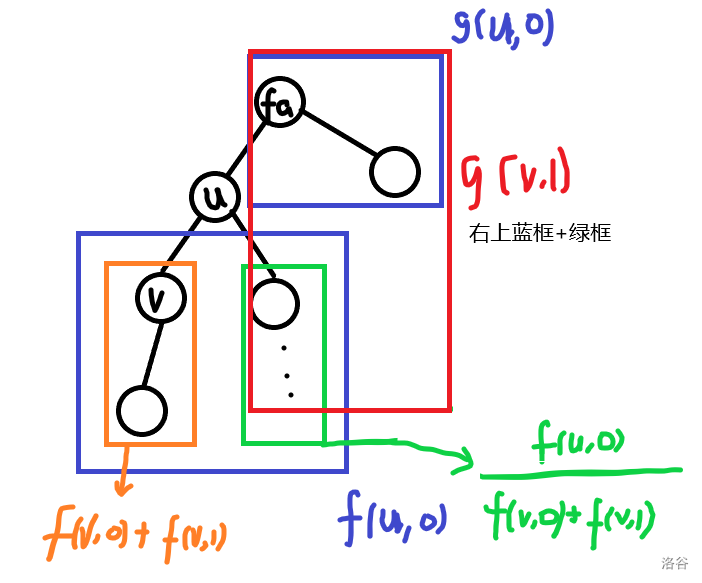
由于不考虑特殊边，所以这里的\(u\)是不选的，图中红框内两部分的综合用的是乘法原理，记得结合\(f\)的求法看，由于\(f\)就是乘积，所以用除法

类似的，可以得到

\[g(v,0) = g(u,0)\times \frac{f(u,0)}{f(v,0) + f(v,1)} + g(u,1) \times \frac{f(u,1)}{f(v,0)} \]

这样求得\(g\)数组后，考虑\(O(1)\)的答案

设特殊边连接的是\(u,v\)（这里\(u\)必须是\(v\)的父亲否则会出锅），则

\[ans_{u,v}=(f(v,1)+f(v,0))\text{（上图中的橙色方框）}\times \frac{f(u,1)}{f(v,0)}\text{（上图中的绿色方框）} \]

\[\times g(u,1)\text{（上图中的右上角蓝色方框）} \]

\[+ f(v,1) \times \frac{f(u,0)}{f(v,1)+f(v,0)}\times g(u,0)\text{（同理不赘述）} \]

\(O(n)\),搞就完了

记得逆元+膜

T4 MEX

click

大毒瘤，暴力一点分没有

假设当前求的MEX为\(k\)，条件显然

• \(0\sim k-1\)都要出现
• \(k\)不出现

枚举右端点，可知区间的左端点也在一个范围内

那么，我们就用\(0\sim k-1\)的位置限制该范围的下界，用\(k\)出现的位置限制该范围的上界。

形式化的就是(\(p_i\)为\(i\)上一次出现的位置)

\[\max{(\min_{i=0}^{k-1}p_i - p_k,0)}\text{（求的是合法左端点的个数 ）} \]

然后再把这个公式改一下

\[\min_{i=0}^{k-1}p_i-\min_{i=0}^{k}p_i \]

对每一个\(k\)，只需求出

\[\sum\min_{i=0}^{k}p_i \]

然后作差就能得到答案

另一种理解：

把问题转化成求MEX\(\leqslant k\)，最后作差得到答案

某区间的MEX\(\leqslant k\)，说明这段区间内存在一个\([0,k]\)未出现

固定左端点，当右端点递增时，该区间的MEX显然单调，说明合法的右端点能组成一个集合，这个集合中的最大值就是\(\max_{i=0}^{k}next_{l,i}-1\text{（next表示从l开始第一个i出现的位置）}\)

使用线段树维护\(\max_{i=0}^{k}next_{l,i}-1\)

由于\(l\)增加只会使得\(next_{l,i}\)增加，则对应的最大右端点也只会增加。而\(l\)右移一位只会使得一个\(next_{l,k}\)改变，那么就相当于对\([k,n]\)取\(max\)

然后就不会了

2024.2.22

T1 打赌

click

找规律

每四列一个周期，分成两部分，右边是不足四列的部分，左边的答案就是\((c/4)\times r \times 14\)

接下来摇一摇色子就可得到：

算就行了

\(100pts\)

T2 舞会

click

方法一：权值线段树维护个数，匹配上一个后删点

删点打标记很麻烦，写炸了，\(only20pts\)

还有写平衡树的

正解：先排序保证单调，然后用类似双指针的方法，对于第\(i\)个男生，找第一个符合条件的女生\(j\)，找到了就\(i++,j++,ans++\)，否则\(j\)一直右移

int l = 1;
int r = n;
while(l <= n && r >= 1 && b[l] < 0 && g[r] > 0)
{
	if(-b[l] > g[r])
	{
		ans++;
		l++;
		r--;
	}
	else r--;
}//男比女高
l = 1,r = n;
while(l <= n && r >= 1 && g[l] < 0 && b[r] > 0)
{
	if(-g[l] > b[r])
	{
		ans++;
		l++;
		r--;
	}
	else r--;
}//女比男高

T3 最小生成树

click

首先，由于一定存在一棵最小生成树，是\(1\sim n\)从小到大连成一条链，每条链的边权为\(1\),而最小生成树边数一定，所以有结论

只有互质的两数之间的边才有可能被保留，否则生成树一定不是最小

想到这里了，然后就想着用组合\(and\)容斥原排除非法情况，没弄出来，废了

看到互质，还可以想到欧拉函数

注意到题目要求父节点标号小于子节点，而\(\varphi(n)\)统计的与\(n\)互质的数均小于\(n\)，那么就相当于节点\(n\)的父亲有\(\varphi(n)\)种

利用乘法原理得到

\[ans = \prod_{i=1}^{n}\varphi(i) \]

T4 买汽水

click

状压暴力有\(30pts\)

正解：折半搜索

直接搜复杂度是\(2^{40}\)会爆掉，剪枝优化能提到\(60pts\)左右，折半搜索就是分成两部分去搜，复杂度降到\(2\times 2^{20}\)，又因为左右两部分互不影响，所以可以排序后用指针合并答案

void dfs1(int x,int sum)
{
	if(x == n / 2 + 1) ans1[++tot] = sum;
	else 
		for(int i = 0;i <= 1;i++)
			dfs1(x + 1,sum + (i?a[x]:0));
}//dfs1(1,0)左半部分
void dfs2(int x,int sum)
{
	if(x == n + 1) ans2[++num] = sum;
	else 
		for(int i = 0;i <= 1;i++)
			dfs2(x + 1,sum + (i?a[x]:0));
}//dfs2(n / 2 + 1,0)右半部分
int l = 1;
	int r = num;
	ll ans = -1;
	while(l <= tot && r)
	{
		while(ans1[l] + ans2[r] > m) r--;//找到第一个符合条件的r
		if(r) ans = max(ans,ans1[l] + ans2[r]);
		l++;//排序后这样做只会使和增加，所以不用动右指针
	}

2024.3.10

T1 [USACO09MAR] Cow Frisbee Team S

click

\(01\)背包求方案数

十来分钟打了个板子小代码就溜了

结果不出意外的出意外了——T了，\(40pts\)

int n,f;
int a[N];
map<ll,int> dp;
int sum = 0;
int main()
{
	scanf("%d%d",&n,&f);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]),sum += a[i]; 
	dp[0] = 1;
	for(int i = 1;i <= n;i++)
	{
		for(int j = sum;j >= a[i];j--)
		{
			dp[j] = (dp[j] + dp[j - a[i]]) % mod;
		}
	}
	ll ans = 0;
	for(int i = f;i <= sum;i += f)
		ans = (ans + dp[i]) % mod;
	printf("%d",ans);
	return 0;
}

后来经wzw奆神点拨才发现：

所以他要求队伍的总能力必须是
\(F\)的倍数

这不是排列的trick吗？

所以把上面代码滚掉的一维（第几个）拿回来，开第二维表示余数，余数那一维走背包操作，答案就是\(dp_{n,0}\)

for(int i = 1;i <= n;i++) scanf("%d",&a[i]),dp[i][a[i] % f] = 1;//初始化
for(int i = 1;i <= n;i++)
{
	for(int j = 0;j < f;j++)
	{
		dp[i][j] = (dp[i][j] + dp[i - 1][j]) % mod;
		dp[i][j] = (dp[i][j] + dp[i - 1][((j - a[i]) % f + f) % f]) % mod;//内部取余操作是为了防止出现负数
	}
}
printf("%d",dp[n][0]);

T2 Prufer 序列多源生成树

click

标题党

还以为是\(Prufer\)，当场吓傻了，\(10\)秒走人：

printf("1");

wc\(60pts\)

正解是什么树的直径，用搜索就行

题意要求在保证深度最小的情况下最小化根的编号

保证树的深度最小，可以计算树的直径并取得最小，在保证直径最小下令编号最小，用树上\(DFS/BFS\)，也可以用树形\(dp\)

//树形dp求直径
//dp[i]：以i为根的子树中最长路径长度 
//g[i]:以i为根的子树中次长路径的长度
//id[i]:i对应的最长路径端点 
void dfs1(int x,int fa)
{
	for(int i = head[x];i;i = e[i].next)
	{
		int k = e[i].to;
		if(k == fa) continue;
		dfs1(k,x);
		if(dp[x] < dp[k] + 1)
		{
			g[x] = dp[x];
			dp[x] = dp[k] + 1;
			id[x] = k;
		}
		else if(g[x] < dp[k] + 1) g[x] = dp[k] + 1;
	}
}
//合并找直径 
void dfs2(int x,int fa)
{
	d[x] = d[fa] + 1;
	if(x == id[fa]) d[x] = max(d[x],g[fa] + 1);
	else d[x] = max(d[x],dp[fa] + 1);
	for(int i = head[x];i;i = e[i].next)
	{
		int k = e[i].to;
		if(k != fa) dfs2(k,x);
	}
	dp[x] = max(dp[x],d[x]);
}
int main()
{
	int n;
	scanf("%d",&n);
	for(int i = 1;i <= n - 1;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
		add(v,u); 
	}
	//printf("1");
	dfs1(1,0);
	dfs2(1,0);
	int ans = 1;
	for(int i = 1;i <= n;i++)//从小号开始枚举
		if(dp[ans] > dp[i]) ans = i;
	printf("%d",ans); 

T3 P3216 [HNOI2011] 数学作业

click

前\(30pts\)很好来：暴力\(O(n)\)

ll check(ll x)
{
	if(1 <= x && x <= 9) return 10;
	if(10 <= x && x <= 99) return 100;
	if(100 <= x && x <= 999) return 1000;
	if(1000 <= x && x <= 9999) return 10000;
	if(10000 <= x && x <= 99999) return 100000;
	if(100000 <= x && x <= 999999) return 1000000;
	if(1000000 <= x && x <= 9999999) return 10000000;
}
int main()
{
	ll n,mod;
	scanf("%lld%lld",&n,&mod);
	ll ans = 0;
	for(int i = 1;i <= n;i++)
	{
		ans = (ll)(ans * check(i) % mod + i % mod) % mod;//递推
	}
	printf("%lld",ans);
	return 0;
}

上面的代码很暴力，但是有一点值得肯定：

找到了递推式，也就是\(dp\)

\[dp_{i} = (dp_{i - 1} \times 10^{num} + i) \% mod \]

\[num是i的位数 \]

\(n \leqslant 10^{18}\)，肯定需要\(log\)级别的加速方法

还是优化\(dp\)，指向很明显了

矩阵快速幂

先用\(dp\)式构出矩阵雏形

\(\begin{bmatrix}dp_i \\\\\\\end{bmatrix} = \begin{bmatrix}10^{num} & 1 & &\\\\\\\end{bmatrix}\times \begin{bmatrix}dp_{i - 1} \\i\\\\\end{bmatrix}\)

完善

\(\begin{bmatrix}dp_i \\dp_{i+ 1}\\\\\end{bmatrix} = \begin{bmatrix}10^{num} & 1 & 0\\\\\\\end{bmatrix}\times \begin{bmatrix}dp_{i - 1} \\i\\\\\end{bmatrix}\)

\(\begin{bmatrix}dp_i \\i+ 1\\1\\\end{bmatrix} = \begin{bmatrix}10^{num} & 1 & 0\\0&1&1\\0&0&1\end{bmatrix}\times \begin{bmatrix}dp_{i - 1} \\i\\1\end{bmatrix}\)

递归

\(\begin{bmatrix}dp_n \\n+ 1\\1\\\end{bmatrix} = \begin{bmatrix}10^{num} & 1 & 0\\0&1&1\\0&0&1\end{bmatrix}^ n\times \begin{bmatrix}dp_{0} \\1\\1\end{bmatrix}\)

这里\(num\)会随着数的位数变化，所以要对\(num\)相同的区间做快速幂，然后跨区间时变一下\(num\)

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,mod;
ll ten[20];
struct ma
{
	ll m[5][5];
}ans,base;
ma cal(ma a,ma b)
{
	ma tmp;
	for(int i = 1;i <= 3;i++)
	{
		for(int j = 1;j <= 3;j++)
		{
			tmp.m[i][j] = 0;
			for(int k = 1;k <= 3;k++) tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] % mod * b.m[k][j] % mod) % mod,tmp.m[i][j] = (tmp.m[i][j] % mod + mod) % mod;
			//cout << tmp.m[1][1] << endl;
		}
	}
	return tmp;
}
void init(int num)
{
	ans.m[1][1] = ten[num] % mod;//记得取模
	ans.m[1][2] = ans.m[2][2] = ans.m[2][3] = ans.m[3][3] = 1;
	ans.m[1][3] = ans.m[2][1] = ans.m[3][1] = ans.m[3][2] = 0;
	/*for(int i = 1;i <= 3;i++)
	{
		for(int j = 1;j <= 3;j++)
			cout << ans.m[i][j] << " ";
		cout << endl;
	}*/
}//预处理左上角10的num次方
ma qpow(ll num,ll ci)
{
	init(num);
	base = ans;
	while(ci)
	{
		if(ci & 1) ans = cal(ans,base);
		base = cal(base,base);
		ci >>= 1;
	}
	return ans;
}
int main()
{
	scanf("%lld%lld",&n,&mod);
	ten[0] = 1;
	for(int i = 1;i <= 18;i++) ten[i] = ten[i - 1] * 10;//10的若干次方
	int cnt = 0;
	ll x = n;
	while(x)
	{
		x /= 10;
		cnt++;
	}/最大位数
	//cout << cnt << endl;
	ma A;
	A.m[1][1] = 0;
	A.m[2][1] = 1;
	A.m[3][1] = 1;
	ma B;
	B = qpow(1,8);
	A = cal(B,A);//dp[0] ~ dp[9]
	//cout << A.m[3][1] << endl;
	for(int i = 2;i < cnt;i++)
	{
		B = qpow(i,9 * ten[i - 1] - 1);//9-99是90次，99-999是900次，以此类推
		A = cal(B,A);
	}//分区间处理
	B = qpow(cnt,n - (ten[cnt - 1] - 1) - 1);//10的某次方到n
	A = cal(B,A);//一定要尺寸对应，cal(A,B)就是错的
	printf("%lld",A.m[1][1]);
	return 0;
}

T4 P6239 [JXOI2012] 奇怪的道路

click

状压\(dp\)，做对一半

维数定义的差不多，设\(dp_{i,S,j}\)表示当前在点\(i\)，\(i\)与\(i-k\sim i + k\)的连接状态是\(S\)，用了\(j\)条边

但这样开数组直接\(RE\)了

后来发现：当前城市往后连（连标号比他大的）等价于后面的往前连（大编号连小编号），反之亦然。所以连的城市只需要考虑我原先想的那个区间的一半，这样的话空间也节约不少

再后来发现第二维状态需要修改，具体的，还是因为按原定义的话连的边的数量难以保证（我们只能从状态得知连没连），所以改进为 \(i-k\sim i\) 这些点的度数的奇偶性，\(1\)为奇数，\(0\)为偶数

这样一来， \(dp_i\)和\(dp_{i+ 1}\)的区间又有重叠，梦回动物园

由于一对城市之间可以连若干条边，所以现在\(dp_{i}\)中间转移完（枚举\(j\)和\(S\)），再在\(dp_i,dp_{i + 1}\)之间转移

由于区间重叠，所以直接

\[dp_{i + 1,S << 1,j} += dp_{i,S,j} \]

对于\(dp_i\)内部的转移，我们每次加一条边，每新加一条边，肯定会改变两个点的状态，其中一个点就是\(i\)，因为前\(i-1\)个点连好了，另一个点\(\in [i - k,i - 1]\)，要枚举

改变奇偶的话，\(1 \to 0,0 \to 1\)，想到异或

坑点：\(i - k\)可能小于\(0\)，要和\(1\)比\(\max\)，不然\(30pts\)

#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
int n,m,k;
int dp[35][2050][35];
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	dp[2][0][0] = 1;//1 - 1 = 0无意义，直接从2开始
	for(int i = 2;i <= n;i++)
	{
		int minn = max(1,i - k);//得有
		for(int j = minn;j <= i - 1;j++)//枚举新增边的一个端点，另一端是i 
		{
			for(int v = 1;v <= m;v++)
			{
				for(int s = 0;s <= (1 << (k + 1)) - 1;s++)
				{
					dp[i][s][v] = (dp[i][s][v] + dp[i][s ^ (1 << i - j) ^ 1][v - 1]) % mod;
				}//i - j为枚举的点相对于最右端的位置，i的位置就是i - i = 0,所以是 1 << 0 = 1
			}
		}
		for(int j = 0;j <= m;j++)
		{
			for(int s = 0;s <= (1 << k) - 1;s++)
			{
				dp[i + 1][s << 1][j] = (dp[i + 1][s << 1][j] + dp[i][s][j]) % mod;
			}//区间平移
		}	
	}
	printf("%d",dp[n][0][m]);//答案就是点的度数都是偶数
	return 0;
}

2024.3.24

cnm怎么全是数学cccc

T1 卫星照片

click

\(bfs\)染色，得到左上角和右下角，进而得出矩阵大小，暴力检索内部有没有别的，就完了，\(100pts\)

#include<bits/stdc++.h>
#define N 80
using namespace std;
int r,c;
char a[N][N];
int vis[N][N];
int cow,house;
int dx[5] = {0,0,0,1,-1};
int dy[5] = {0,1,-1,0,0};
int maxx,minx,maxy,miny;
int chang,kuan;
struct node
{
	int x,y;
};
queue<node> q;
void bfs(int u,int v)
{
	maxx = minx = u;
	maxy = miny = v;
	q.push({u,v});
	vis[u][v] = 1;
	while(!q.empty())
	{
		node tmp = q.front();
		q.pop();
		for(int i = 1;i <= 4;i++)
		{
			int nx = tmp.x + dx[i];
			int ny = tmp.y + dy[i];
			if(!vis[nx][ny] && nx >= 1 && nx <= r && ny >= 1 && ny <= c && a[nx][ny] == '#')
			{
				vis[nx][ny] = 1;
				q.push({nx,ny});
				maxx = max(maxx,nx),minx = min(minx,nx);
				maxy = max(maxy,ny),miny = min(miny,ny);//bfs时求矩形的角
			}
		}
	}
	chang = maxx - minx + 1;
	kuan = maxy - miny + 1;//矩阵大小
}
bool check(int k,int s)
{
	for(int i = k;i <= k + chang - 1;i++)
		for(int j = s;j <= s + kuan - 1;j++)
			if(a[i][j] != '#') return 0;
	return 1;
}//判断是房子还是牛群
int main()
{
	scanf("%d%d",&r,&c);
	for(int i = 1;i <= r;i++)
		for(int j = 1;j <= c;j++)
			cin >> a[i][j];
	for(int i = 1;i <= r;i++)
	{
		for(int j = 1;j <= c;j++)
		{
			if(!vis[i][j] && a[i][j] == '#')
			{
				chang = kuan = 0;
				bfs(i,j);if(!check(i,j)) cow++;
				else house++;
			}
		}
	}
	printf("%d\n%d",house,cow);
	return 0;
}

T2 小魔女帕琪

click

乏了，被这道题爆杀

做期望做多了以为是\(dp\)，然后看到\(10^9\)又TM想到矩快加速，然后发现一维\(dp\)不够用，又写了二维乱搞搞不出来，最后才意识到是数学推结论题。。。。。。

想起了被列队春游支配的恐惧c

记\(\sum a_i = n\)，即一共能施法多少次

注意到期望中权值乘的概率是一样的：\(\frac{1}{n!}\)

所以只需要求出权值和

一个施法区间权值为1，那就是求总方案数

首先，一个施法区间排列数为\(7!\)

其次，考虑分布位置，这点和列队春游如出一辙，可以得到共\(n - 6\)种分布

再让剩下位置自由排列造不同方案，共\((n-7)!\)种

还有一点：区间内第\(i\)种魔法只释放一次，而一共有\(a_i\)个\(i\)，所以一个区间由所有晶石释放的方案数是\(\prod a_i\)

那么

\[ans = \frac{7!(n-6)(n-7)!\prod a_i}{n!} \]

化简可得

\[ans = \frac{7!\prod a_i}{(n-5)(n-4)(n-3)(n-2)(n-1)n} \]

md

T3 魔法阵

click

拿条件卡枚举范围的题

设一个魔法阵的值分别为\(A,B,C,D\)

最暴力是\(m^4\)，等式可以拿来算\(B\)，压到\(m^3\)可以水\(70\)，但是炸了

for(int i = 1;i <= m;i++) scanf("%d",&a[i].val),a[i].id = i,cnt[a[i].val].push_back(i);
sort(a + 1,a + m + 1,cmp);
for(int i = 1;i <= m;i++)
{
	for(int j = i + 1;j <= m;j++)
	{
		for(int k = j + 1;k <= m;k++)
		{
			int A = a[i].val;
			int C = a[j].val;
			int D = a[k].val;
			int B = A + 2 * (D - C);
			if(A < B && B < C && C < D)
			{
				if(cnt[B].size() == 0) continue;
				if(3 * A + C > 4 * B)
				{
					for(int l = 0;l < cnt[B].size();l++) 
					{
						num[a[i].id].a++;
						num[a[j].id].c++;
						num[a[k].id].d++;//这三条当时放到循环外面了，没有和B个数同步，就炸了
						int h = cnt[B][l];
						num[h].b++;
					}
				}
			}
		}
	}
}

现在考虑优化

事实上，上面的优化有一步可以借鉴：使用桶存储出现次数

那么，我们就尝试把所有物品都分到桶里，到时候直接枚举权值而不是具体的哪一个

那么就要讨论枚举的权值的取值范围

我们把等式带入不等式：

\[6(D-C)<C-B \]

设\(t = D -C\)，那么

\[6t = C - B \]

\[B - A = 2t \]

设\(6t+k = C - B\)，那么可得到

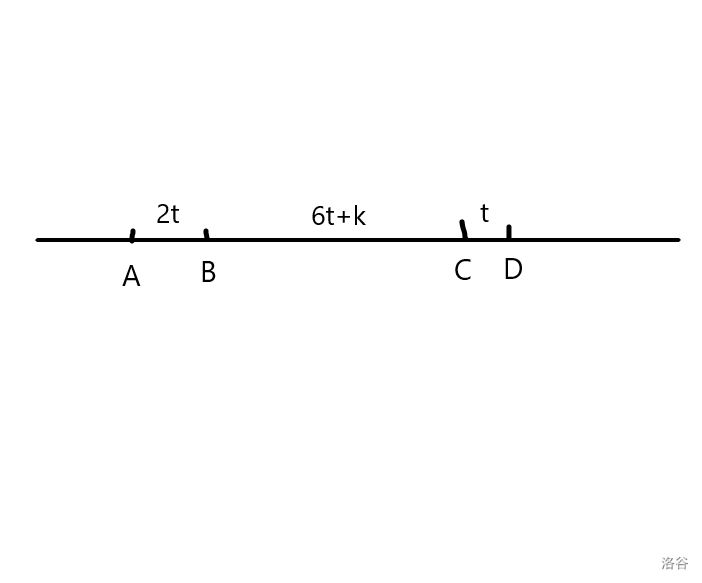
最大差值达到了\(9t+k\)，说明\(9t < n\)，可以枚举\(t\)

枚举\(D\)，我们可以得到\(C = D - t\)，考虑不同的\(A,B\)做出的贡献

显然，只要保证图中的相对关系不变即可形成魔法阵，那么，不妨令\(k = 1\)，那么\(6t+1\)就是一个最小单元，那么当\(C,D\)后移时，先前的\(A,B\)依旧合法，可以使用前缀和

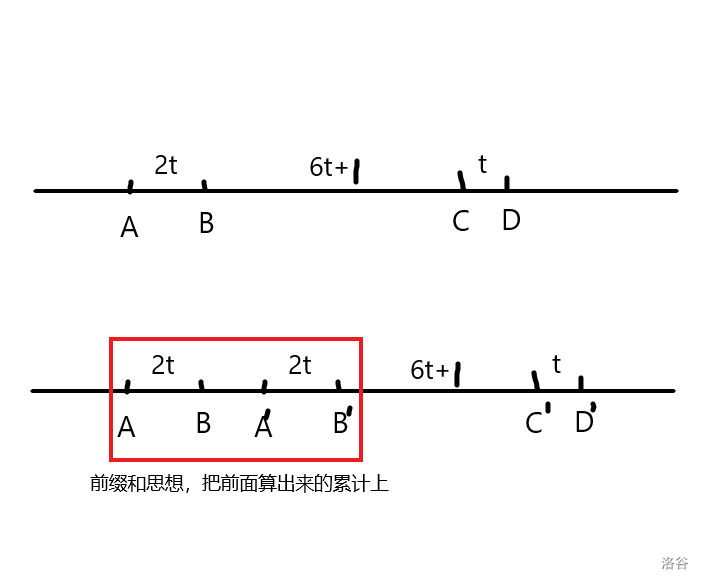
每一对\(A,B\)的贡献都是\(num_A \times num_B\)，\(num\)表示该权值的数量，再乘以\(num_C,num_D\)即可求出\(c,d\)

求\(a,b\)同理，但是要倒序

这逆天思路是我不配

//这里由于枚举的都是权值，所以a/b/c/d[i]表示当权值为i时对应的a/b/c/d的值
for(int t = 1;t * 9 < n;t++)
{
	int sum = 0;
	for(int D = 9 * t + 1;D <= n;D++)
	{
		int C = D - t;
		int B = C - 6 * t - 1;
		int A = B - 2 * t;
		sum += tong[A] * tong[B];//前缀和累加
		c[C] += sum * tong[D];//计算方案数
		d[D] += sum * tong[C];
	}
	sum = 0;
	for(int A = n - 9 * t - 1;A >= 1;A--)
	{
		int B = A + 2 * t;
		int C = B + 6 * t + 1;
		int D = C + t;
		sum += tong[C] * tong[D];
		a[A] += tong[B] * sum;
		b[B] += tong[C] * sum; 
	}
}

T4 [HAOI2016] 字符合并

click

考场上题都没看懂

\(k \leqslant 8\)，状压？

又是区间合并状物，区间\(dp\)?

囊括要素法定义\(dp\):设\(dp_{i,j,S}\)分别囊括左右端点（区间要素）和状态（状压要素）

接着细化含义：\(dp_{i,j,S}\)表示区间\([i,j]\)合并的最高权值，合并后（合并到不能再合并）的状态为\(S\)

采用区间的\([i,l],[l + 1,j]\)法，枚举断点，那么\([i,j]\)就是\([i ,l],[l+1,j]\)的方案和

不妨设定\([l+1,j]\)的长度就是\(k\),考虑到任意长为\(k\)的区间合并后不是\(0\)就是\(1\)，那么合并完后半部分的区间后的新状态不是\(S << 1\)（尾巴多个0）就是\(S << 1 | 1\)（尾巴多个1）

那么可以写出方程

\[dp_{i,j,S << 1} = \max(dp_{i,l,S} + dp_{l + 1,j,0}) \]

\[dp_{i,j,S << 1 | 1} = \max(dp_{i,l,S} + dp_{l + 1,j,1}) \]

接下来关于初始化和特殊情况：

\(dp_{i,i,a_i} = 0\)，最小区间合并结果就是他自己，不需代价

重点来了：有些区间合并若干次后长度正好为\(k\)，那么只需要合并一次，不再枚举断点

我们考虑一下这样的区间的长度有什么性质

每次合并相当于砍掉\(k\)个补上\(1\)个，长度减少了\(k-1\)，那么最后的长度为\(k\)，就满足\(Len = x(k - 1) + k\)，再写一下就是\(Len = x(k - 1) + 1\)

那么对于这种区间，加的权值就是\(w_S\)，对应留下的就是\(c_S\),

\[dp_{i,j,c_s} = \max(dp_{i,j,S} + w_S) \]

接下来是超级细节环节

• 断点枚举

由于合并的区间不重叠，那么每次就要跳过已合并的部分

l -= (k - 1)

• 状态的枚举

就是

for(int l = j - 1;l >= i;l -= (k - 1))
{
	for(int s = 0;s <= ?;s++)
	{
		dp[i][j][s << 1] = max(dp[i][j][s << 1],dp[i][l][s] + dp[l + 1][j][0]);
		dp[i][j][s << 1 | 1] = max(dp[i][j][s << 1 | 1],dp[i][l][s] + dp[l + 1][j][1]);
	}
}

当\(Len < k\)时就没必要跑到\(2^k-1\)，跑到\(2^{len}-1\)即可，注意这里的\(len\)是剩下的合并不了的，也就是对\(k-1\)求余过的，这里模数为\(0\)时要改成\(k-1\)不然会炸循环

int r = 余数; 
if(r == 0) r = k - 1;
for(int l = j - 1;l >= i;l -= (k - 1))
{
	for(int s = 0;s <= (1 << r) - 1;s++)
	{
		dp[i][j][s << 1] = max(dp[i][j][s << 1],dp[i][l][s] + dp[l + 1][j][0]);
		dp[i][j][s << 1 | 1] = max(dp[i][j][s << 1 | 1],dp[i][l][s] + dp[l + 1][j][1]);
	}
}

此时进行的是一个初始化操作（把一些极小值变成\(0\)），这一点会影响求余方式的选择

• 求余

进入特别\(dp\)的条件是\(mod (k - 1) = 1\)，那么就衍生出了两种方法(其中\(if:r = 0,则r = k - 1\))

\[r = len \% (k-1),if(r == 1) ... \]

\[r = (len - 1) \% (k-1),if(r == k - 1)... \]

选择哪一种呢？

特殊\(dp\)中的状态是\(0\sim 2 ^ k - 1\)，所以\(0\sim 2^{k-1}\)都要初始化掉，即\(r = k - 1\)

显然是第二种求余方式

• 特殊\(dp\)

这里不能直接按照\(dp\)式来写，会\(65pts\)，要开临时数组，因为\(S\)会枚举到\(0,1\)，导致用\(dp_{i,j,0/1}\)更新\(dp_{i,j,1/0}\)，肯定不对

复杂度大概是个\(O(n^22^k)\)

for(int i = 1;i <= n;i++)
	for(int j = 1;j <= n;j++)
		for(int s = 0;s <= (1 << k);s++) dp[i][j][s] = -inf;
for(int i = 1;i <= n;i++) dp[i][i][a[i]] = 0;
for(int len = 2;len <= n;len++)
{
	for(int i = 1;i + len - 1 <= n;i++)
	{
		int j = i + len - 1;
		int r = (len - 1) % (k - 1); 
		if(r == 0) r = k - 1;
		for(int l = j - 1;l >= i;l -= (k - 1))
		{
			for(int s = 0;s <= (1 << r) - 1;s++)
			{
				dp[i][j][s << 1] = max(dp[i][j][s << 1],dp[i][l][s] + dp[l + 1][j][0]);
				dp[i][j][s << 1 | 1] = max(dp[i][j][s << 1 | 1],dp[i][l][s] + dp[l + 1][j][1]);
			}
		}
		if(r == k - 1)
		{
			maxx[0] = maxx[1] = -inf;
			for(int s = 0;s <= (1 << k) - 1;s++) 
			{
				maxx[c[s]] = max(maxx[c[s]],dp[i][j][s] + w[s]);
				dp[i][j][0] = maxx[0];dp[i][j][1] = maxx[1];
			}
		}
	}
}
ll ans = -inf;
for(int s = 0;s <= (1 << k) - 1;s++)
	ans = max(ans,dp[1][n][s]);

2024.4.5

今天没带脑子，不知道为啥老想睡，再加上题不好搞，就gg了

后两道题完全跟概率和期望没啥关系，顶多就是做个除法，T3组合，T4数据结构（听说优化暴力也行）

P4550 收集邮票

click

还算正经考期望的

看形式想到Jon and Orbs，然后就被带偏到二维\(dp\)上去了，没救了

其实后来想想也确实不一样，那道题次数题目说了是收敛的，所以可以范围搞大点，这题次数没说有啥性质，得维护

然后倒序（取了\(i\)种，取完剩下的）

设从\(i\)张到\(n\)张要\(k_i\)步（不是期望）

对于次数，有\(\frac{i}{n}\)的概率取到同一种，剩下的概率取到新的

\[g_i = E(k_i) = \frac{i}{n}g_i+ \frac{n - i}{n}g_{i+1}+1 \]

对于价格，结合每次的价格等于是第几次，由期望原始定义

\[ans_i = E(\frac{k_i(k_i + 1)}{2}) = E(\frac{k_i^2 + k_i}{2}) = \frac{E(k_i^2) + E(k_i)}{} \]

设\(h_i = E(k_i^2)\)

因为

\[E((k_i + 1)^2) = E(k_i ^2 + 2k_i + 1) = E(k_i^2) + 2E(k_i) + 1 \]

再结合有\(\frac{i}{n}\)的概率抽到旧的，剩余概率抽到新的，所以

\[h_i=\frac{i}{n}E((k_i+1)^2 ) + \frac{n-i}{n}E( (k_{i+1}+1)^2 ) = \frac{i}{n}(h_i + 2g_i + 1) + \frac{n-i}{n}(h_{i+1} + 2g_{i+1} + 1) \]

答案就是\(ans_0 = \frac{h_0 + g_0}{2}\)

for(int i = n - 1;i >= 0;i--)
{
	g[i] = g[i + 1] + n * 1.0 / (n - i);
	h[i] = ((2 * g[i] + 1) * i * 1.0 / n + (h[i + 1] + 2 * g[i + 1] + 1) * (n - i) * 1.0 / n) * n * 1.0 / (n - i);//要移项
}

还有一种办法是按照分手是祝愿那题分析，不同的是没有“抽错”的代价

P4397 [JLOI2014] 聪明的燕姿

click

我们知道

\[sum = \prod_{j = 1}^k(\sum_{i = 1}^{\alpha_j}(p_j^i) + 1) \]

那么\(p_j^{\alpha_j}\)就是答案的一个因子

暴力枚举质数会炸，那么考虑搜索

每次枚举\(\sum_{i = 1}^{\alpha_j}(p_j^i) + 1\)，能够整除时进入下一区块并用\(p_j^{\alpha_j}\)更新符合条件的数

void dfs(int now,int id,int num)
{
	if(now == 1)//不能解分解
	{
		ans[++res] = num;
		return;
	}
	if(isprime(now - 1) && now > pri[id]) ans[++res] = num * (now - 1);//形如1+p的区块
	for(int i = id;pri[i] * pri[i] <= now;i++)
	{
		//cout << 114 <<endl;
		int base = pri[i];//p_j^(a_i)
		int sum = pri[i] + 1;区块总和
		for(;sum <= now;base *= pri[i],sum += base//更新最高次幂和综合)
		{
			if(now % sum == 0) dfs(now / sum,i + 1,num * base);//进入下一区块并用最高次幂更新答案
		}
	}
}
//记得要给ans数组排序

P4492 [HAOI2018] 苹果树

不好好考概率的题

是的，因为你会发现所有树的出现概率都是\(\frac{1}{N!}\)，那就只需要得到所有树的总距离之和就行了

求这个东西是组合（CaO）

我们不从点入手，从边开始，考虑一条边的贡献

对于\(edge(u,v)\)，当\(以v\)为根，大小是\(siz_v\)（包含\(v\)）的子树内的点向外走时都会经过这个边，那么贡献就是\(\large siz_v(n - siz_v)\)

我们可以枚举\(v,siz_v\)来累计答案

接下来考虑子树内和子树外点的分布（编号和形态）

对于以\(v\)为根的子树来说，形态上有\(siz_v!\)种（和得到概率为\(\frac{1}{N!}\)一样的方法），再结合先有根再有儿子，\(v\)的儿子们的标号肯定\(\in [v+1,n]\)
从中选择的方案有\(C_{n - v}^{siz_v - 1}\)种（除去根），所以内部方案就是\(\large siz_v!C_{n-v}^{siz_v-1}\)

对于子树外部，根节点为\(1\)不变，剩了\(n - siz_v-1\)个点，长出\(1\sim v\)这一部分有\(v!\)种形态，结合这些点都不在\(v\)的子树内，我们发现，\(1 \sim v - 1\)这些点都可以作为连接点并不断延伸下去，方案是\((v - 1)v(v + 1)\cdots (n - siz_v - 1)\)，那么总方案就是\(v!(v - 1)v... = \large v(v - 1)(n - siz_v - 1)!\)

所以

\[ans = \sum_{v = 2}^{n}\sum_{siz_v = 1}^{n - v + 1}siz_v(n - siz_v)siz_v!C_{n-v}^{siz_v-1}v(v - 1)(n - siz_v - 1)! \]

//用递推法求组合数
for(int i = 2;i <= n;i++)
{
	for(int siz = 1;siz <= n - i + 1;siz++) 
	{
		ans = (ll)(ans + siz * (n - siz) % p * jie[siz] % p * C[n - i][siz - 1] % p * i % p * (i - 1) % p * jie[n - siz - 1] % p) % p;
	}
}

P2221 [HAOI2012] 高速公路

又一道披着概率外壳的2B题

对于每次询问，分母就是\(\frac{len(len - 1)}{2}\)，所以只需要维护分子，到时候同除以一个\(gcd\)就完了

所以本质还是维护区间修改和区间和

暴力最高水\(40\)（这是蒟蒻水平，有人能直接水过去）

那就上数据结构呗

不想写线段树

和上道题一样，考虑一条边会被走几次

后面为了方便，边\((i,i + 1)\)存在\(val_i\)里

对于\((i,i + 1)\)，左边有\(i-l+1\)个点（\(l \sim i\)），右边有\(r - i\)个点（\(i + 1\sim r\)）所以一次查询的答案就是

\[\sum_{i = l}^{r-1}val_i \times(i - l + 1)(r - i) \]

拆开

\[(l + r - 1)\sum_{i = l}^{r-1} ival_i + (r - lr)\sum_{i = l}^{r-1} val_i - \sum_{i = l}^{r-1} i^2val_i \]

维护\(ival_i,val_i,i^2val_i\)的区间和就行了

对于修改（举个例子）：

\[\sum i^2(val_i+\Delta val) = \sum i^2val_i + \sum i^2\Delta val \]

加的是后面一部分

又臭又长的代码就不放了

2024.5.2

T1 时间复杂度

click

大模拟，细节题

考场上挂了\(50\)是因为\(O(n^w)\)的\(w\)处理挂了

然后改到\(80\)多就改不动了

这种题没数据就看不出问题

目前最高record

T2 Emiya 家今天的饭

click

卫宫教的

考场上看出和组合有关，没搞出式子，骗了\(n=2\)就滚蛋了

有些性质get到了

• 每行只能选一个框

• 每列选的框数不超过总菜数一半

发现第二个性质不好维护，列与列之间微调一下就成了新方案

但是他的反面却很简单：最多只有一列框数会超过一半

所以考虑容斥

那么可以枚举不合法列，然后总数-总不合法就行了

假设当前枚举第\(c\)列不合法，那么这一列的框数一定比其他所有列的框数加起来还要多

结合行与行之间相对独立，可以使用\(dp\)

设\(dp_{i,j,k}\)表示当前在第\(i\)行，第\(c\)列选了\(j\)个，其他列选了\(k\)个，再设\(sum_i\)为第\(i\)行的总和

因为一行只能选一个，所以这一个要么在\(c\)列上要么在其他列上

在\(c\)列上，选的就是\(a_{i,c}\)，和\(dp_{i - 1,j - 1,k}\)搭配

不在，则除\(c\)列外每一列的框都能和\(dp_{i - 1,j,k - 1}\)搭配

还可以不选，累计上一行状态

所以

\[dp_{i,j,k} = dp_{i-1,j,k} + dp_{i - 1,j - 1,k} \times a_{i,c} + dp_{i - 1,j,k - 1} \times (sum_i - a_{i,c}) \]

第\(c\)列的非法总数就是

\[\sum_{j > k}dp_{n,j,k} \]

总数：每一行可选总数为\(sum_i\)，算上不选是\(sum_i + 1\)，则总数为

\[\prod_{i = 1}^n(sum_i+1) \]

那么合法的就是\(总数 - 非法 - 1\),这里的-1是啥也没干的情况

把m打成n都有60就很难评

record

接下来优化，肯定是压\(dp\)的维数

发现后两维一定满足\(j > k\)，故不妨合成一个\(j - k\)的维度，记为\(l\)

那么

\[dp_{i,l} = dp_{i - 1,l} + dp_{i - 1,l - 1} \times a_{i,c} + dp_{i - 1,l + 1}\times (sum_i - a_{i,c}) \]

其他的不变

考虑到维护差值，就要平移防止下标为负

坑点：初始化也平移了，\(dp_{0,N} = 1\)

record

T3 P7098 [yLOI2020] 凉凉

click

好名字

\(dfs\)应有\(35\)，但我没有

状压铁路修没修状态，但不知道深度和铁路状态咋搞

后来一看，全TM是预处理了

• 第\(i\)条地铁修在\(j\)深度的花费 \(val_{i,j}\)

• 是否相撞的\(vis_{i,j}\)

• 在深度\(i\)修建状态为\(S\)的花费\(w_{i,S}\)

对于\(w\)的更新稍微说一下：枚举\(S\)，把\(S\)中涉及的地铁拎出来，用\(vis\)判状态是否合法，不合法值就是\(inf\)

然后就是超简单\(dp\):

\[dp_{i,S|s} = \min(dp_{i-1,S} + w_{i,s}) ，其中S \& s = 0，因为一条地铁只能修一次 \]

得到一个record

\(T\)的原因是\(dp\)中的大小\(S\)复杂度来到\(2^{2n} = 268 435 456\)，非常吓人

这时有个巧妙方法：我们可以枚举\(S\)的子集和对应补集来更新\(S\)

for(int s = S;s;s = (s - 1) & S)
	dp[i][S] = min(dp[i][S],dp[i - 1][S ^ s] + w[i][s]);

这样就过了

T4 [联合省选 2020 A]树

click

想水链的\(20\%\)，没水到

可以使用\(Trie\)数维护异或和，但也有没用的

用的差分（？？！？！？！？！）

规定：\(u\)第\(i\)级的祖先表示深度相差\(i\)的父节点

我们发现，深度增加（减少时），就是所有的\(d\)增加（减少）\(1\)，即所有异或的数字增加（减少）\(1\)

所以重点就是维护整体变化事的异或和，这样就能从子节点出发计算贡献

由于是位运算，考虑按位计算贡献

类比十进制或是手算可得：改变百位需要加\(10^2\)，那么二进制中改变第\(k(可以为0)\)位就是加\(2^k\)

进一步的，第\(k\)位的变化随着加\(1\)呈现循环，每个循环节中有\(2^k\)个\(0\)，\(2^k\)个\(1\)，长度\(2^{k+1}\)

再把\(+1\)和深度对应

也就是说，异或某点的时候，对于第\(k\)位，该点的

\[[a + 2 ^{k + 1}\times j,(a + 2 ^{k} - 1) + 2^{k+1}\times j],j \in [0,...] \]

级祖先对应的第\(k\)位都是\(1\)（即给祖先异或一个\(2^k\) ），其中\(a\)是循环节中第一个\(1\)的位置，区间形式可类比三角函数单调区间

每次\(+1\)就只对这些区间有影响，修改这些区间可以使用差分

具体的，对上面区间的左端点和右端点\(+1\)分别异或\(2^k\)，取通式就是\(a + 2^k \times j\)

但区间又有一大堆

但再看通式就发现\(a\)是不变的，即\(\operatorname{mod}2^k\)一样，不妨从此处下手

设\(s_{k,a}\)就表示\(\operatorname{mod}2^k=a\)的一系列点，再观察可得这些点的深度都是有规律的

后续操作及代码参照第一篇题解

太吊了我一定写不出来

然后看看一般的\(Trie\)树方法

2024.5.3

发现现在思维痼疾一堆，没救了

T1 Stack of Presents

click

思路想到了

考虑到放回去时可以改变顺序，因此对于每次需要挪动前面礼物的位置\(pos\)，如果送礼序列中连续若干个礼物的位置在\(pos\)前，则能够通过放回时的排列使得这些礼物对时间的贡献均为\(1\)（连续从栈顶取）

本来记录个\(pos\)就行了，但好像习惯性的写了个循环上去。。。

while(t--)
{
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	last = 0;//上一个需要挪动前面礼物的位置
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]),pos[a[i]] = i;
	for(int i = 1;i <= m;i++) scanf("%d",&b[i]);
	ll ans = 0;
	int cnt = 0;//已经送出的礼物数
	for(int i = 1;i <= m;i++)
	{
		if(pos[b[i]] < last) ans++,cnt++;//在挪出位置前，可以通过改顺序使其贡献为1
		else ans += 2 * (pos[b[i]] - cnt - 1) + 1,cnt++,last = pos[b[i]];
	}
	printf("%lld\n",ans);
}

T2 棠梨煎雪

click

在某oj上暴力碾了std可海星

如果有\(k\)列全是问号，答案就是\(2^k\)

而且如果有一列有\(0\)又有\(1\)，肯定没戏

暴力就是枚举每一列和\(l\sim r\)排除没戏的情况，\(O(nmq)\)应有\(45pts\)

优化也是优化这里并将两种操作合并

区间查询可以使用线段树+位运算，大不了就是开30棵

对于问号位，我们只关心这一列有没有已知元素，因此出现问号时，问号赋为\(0\)，已知赋为\(1\)，没问号的列肯定还是要赋成准确值

由于已知出现一个就确定了这一列，所以使用 | 运算

代码可参照这位巨佬的

T3 打砖块

click

\(dp\)

本来按坐标\(dp\)整的，结果状态就不对，处理子弹分配的时候乱的一p，就死了

还把本来是预处理的操作曰到\(dp\)初始化里了

考虑子弹只会竖着走，所以把每一列打包，预处理搞

定义\(sum_{i,j}\)表示第\(i\)列花费\(j\)颗子弹时的得分，\(dp\)定义同理

然后这题的坑就在\(Y\)上

在打包列的时候，会把\(Y\)宏观等价认为是子弹没有损耗白挣分，但这样有失偏颇

• 得有子弹去打\(Y\)

• 从\(Y\)得到的子弹不一定继续沿着这一列打，样例就是

结合第二条，就有必要在\(dp\)和预处理中区分是否在这一列打光子弹，且打\(Y\)时得到的子弹是否继续在这列使用

因此，记\(sumY\)表示从\(Y\)得到的子弹继续在该列使用，此时等价认为生效

再记\(sumn\)表示相反，此时等价认为无效

拿样例来说,\(sumY_{2,1} = 7\)，相当于认为只消耗了一发就打碎下两个块

而\(sumn_{2,1} = 2\) ，\(sumn_{2,2} = 7\)，相当于认为一发就是打了最下面，两发就是打了下两块。至于\(Y\)的奖励，拿去打第一列了，所以打第二列下两块就是用了两发

那么这样一来就能模拟第二条了

相应的把\(dp\)新增一维表示在这列打到了\(Y(1)\)还是\(N(0)\)，或者说是等价认为是否生效

dp[i][j][0] = max(dp[i][j][0],dp[i - 1][j - l][0] + sumY[i][l]);//整合Y 
if(l > 0) dp[i][j][1] = max(dp[i][j][1],dp[i - 1][j - l][0] + sumn[i][l]);//第i列收尾, 奖励给j-l那部分留着，此时前面停到了N 
if(j > l) dp[i][j][1] = max(dp[i][j][1],dp[i - 1][j - l][1] + sumY[i][l]);//第i列收尾，l颗和奖励都梭哈到第i列，那么对于j-l部分来说j-l发也是全梭哈的 

坑点：

1.\(sumn\)的更新用的是\(sumY\)，相当于把连续\(Y\)的权值赋到这一串\(Y\)下面的\(N\)

if(vis[i][c])
	sumY[c][cnt] += a[i][c];//等价认为不消耗
else
{
	++cnt;//新增一发
	sumY[c][cnt] = sumY[c][cnt - 1] + a[i][c];
	sumn[c][cnt] = sumY[c][cnt - 1] + a[i][c];
}

2.答案不比大小，就是\(dp_{m,k,1}\)

T4 斗地主

click

考试的时候先水了\(20\)，然后认识到是搜索，但没时间写了

根据经验来说，肯定先挑一次出牌多的方法出（当然也不一定，所以搜索而非纯贪心）

因此先看顺子，再看带牌

还有一点就是，对牌，三牌，炸弹什么的其实不用特意判断看，因为每种牌最多不超过四张，出法还都是单一数值（没有组合），所以只需最后遍历一遍，还有剩的话再出一次就行了

record

2024.5.19

概率期望组合乱杀赛

T1&T4 P5516 [MtOI2019] 小铃的烦恼

click

矩阵没有意义，因为每个都是\(1.0\)

有点像分手是祝愿，但又很不一样

设\(x_i\)表示某颜色（不妨设为\(A\)）从\(i\)个改成\(n\)个的期望步数

一个操作分两大类三种情况：

• 把一个颜色改成\(A\) ,花了1步，再花\(x_{i+1}\)步即可
• 把\(A\)改成别的，同上，共花了\(1 + x_{i-1}\)步
• 与\(A\)无关

设修改涉及到\(A\)的概率为\(k = \frac{2i(n-i)}{n(n-1)}\)

对于第一大类，差别只在于\((A,B)\)还是\((B,A)\)，所以两种情况各占\(\frac{1}{2}\)，且都涉及了\(A\)，所以系数是\(\frac{k}{2}\)

对于第二大类，没有修改\(A\)，系数\(1 - k\)

考虑到所有的都是操作了一步，所以有式子

\[x_i = \frac{k}{2}(x_{i-1}+1) + \frac{k}{2}(x_{i+1}+1) + (x_i + 1)(1-k) \]

化简得到

\[x_i = \frac{1}{2}x_{i-1} + \frac{1}{2}x_{i+1} + \frac{1}{k} \]

然后根据经验可知这东西退化成\(dp\)

就完了？

没有

事实上，还存在着改着改着\(A\)就没了，所以还得加条件

设\(p_i\)表示能把\(A\)从\(i\)个改成\(n\)个的概率

还是上面的两大类，再把修改\(A\)的概率设为\(k\)，对于第一大类，对应的概率都是\(k\)，对于第二大类，对应的概率就是\(1 - 2k\)，就有

\[p_i = kp_{i+1} + kp_{i - 1}+(1-2k)p_i \]

化简得到

\[p_i = \frac{p_{i+1}+p_{i-1}}{2} \]

这是个等差数列，再结合定义得到

\[p_0 = 0,p_n = 1 \]

可以算出

\[p_i = \frac{i}{n} \]

那么根据条件概率，所有的步数都要乘上对应的可行概率，所以得到

\[p_ix_i = \frac{1}{2}p_{i-1}x_{i-1} + \frac{1}{2}p_{i+1}x_{i+1} + p_i\frac{n(n-1)}{2i(n-i)} \]

再代入概率表达式

\[\frac{i}{n}x_i = \frac{i-1}{2n}x_{i-1} + \frac{i+1}{2n}x_{i+1} + \frac{n-1}{2(n-i)} \]

这样的话，再根据退化成线性，就可以跑一个高斯消元板子的简化版求出\(x\)，然后还要补上条件概率（只存部分系数一把弄下来）

但是有点麻烦，还可以设\(dp = x \times p\)，那么答案就是\(dp\)

那就会有

\[dp_i = \frac{1}{2}dp_{i-1} + \frac{1}{2}dp_{i+1}+\frac{n-1}{2(n-i)} \]

\[dp_0 = dp_n = 1 \]

即

\[dp_i - dp_{i-1} = dp_{i + 1} - dp_i + \frac{n-1}{n-i} \]

相当于每次的差就是给上一次的差加一个数，特殊的是，最初的差（没加数）就是\(dp_1 - dp_0 = dp_1\)，所以可以求出\(dp_1\)

从\(dp_0 \to dp_i\)有\(i\)个差，且每次加上的最后一项还会累加，所以

\[dp_i = dp_0 + idp_1 + \sum_{j = 1}^{i - 1}(i -j+1)\frac{n - 1}{n - j} \]

令\(i = n\)（因为\(dp_n = 0\)）

\[dp_n = ndp_1 - (n-1)(n-1) = 0 \]

得到\(dp_1 = \frac{(n-1)(n-1)}{n}\)

然后就递推了

T3 [JXOI2018] 游戏

click

组合

第一次读错题了，后来才发现是怎么回事

就是\(2,4,3\)这组排列

虽然提醒\(2\)会使得\(4\)会工作，但是\(3\)没有工作，所以为了检查\(3\)，还得走\(4\)再走\(3\)，所以时间是\(3\)

这也就是说：时间就是从头开始，一直到最后一个未被提醒的位置

显然，未被提醒就是前面没有自己的因子，我们可以把这类数预处理出来，假设有\(k\)个

那么问题就变成了一个期望问题：最后一个数的位置（相对于开头）是权值，与落到该位置的概率相乘并求和，再给最后的答案乘以\(n!\)（消去概率，很显然所有概率分母都是这个）

对于一个特殊数，它可能的最后位置应该在\([k,n]\)，假设在\(i\)

那么同时，剩下的\(k-1\)个数一定都在前面\(1 \sim i-1\)中，这样的分布有\(C_{i-1}^{k-1}\)种

总的分布是\(C_{n}^{k}\)，那么分布上的概率就是\(\frac{C_{i-1}^{k-1}}{C_{n}^{k}}\)，权值是\(i\)

所以

\[ans = n! \times \sum_{i = k}^{n}(\frac{C_{i-1}^{k-1}}{C_{n}^{k}}\times i) \]

尝试化简：

\[\begin{aligned}n! \times \frac{C_{i-1}^{k-1}}{C_{n}^{k}}\times i &= n! \times \frac{(i-1)!}{(k-1)!(i - k)!} \times \frac{k!(n-k)!}{n!} \times i \\&= \frac{i!k!(n-k)!}{(k-1)!(i -k)!} \\&= \frac{i!}{(k-1)!(i-k)!} \times k!(n-k)! \\&= \frac{i!}{k!(i-k)!} \times k \times k!(n-k)!\end{aligned} \]

所以

\[ans = k \times k!(n-k)!\times \sum_{i = k}^{n}C_{i}^{k} \]

最后一个西格玛很熟悉了，就用公式\(C_n^m = C_{n-1}^{m-1} + C_{n-1}^{m}\)，补一个不存在的\(C_{k}^{k+1}即可\)，答案就是\(C_{n+1}^{k+1}\)

所以

\[ans = k \times k!(n-k)!\times \frac{(n+1)!}{(k+1)!(n-k)!} = \frac{k}{k+1}(n+1)! \]

ps:代码实现时用埃筛思路即可，但为了速度要把标记数组开成\(bool\)

T2 SSY的队列

click

\(70pts\)的状压，\(std\)的记搜

状压：\(0/1\)表示是否进入队列，设\(dp_{i,S}\)表示最后一个人是\(i\)，状态为\(S\)是的方案数，答案是\(\sum\limits_{i = 1}^{n}dp_{i,2^{n}-1}\)

码子

接下来通过优化状态，我们可以得到如下性质：

• 我们可以按照膜\(m\)的余数将所有数字分类，则不同类的数字相邻一定合法，考虑到同一类的数等价， 那么答案就是对类的排列方案数乘上每个类所含数个数的阶乘，设\(f_{k,a1,a2,...a_n}\)表示当前最后一个数为第\(k\)类，各类数用掉了\(a_1,a_2,...a_n\)个

• \(a_1,...a_n\)顺序无关，即对于\(\forall i,j,\)若\(a_i = a_j\)，则\(f_{i,a_1,a_2,...,a_n} = f_{j,a_1,a_2,...,a_n}\)，这个性质可以用来使得\(a_1\leqslant a_2 \leqslant...a_n\)，减少了状态数

参考代码

2024.6.2

T4 围栏障碍训练场

click

写\(dp\)老想不起来写预处理啊啊啊

状态都想好了，\(dp_{i,0/1}\)表示走到\(i\)号篱笆的左端/右端的最小步数

然后每次更新都要用上一次的左端点和右端点来更新

这个“上一次”就是预处理的内容（不好处理也可以类似的处理“下一次”）

然后没写，硬存每次新的左右端点，拉了一大坨才\(40\)

考虑到预处理是\(n^2\)的，难说过不过

预处理“下一次”，dp意义稍有不同

啊，\(T\)了

再优化的话，可以使用区间覆盖+单点查询，即每个区间把自身范围内的高覆盖成自己所在高度，然后对于端点，每次查询一下就可以了

要写线段树，like this

T1 等差子序列

click

想着是用差分数组乱搞暴力，但是还有更简单的

枚举差值得数值，再判断一下位置单调性和数值单调性是否同步就可以\(n^2\)水过去

注意的是单调性有增有减

record

T2 [Jsoi2015]非诚勿扰

click

我们先计算一下对于第\(i\)个女人，她的列表内第\(j\)个男人被选中的概率

以第一个人为例，他被选中的概率 = 直接被选中的概率 \(+\) 列表循环一次后被选中的概率 \(+\) 列表循环两次后被选中的概率 \(+\) \(...\)

设列表长度为\(len_i\)，那么每次的概率就是前面的人都选不上乘以自己被选上，即

\[P = (1-p)^0p + (1-p)^{len_i}p + (1-p)^{2len_i}p + ... = \sum_{i = 0}^{\inf}(1-p)^{ilen_i}p \]

然后

\[P - (1-p)^{len_i}P = p \]

\[P = \frac{p}{1 - (1-p)^{len_i}} \]

类似的，就能得到第\(j\)个男人被选中的概率为

\[P_{i,j} = \frac{(1-p)^{j-1}\times p}{1 - (1-p)^{len_i}} \]

对于一对女人\((p,q)\)，如果一对男人\((j_1,j_2)\)符合条件，那么贡献就是\(P_{p,j_1}\times P_{q,j_2}\)，所以该对女人的贡献就是所有符合条件的\((j_1,j_2)\)的概率乘积和

观察要求形式，可以使用树状数组实现类似求逆序对的方法维护

like this

T3 [CSP-S 2021] 括号序列

click

考虑使用题目给的规则扩展，所以是区间\(dp\)

定义\(dp_{i,j,id}\)表示\([i,j]\)字符状态为\(id\)的方案数，其中对\(id\)有如下规定

• \(id = 1\)：形如 (...) 的字符串

• \(id = 2\)：形如 ***..** 的字符串

• \(id = 3\)：形如 (...)**..*(...)的字符串，即左右均为括号

• \(id = 4\)：形如 (...)*...*(...)**的字符串，即左边为括号，右边为 *

• \(id = 5\)：形如*..*(..)的字符串，即左边为*，右边为\(()\)

• \(id = 6\)：形如 *..*(..)***的字符串，即左右均为 *

接下来搞\(dp\)

• \(dp_{i,j,1} = dp_{i + 1,j-1,2} + dp_{i+1,j-1,4}+dp_{i+1,j-1,5}+dp_{i+1,j-1,3}\)，前提是\(i,j\)能配成一对括号

  • 含义是括号内除了两边是星星的情况不合法其他均可

• \(dp_{i,j,2}\)特判即可

• \(dp_{i,j,3}= \sum\limits_{k = i}^{j-1}(dp_{i,k,3}+dp_{i,k,4})\times dp_{k+1,j,1} + dp_{i,j,1}\)

  • 含义是第3,4种满足左边为括号开头，然后右边补一个括号，是情况1，还有一种特殊的是整个是一个括号序列

• \(dp_{i,j,4}=\sum\limits_{k=i}^{j-1}dp_{i,k,3}\times dp_{k+1,j,2}\)

  • 含义是在第3种情况后面加一串星星构成第四种情况

• \(dp_{i,j,5} = \sum\limits_{k=i}^{j-1}(dp_{i,k,5}+dp_{i,k,6})\times dp_{k+1,j,1}\)

  • 含义是开头为星星的为第5,6种情况，在结尾补一个星星成为情况5

• \(dp_{i,j,6} = \sum\limits_{k=i}^{j-1}dp_{i,k,5}\times dp_{k+1,j,2} + dp_{i,j,2}\)

  • 含义是在开头为星，结尾为括号的情况后面补一串星得到第六种情况，特别的，全是星属于该情况

答案为\(dp_{1,n,3}\)

code

2024.6.9

T1 小奇挖矿2

click

还没悟透，还得悟

\(O(m)\)裸\(dp\)有\(60\)

这道题有一个很○○的性质：如果两个行星之间的距离\(\geqslant 18\)，那么这从一个星球一定可达另一个星球

得到这个性质可以打表，也可以用一些奇奇怪怪的数学定理（因为此时距离可以写成\(4a+7b\)的形式，应当和不定方程有关）

这样，我们就可以离散化，把位置从星球编号变成距离，如果两星球间距离大于十八，就只给距离加18就行了

注：

• 方便起见可用倒序

• 别老惦记着map,会被卡到\(70\)

code

T2 小奇的矩阵(matrix)

click

式子都有了

设\(n + m - 1 = k,sum = \sum\limits_{i = 1}^{n + m - 1}A_i\),则

\[\begin{aligned}原式 &= \frac{1}{k}\sum(kA_i-sum)^2 \\&= \frac{1}{k}\sum((kA_i)^2 - 2kA_i \times sum + sum^2) \\&= sum^2 + \sum(kA_i^2 - 2A_i\times sum) \\&= sum^2 + k\sum A_i^2 + 2\times sum\sum A_i \\&= k\sum A_i^2 - sum^2\end{aligned} \]

接下来就要维护平方的和以及和的平方

然后就到了本蒟蒻必翻车环节：可以把和扔进状态枚举，反正最大才\((30 + 30 - 1) * 30 < 1800\)

所以定义\(dp_{i,j,S}\)表示走到了\((i,j)\)，元素和为\(S\)时的平方和

那么当\(S \geqslant a_{i,j}\)时就从左边和上边转移即可

初始化：\(dp_{1,1,a_{1,1}} = a_{1,1}^2\)

code

后面两道都和树有关，难绷

T3 小奇的仓库(warehouse)

click

先不管异或，用树剖求有\(30\)

稍微解释一下solve:对于父子节点\(u,v\)和边\((u,v)\)，\(v\)到自己子树内不走这条边，\(-siz_v\)，到u其他子树和u外面部分都要走这条边，\(+(n - siz_u)+(siz_u - siz_v)\)

然后看看异或

观察到\(M \leqslant 15\)，也就是说异或顶多影响后四位，所以可以暴力单独维护

T4 Kamp

click

树型dp里的题但我跳了

树形\(dp\)通常都分树内和树外两种情况。所以往往变量成对

对于此题，我们可以定义\(f_u\)表示把\(u\)子树内的人送完的花费，\(g_u\)表示把\(u\)外面的人送完的花费

那么对于边\((u,v)\)，如果\(v\)内有人，那么就要进入\(v\)的子树送完人后再出来。所以\(f_u = f_v + 2 \times W_{(u,v)}\)

类似可得\(g\)的计算方法：

\[g_v = g_u + (f_u - f_v) \]

特别的，根没有\(g\)

那么，对于以点\(x\)为起点（根）的情况，答案自然就是\(f_x + g_x\)····吗？

我们回到\(f_u\)的计算方式，可以发现每条边都算了两次，也就是说 \(f_u\)表示的是送完\(u\)内的人并且回到\(u\)点的花费

那\(g\)也一样

但实际上，送完最后一个人后没必要回来，所以有两种选择

• 先\(u\)外再\(u\)内，停在\(u\)内不回来

• 先\(u\)内再\(u\)外，停在外面不回来

每种方案都是在原来和的基础上减掉一个回来的花费

那么减掉的肯定越大越好，所以就是求以\(u\)为起点的最长链，内外两条，取大的减掉

最后有一个细节：计算\(g\)的时候，没有算上\((u,v)\)这条边，但也不能直接加一个二倍，如果\(v\)内有人，就不加了，因为\(f_u\)把这条边算过两遍了

更多见注释

2024.7.6

T1 公式求值

根据样例写出来发现每一位都是个前缀和，搞一搞就行了

code

T2 最长的Y

\(60pts\):枚举每个连续的\(Y\)，左右寻找\(Y\)看能不能合并，指针法

code

std:

考虑初中学过的\(min(|x - a| + |x - b| + ...)\)这类问题就能得到：最终的一段\(Y\)必然是往中间位置汇聚得到的，因为这样最优

然后二分区间按上面类似的方法搞就完了

有一点就是\(O(1)\)得到距离的预处理：

设第\(i\)个\(Y\)下标为\(p\)，那么\([1,p]\)内点点的个数就是\(p - i\)，那么要挪到第\(j\)个下标为\(q\)的\(Y\)旁边，代价就是两个\(Y\)中间的点点数，即\(|(p - i) - (q - j)|\)

可以通过维护前缀和等方法得到距离

code(含注释)

T3 交换序列

把\(T\)成\(0\)蛋的\(dfs\)改写成\(bfs\)有\(30\) ???

接下来考虑另一种方法：不妨枚举加入的字母来合成答案串，再判断一下符不符合条件就行了

合成的串可以使用类似状压的方法压缩表示，有\(60\)

code

想到这里就基本快到正解了

这里有一个隐藏限制：\(k \leqslant len(len - 1) / 2\)

理由很简单，超过这一个之后就可以对序列全排列了，多出来的交换次数没什么用

那么就可以把它扔进\(dp\)里

定义\(dp_{i,j,k,l}\)表示用了\(i\)个\(K\),\(j\)个\(E\),\(k\)个\(Y\)，交换了\(l\)次的方案数

预处理原串中三个字母的数量、位置等，通过枚举新加入的字母来转移答案

code

T4 最长路径

由于数据规模小，所以不妨直接枚举第\(k\)大的数\(tmp\)，\(nm\)的

定义\(dp_{i,j,l}\)为走到\((i,j)\)，经过了\(l\)个\(\geqslant tmp\)的数，如果\(a_{i,j}\)严格大于\(tmp\)，必选，如果严格小于，必不选，等于的话就是可选可不选

但是样例二说明有些相等的情况必须取

那就不妨都先取上，然后再跑一边不取的情况看看能不能更优就行了

五次方的复杂度能过就是了

code

2024.7.8

5道题的一天

T1 分糖果

按余数分，有\(000,111,222,012\)四种

那么就有两大种方案

• 尽可能多的凑\(012\)，剩下的凑\(000,111,222\)

• 尽可能多的凑\(000,111,222\)，剩下的凑\(012\)

两种分别算求\(max\)即可

把j+2写成j + 没删调试痛失100

code

T2 乒乓球

\(30pts\):暴力\(O(n)\)

整洁：

考虑周期 （废话）

大周期就是两个人的比分再次相同的中间经过的部分

但是要注意的是：不是一开始就进入周期

这里用到一个技巧：当\(k\)个球结束时，如果两人分数都超过\(11\)还没分胜负，那么就可以在维持分差不变的情况下缩小比分在\(11\)以内

那么比分最多$12 \times 12 \(中，枚举这么多个\)k$就肯定能找到周期

找到周期后，由于每个周期满足两人赢的局数增量一样，且比分不变，所以可以跳过不少

再把首位未进入周期的部分暴力掉就行了

code

T3 与或

开的ll但scanf %d 痛失暴力分30

这里有一个策略：把|放&后边，值一定不变小

好像也很好理解，\(x\&y|z\)最小是\(z\)，\(x | y\& z\)最大是\(z\)

所以直接把所有|放到最后得到最大值

然后枚举前面，看能不能在不改变值的情况下放|,形成|||..&&&..|..|的样子

这里，为了快速得到||||或者&&&&&的答案，要预处理一个位前缀和，再根据特性搞

code

T4 跳舞

有暴力，但感觉不好打，有用到状压

看数据范围像是区间\(dp\)，但最后竟然只是个预处理？！

设\(ok_{i,j}\)表示能否把\([i,j]\)内的人都消掉，为了实现这个，可以通过找\(i - 1,j+1\)号人跳舞实现

\[ok_{i,j} = or_{k = i}^{j} (ok_{i,k - 1 } \& ok_{k+1,j} \& ([\gcd(a_{i-1},a_k) > 1] | [\gcd(a_{k+1},a_{j+1}) > 1])) \]

然后定义\(dp_{i}\)表示对于前\(i\)个人，留下第\(i\)个人，最多能消掉多少人，那么

\(dp_{i} = \max\limits_{j=1}^{i} ((dp_j + i - j - 1) \times ok_{i+1,j-1})\)

这里要\(dp\)到\(n+1\)，因为第\(n\)个人也不一定留着

code

T5 音乐播放器

很熟悉了

肯定要做\(01\)背包

如果第\(i\)首歌结尾，那么它就不能在前面出现，所以要用剩下的音乐填满\([S-a_i,S)\)这一部分

接下来根据样例，我们需要计算如果前面出现了\(j\)首不同的歌曲（算上最后一首一共\(j+1\)首不同的），对应概率是多少（补充：放了\(x\)首，剩下的新歌概率都是\(\frac{1}{n-x}\)）

这里可以借鉴非诚勿扰的等比数列方法：

\[\begin{aligned}P(j+1) &= \frac{1}{n} \times \prod\limits_{k = 1}^{j}\frac{k}{n} \times (1 + \frac{j + 1 - k}{n }+ (\frac{j+1-k}{n})^2 + ...) \\&= \frac{j}{n}\times \frac{n}{n-1} \times \frac{j-1}{n}\times \frac{n}{n-2}\times ...\times \frac{1}{n} \times \frac{n}{n-k}\times \frac{1}{n} \\&= \frac{k!(n-k-1)!}{n!}\end{aligned} \]

此处介绍另一种方法:

..

2024.7.9

T1 超市抢购

只要当前不够就从后一个搬，哪怕后一个也不够，反正后面会补齐的

ll ans = 0;
for(int i = 1;i <= n;i++)
{
	if(delt[i] < 0)
	{
		ans += abs(delt[i]);
		delt[i + 1] -= abs(delt[i]);
	}
}
cout << ans; 

T2 核酸检测

dp

定义\(dp_i\)表示在第\(i\)时刻喊了一声，并且让所有\(l \leqslant i\)的人下来做核酸的最少方法数量

转移就是\(dp_{j} = \min_{i<j}(dp_i + 1)\)

接下来考虑\(j\)的条件

根据\(dp\)定义，新加的\(1\)肯定是在\(j\)时刻喊的，那么\([i + 1,j - 1]\)中间就没喊，所以要保证没有区间完整的处于其中

那么就要保证开头在这个区间内的区间的右端点都大于\(j\)

可以预处理一个\(R_i\)表示以\(i\)为开头的区间中右端点的最小值，那么\(j \leqslant \min\limits_{k = i + 1}^{j - 1}R_k\)。写在码里就是更新循环上界

由于要覆盖最后一个区间，所以在\(l,r\)的最大值中找答案

接下来考虑求方案

如果\(dp_i\)给\(j\)有贡献，就累计\(i\)处的方案，否则继承

code

T4 龙珠游戏

屌题

数据明示区间\(dp\)，但是神龙的取法会使得区间不稳定（它随便取），要转化

明确的一点是，如果神龙拿走的珠子不在端上，其实可以选择“不取”，反正小明取不到

那么怎么弥补没取的次数呢？

我们可以让神龙在某个时刻从左（右）端连续取走若干个珠子

这样就把两人的操作都限制在端点处，可以搞一搞\(dp\)了

定义\(xm_{i,j,k},lo_{i,j,k}\)分别表示小明/龙在决策区间为\([i,j]\)，龙能连续取\(k\)次的最大/最小总和（神龙希望小明得分少，所以对应最小）

那么分类

小明：必须取左/右端，此时龙决策完了

龙：

• 取左/右端，消耗一定次数

• 放弃，继承小明的状态

就有方程

\[xm_{i,j,k} = max(lo_{i + 1,j,k + 1} + a_i,lo_{i,j - 1,k + 1} + a_j) \]

\[lo_{i,j,k} = min(xm_{i,j,k},lo_{i + 1,j,k - 1},lo_{i,j - 1,k - 1}) \]

答案：\(xm_{1,n,0}\)

code

T3 七龙珠

竟然用背包我服了呀（想到了不敢写）

后面写对的话瓶颈就是背包的\(O(\sum x_iM)\)

突破以后再说，要用科技，不用上限\(80\)

那么背包出来可以拼出的合法龙珠后从大到小排序（系数为负的话从小到大，注意记得算上能量值为\(0\)的龙珠）

有两种写法

• \(bfs\)

最大的肯定是每组最大值，记为\((1,1,1,1,1,1,1)\)，那么次大的就是\((2,1,1,1,1,1,1),(1,2,1,1,1,1,1)...\)，再往后就是\((1,2,2,1,..)..\)，妥妥的\(bfs\)，每次给单个组的排名加一，把值扔进优先队列搞

重点是去重，想办法搞搞，比如\(hash\)什么的

code

• dfs

目前有个剪枝就是排名\(\geqslant \prod a_i\)，\(a_i\)就是上面括号里的东西，这个东西比\(k\)大肯定没戏

能拿\(50\)

2024.7.10

\(O(n)\)能过\(1e8!\)

\(O(n)\)能过\(1e8!\)

\(O(n)\)能过\(1e8!\)

T1 算术求值

模拟出\(kx+b\)枚举\(x\)就行了

......

T2 括号序列

先把能配上的扔掉，然后相邻两个一组按下列方式计算代价

• \("(("\) 或 \("))"\)：代价为\(1\)

• \(")("\)：代价为\(2\)

完了

code

T3 Count Multiset

dp

可以做背包搞，有\(40\)

ll dp[N][N][N];//dp[i][j][k]: 考虑前i个数,有j个不为0，和为k 
int n,m;
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin >> n >> m;
	dp[0][0][0] = 1;
	for(int i = 1;i <= n;i++)
		for(int j = 0;j <= n;j++)
			for(int k = j;k <= min(i * j,n);k++)
				for(int o = 0;o <= min(m,j) && o * i <= k;o++) //枚举重复元素数量，重复的就是i 
					dp[i][j][k] += dp[i - 1][j - o][k - o * i];
	for(int i = 1;i <= n;i++) cout << dp[n][i][n] << endl;
	return 0;
}

补上取余能到70

std:

继续沿用补\(0\)的思想，定义\(f_{i,j}\)表示考虑了前\(i\)个数，和为\(j\)，那么有两种转移

• 补一个\(0\)，从\(f_{i-1,j}\)转移

• 整体加\(1\)，从\(f_{i,j-i}\)转移

这里巧妙的是通过补\(0\)和整体加构造重复元素，避免了枚举

那么考虑限制条件，很显然第一种操作最多补\(m\)个\(0\)，那么贡献就是\(\large\sum\limits_{k = 1}^{m}f_{i - k,j}\)，但这样相当于规定了序列里一共只有\(k\)个\(0\)，则要求前\(i-k\)个数中不能有\(0\)，这在\(f\)的定义中是看不出来的

所以补充一个\(g_{i,j}\)表示序列里没有\(0\)的情况数，这个的转移就是整体加一的情况，所以就有

\[f_{i,j} = f_{i,j - i} + \sum_{k = 1}^{m}g_{i-k,j} \]

\[g_{i,j} = f_{i,j - i} \]

西格玛可用前缀和优化

code

T4 选数

dfs

分别把质因子给\(x,y\)去搜，然后要枚举幂次

为了防止重复有一些特判

朴素版本\(35\),加上大样例有\(40\)

剪枝：考虑到要保证个数最优，肯定大质数的幂次都是\(1\)，那么不妨把当前\((x,y)\)不断和后面质数相乘且只乘一次直到上限，如果这样都达不到目前的最优解，就不用搜了

\(95\)+大样例 = \(100 (bushi)\)

T5 划分序列

之前有一道类似的

二分最大值，那么两种情况的最大值都不超过二分的值

接下来定义\(dp\)

考虑到有两种代价计算方式，如果分别\(dp\)，可能不从同一处转移

这里巧妙的是，把一种方式作为转移条件

于是，把区间和作为限制

定义\(dp_i\)表示取了\(i\)，并且满足区间和小于二分值的最小代价（单点和）

那么\(dp_i = \min\limits_{j < i,sum_{i - 1} - sum_j < x}(dp_j) + a_i\)

前面的单调队列压线性

code

2024.7.11

上强度了

T1 最短路

数据范围明示\(Floyd\)，但是多了点权

考虑到\(Floyd\)中有枚举中转点的操作，不妨用这个 瞎 搞

将数组排序，就可以保证 \(i \to k\),\(k \to j\)这两条路径的最值点只可能在\(i,j,k\)中，注意这里的\(i,j,k\)不是点，而是排完序后数组的下标

还有一点就是点权不能混进\(dis\)数组搞，要新开一个数组

code

T2 方格取数

为什么有人(Byj大神)四重for有90啊卧槽

各种卡时如枚举长宽，其范围从[1,n]调到[2,n-1]，定义kk为2倍并使用位运算，各种特判+return 0可以获得最少40,最多75

还有clock的，魔法常数的...

教练给的是二分套二分枚举长宽，应该是\(n^2\log^2n\)的

但其实这也是个半玄学，因为对于同一大小的矩形，不同位置的非法情况也不一定相同，和要么小于\(k\)，要么大于\(2k\)，左右界和\(mid\)不好定

还有单调栈+悬线法做的

悬线法就是在某些格子不能选的情况下，处理出每一列的“悬线”，就是最高/低能到哪里，因此每根线都有一个初始位置和高度，接下来就用这根线左右扩展，看能扫出多大的矩形，由于肯定以低的线为界，要用单调栈维护

那么这道题就是先找到一个和\(\geqslant 2k\)的矩形，然后检查每一行，如果一整行的和\(\geqslant 2k\)就要一格一格删，删完把这一行作为答案即可，否则直接删一整行，直到找到一个极大子矩形符合条件

是\(n^2\)的

code

T3 数组

大数据结构题

根据计算公式

\[\varphi(n) = n \times \prod p_i^{\alpha i} \]

可以去分别维护前面的区间乘积和后面的质因数种类

看到\(a_i,x\)都不超过\(300\)，所以对他们都进行质因数分解也顶多用到\(62\)个，那么就可以用一个\(ll\)状压存储有没有第\(i\)个质数

然后就是线段树\(time\)

常数有点大

T4 树

核心就是一个\(\sqrt n\)的暴跳（专业的叫根号分治）

在树上跳\(k\)次可以使用长链剖分的\(k\)级祖先，长链剖分就是把子树深度最大的点当重儿子

板子

预处理\(sum_{i,j}\)表示从\(i\)开始每\(j\)级祖先选一个点，一直选到根节点 的总和

那么就设置一个阈值为\(\sqrt n\)，如果\(c_i \leqslant \sqrt n\)，就用\(sum\)搞一个类似前缀和的东西，把公共的选的部分减掉，但由于左右点到\(lca\)可能不一样，所以重合部分要分开算分别减去

否则暴跳就完了，反正不超过\(\sqrt n\)

要注意的是\(lca\)可能算两遍，要特判

code

2024.7.13

T1 炒币

贪心，找单调区间，峰点买入低谷卖出，都是在区间交界处

code

dp也能搞，但太菜了

T2 凑数

先按性价比（\(x,\frac{y}{a},\frac{z}{b}\)）排序，算先枚举值小的

假设优先级是\(A,B,1\)，那么\(A\)最多用\(\frac{n}{A}\)次，\(B\)最多用\(A\)次（否则可以将一部分\(B\)换成\(A\)，更优），那么\(A,\frac{n}{A}\)一定有一个小于\(\sqrt n\)，那么挑小的枚举即可

注意可以选\(0\)个

code

O(n)dp应有30但RE了就。。。

T3 同构

猜结论或打表

比较好猜的是

• 所含质因子种类相同的数字可以互相换

也好解释，互不互质就看的是质因子

但下面这个就不好猜了

• 所有满足\(\lfloor \frac{n}{x} \rfloor\)相同的质数\(x\)可以互相换

粗略的理解就是有些质数可以和\(1,2,...,\lfloor \frac{n}{x}\rfloor\)相乘从而形成一条链，比如\(n = 14\)时的\(5,10\)

那么如果能交换，很明显链的大小要一样，那么就是\(\lfloor \frac{n}{x}\rfloor\)相同

还有一个就是

• \(1\)和\(> \frac{n}{2}\)的数可以互换

用上面建图方式理解（不互质的连一条边），那么这些数肯定都是单点，互换肯定可以

code

T4 最近公共祖先

考虑黑点的贡献

一个黑点肯定会对自己的子树提供一个备选

再根据询问可知：黑点的祖先 会为 其子树中不含黑点部分 的点 提供一个备选（以该黑点为跳板即可）

那么每更新一个黑点，就可以不断跳父亲来更新对应部分的点的权值

可以\(dfs\)序+线段树维护

但是树的深度未知，跳父亲直到根节点就可能会很慢

事实上，每个点作为父亲产生贡献只需要一次，因为权值是固定的，所以跳到一个已经用过的父亲，就可以停了

但是注意的是，应当先更新完再停，因为即使父亲相同，黑点不同，要更新的子树也不同

code

2024.7.14

爆的最爽的一集

T1 道路

假设原图中两点距离为 \(dis\)，那么操作会：

• \(dis\)为偶数：\(dis' = \frac{dis}{2}\)

• \(dis\)为奇数：\(dis' = \frac{dis+1}{2}\)

可得当距离为奇数时，会多一个1

那么就统计有多少对点的距离为奇数，然后加到原图中任两点距离上，最后除以二即可

那么怎么求距离为奇数点对数呢？

观察\(dis\)的计算：

\[dis = dep_u + dep_v - 2 \times dep_{lca} \]

减数是个偶数，那么加数一奇一偶即可

就是深度为奇数点$\times $深度为偶数点

完了

附：原图中任两点距离计算（考虑边的贡献）：

\[oridis = \sum_{u\in tree}siz_u(n - siz_u) \]

code

T2 集合

最大化异或和的经典做法是\(01 trie\)，然后考虑满足前两个条件

对于条件\(1\)，可以记录树上每个节点中经过该节点的最小值，只要满足\(\leqslant s - x\)就表明存在可行解

对于条件\(2\)，可以得到\(k | v\)，那么就把\(v\)插到\(k\)代表的字典树中作为备选答案（路径），到时候在\(k\)的树上走的时候走到他就是他

又因为不知道\(k\)，所以预处理每个数的所有因数（不只是质因数），到时候就把新加的\(x\)插进其因子代表的字典树中

这里注意进入一个节点的条件：

• 经过该点的最小值\(\leqslant s - x\)

• 该点有编号（存在）

走到中间不行了立刻输出-1

code

T3 科目五

没开\(ll\)爆了\(70\)

二分应该是伪的，但考场上（下）有人能过

问了一下发现\(check\)里二分一次加满油后最远能到的城市可以卡过去（但能优化多少取决于起终点距离，距离小的话几乎没啥用）

后来发现二分能过，但是要随机化加一个\(log\)，那就不会了

code

正解\(dp\)

定义\(dp_{i,j,k}\)表示从城市\(i\)走到城市\(j\)，加\(k\)次油的最大油桶，这里先不考虑\(c_i\)，我们总不能对每次行程都\(dp\)，也没必要

那么方程就是

\[dp_{i,j,k} = \begin{cases} a_j - a_i & k = 0\\ \min\limits_{c = i + 1}^{j}\max(dp_{i,c,k - 1},a_j - a_c) & k > 0\end{cases} \]

朴素版本是\(O(n^4)\)的

接下来用一些奇技淫巧可以发现每次的转移点\(c\)是单调的

那就可以仿照单调队列维护转移点即可 这叫单调指针罢

\(tip:\) 硬开三维\(400 \times 400 \times 400\)会爆空间，可以离散化或者滚动\(k\)

code

T4 监狱

屌题

如果有两个人的路径重叠了，那么这两个人的移动就要有先后顺序

具体的：

• \(A\)的起点在\(B\)的路径上，那么\(A\)应当先于\(B\)走

• \(A\)的终点在\(B\)的路径上，那么\(B\)应当先于\(A\)走

不妨把\(A\)先于\(B\)当作\(A\)向\(B\)连边，那么原问题就等价于连的新图中有没有环

然而重叠部分可能不止一个点，那么某点要连边，就要向路径上所有点连边

如果暴力连接，是平方级别的，但是有分

参考

正解是线段树优化建图... 炸弹还是要炸死人了

2024.7.15

T1 传送带

对于当前所在点\(x\):

设\(l_j\)表示\(x\)左边第\(j\)会让球转向的位置，\(r_j\)同理

那么一共有四种情况：

• 开始向左（右），从左（右）出

这里以开始向左，从左端出为例:

\[\begin{aligned}dis &= x - l_1 + (r_1 - l_1) + (r_1 - l_2) + (r_2 - l_2) + ... + (r_v - l_v) \\&= 2 \times (\sum_{k = 1}^{v}r_k - \sum_{k = 1}^{v}l_k) + x\end{aligned} \]

其他情况照着推即可，比如右始左出时\(x\)要减去，从右出时最后一项应当是\(n + 1 - l_v\)

接下来考虑\(v\)怎么得到

根据样例可得：如果序列中有\(le\)个\(<\)，那么\([1,le]\)从左出，剩下的点从右出

code

T2 math

点击这个再点击目录里的裴蜀定理发现推广2和题目中的形式几乎一样，没取膜而已

那么根据取模尿性，可以猜测

\[\gcd(a_i \operatorname{mod}k) | x \]

但试验后不对

根据取余原始含义可以写出：

\[pk + x = \sum a_ib_i \]

其中\(p\)是整数

然后变一下

\[x = \sum a_ib_i +(-p)k \]

再用一遍裴蜀定理可得到

\[\gcd(k,\sum a_ib_i)|x \]

再根据推广:

\[\gcd(a_i)|\sum a_ib_i \]

所以

\[\gcd(k,a_i) | x \]

那么答案就是\([0,k - 1]\)内\(\gcd\)的倍数

code

T3 biology

设\(f_{i,j}\)表示走到\((i,j)\)的答案，那么

\[f_{i,j} = \max(f_{i',j'} + |i - i'|+|j - j'|) + b_{i,j} \]

肯定爆

然后考虑到\(a_{i,j}\)要单增，再结合题目就没说路径必须是格子挨格子，所以直接开结构体对所有\(a_{i,j} \neq 0\)的格子按\(a\)排序

那么对于\(a_{i,j}\)相同的，就是选一个，最终组成一条路径

那么我们可以对每一条\(a\)相同的“线段”做一个\(dp\)，那么只可能从上一条线段转移而来

对于一条线段，结合原始\(dp\)，拆掉绝对值，可以分成四部分

• \(dp + i -j,dp+ i + j,dp- i + j,dp - i - j\)

开四个变量维护即可

注意的是，在更新\(dp\)时，四个变量必须和当前点\(i,j\)的四种组合一一对应

ll p = h[1] - c[i].x - c[i].y;
ll q = h[2] - c[i].x + c[i].y;
ll r = h[3] + c[i].x - c[i].y;
ll s = h[4] + c[i].x + c[i].y;

code

T4 english

不会

2024.7.24

从此开始难度随机排列

T4 Black and Black

构造

先令\(b_i = i\)，然后计算\(S = \sum a_ib_i\)，如果刚好\(S = 0\)就完了，否则调整

此时已经满足了单调性，为了维护这个东西，最稳妥的方法就是在\(1 \sim i\) 整体减去一个数，或者在\(j \sim n\)整体加一个数

如果\(S > 0\)，说明要减去一个\(S\)，那就是按照上述做法在开头或结尾一部分操作，要在开头减去，需满足\(a_i\)的某个前缀和是\(1\)，这样整体减一个\(S\)即可。要在结尾加，类似的需满足后缀为\(-1\)

\(S < 0\)同理

code

T3 White and Black

如果一个节点是黑的，那么就要统计儿子中是白色的个数，因为这些儿子要变回白色还各需一次操作

那么转化一下就可以变成：儿子数 - 儿子中黑色的个数，因为黑色的儿子肯定在给出的集合中，方便操作

再变一下就是：如果该黑点的父亲是黑色，就省了一次操作

code

T2 White and White

\(dp\)

最裸的就是定义\(dp_{i,j}\)表示把前\(i\)个数分成\(j\)段的最小和，则\(dp_{i,j} = min(dp_{k,j - 1} + (sum_i - sum_k) \% p)\)

然后考虑优化

根据取模性质可以得到：\(dp_{i,...} \equiv sum_i \pmod p\)

对于\(dp_{i,j}\)的两个转移点\(x,y\),有\(dp_{x,j - 1} + (sum_i - sum_x) \% p \equiv sum_x + (sum_i - sum_x) \%p \equiv sum_i \pmod p\)，\(y\)同理

所以\(dp_{x,j - 1} + sum_{x \sim i} \% p \equiv dp_{y,j - 1} + sum_{y \sim i} \% p \pmod p\)

又因为\(sum_{x \sim i} \% p,sum_{y \sim i} \% p\)都小于\(p\)，所以\(dp\)越小，和越小

所以对于每个\(i,j\)，记录转移位置\(pos_{i,j}\)，对于每个\(j\)，用\(i\)更新转移位置

为了压缩空间\(pos\)可以滚动

code

T1 Black and White

四个正解一个不会

\(60\)分做法：预处理出两点距离，最大两点距离和对应的两点，如果修改不影响记录的两点，不管，如果把一个改白了，就在剩的点中重新找最大距离。如果是把一个点改黑了，就把他和原先的黑点配对找最大距离并加入黑点集

code

非魔法能看懂的正解：

维护括号序列，原理等见这里

code

2024.7.25

T1 Permutations & Primes

_yy构造题

\(MEX\)就是区间内没出现的最小数字

首先，要防止\(1\)搅局，所以放到中间，这样包含\(1\)的区间最多

再把较小的质数往两边放，这样能让不含小质数的区间尽量多

再把剩下的合数扔进去，无所谓顺序

code

T2 树上游戏

\(k = n - 1\)时答案就是\(1\)，链的情况下就是均分

正解二分不难想到，重点是\(check\)

首先一般情况下\(check\)都用贪心，就是走了\(mid\)步就放一个，问题就在怎么走

考试的时候口胡了从根走的\(check\)，萎了

正解是每次从最深的点开始，走\(mid\)步后放一个，然后删掉被这个点覆盖的叶子节点，重复这个过程。正确性还算好理解

不太会删点，所以换个方法，本质类似：

设\(f_i\)表示放的点中到\(i\)的最小距离，\(g_i\)表示从\(i\)开始最远能走多远（就是\(i\)到最深点）

那么放点就相当于\(g_i = mid\)，删点就相当于\(f_i + g_i \leqslant mid\)，就是存在一个放好的点能一口气盖到最深点

最后要特判根节点

code

T3 Ball Collector

软肋题（并查集）

考虑给每个路径上点的\(a,b\)连边，那么就变成了从若干连通块中取完所有边，每个边配一个点，求最多能取多少点

画一下图就发现除了树只能拿出\(n-1\)个点外，其它类型（边数\(\geqslant 点数\)）的连通块都可以取出所有点

又因为\(n-1\)恰好是树的边数，所以每个块的贡献还可以写成\(\min(V,E)\)，\(V,E\)对应点数，边数

所以可以使用并查集维护连通块，又因为终点一堆，所以要在回溯时删掉离开的点，就是可撤销并查集

更多细节见码

T4 P7028 [NWRRC2017] Joker

屌题

定义\(p_i,q_i\)为前\(i\)个正数/负数的和，那么（下列所有式子未经说明字母均代表绝对值）

\[s_i = \frac{p_i}{P} - \frac{q_i}{Q} \]

然后就有了两种做法（但本质类似）

• 1.

如果\(i < j\)并且要\(s_i < s_j\)，将上述化简式子带入按照有点熟悉的形式可得

\[\frac{q_i - q_j}{p_i - p_j} > \frac{Q}{P} \]

我超，斜率+凸包

那么答案查询就是二分斜率找点

接下来考虑修改

发现当修改位置为\(i\)时，对于某些\(j\)，只是给分子或分母的两个\(p\)或\(q\)同时减去一个数，再加上一个数，抵消了，不影响斜率，但值变了，这就是平移

所以对序列分块，每个块建一个包，修改点所在包重构，其余平移即可维护

• 2.

进一步化简\(s_i\)可得：

\[s_i = \frac{1}{PQ} \times (p_iQ - q_iP) \]

没修改的时候就是要最大化后面那坨，然后发现这东西可以使用第三维是\(0\)的向量叉积（？？？？？）

然后还是凸包，还是分块维护

...

参考

2024.7.26

T1 Not Sitting

Tina的选择明显是在四个角，所以计算一下每个格子到四个角的最大距离，排序即可

考场上写的宽搜，就是Rahul肯定是在中间落座，然后逐层向外，典型宽搜

考试时不小心把v打成1了...挂了40

T3 初生的东曦，彼阳的晚意

就black and white那天的题加了个区间查询，这次用了线段树维护直径，因为直径有个性质：合并后直径的端点只可能来自合并前两棵树各自直径的四个端点，证明略，而且这个还比括号序列好理解，好理解就相对好写

但标题是为什么呐

嗯...

code

T2 s

可以组合，可以dp

教练给的dp法没看懂(doge)

组合法原理见这里

code

T4 Everything on It

科技，跳了

大概解释一下：

反演那部分不说了，套的板子，原理还行

重点看\(f_i\)的求法

首先明确\(f_i\)表示选出（钦定）\(i\)个调料出现次数小于等于\(1\)，那么首先就是一个\(\begin{pmatrix}n \\ i\end{pmatrix}\),然后分类

• 钦定部分

这部分可以分为两类：出现一次，没出现

没出现不管，对于出现一次的，设有\(j\)个，此时共\(\begin{pmatrix}i \\ j\end{pmatrix}\)种，让这些调料出现在\(k\)碗面中，方案是第二类斯特灵数，所以单个\(j\)答案是\(\begin{pmatrix}i \\ j\end{pmatrix}\begin{Bmatrix}j \\ k\end{Bmatrix}\),再根据\(j\)的范围，可得答案为\(\sum\limits_{j = 0}^{i}\begin{pmatrix}i \\ j\end{pmatrix}\begin{Bmatrix}j \\ k\end{Bmatrix}\)

但是那\(k\)碗面里还有别的料，这些就随便了，剩了\(n-i\)种料，一碗加不加共\(2^{n-i}\)种，每碗之间相互独立，所以共\(2^k\)种组合

再枚举一下\(k\)

三者相乘得到第一部分

\[\sum\limits_{k = 0}^{i}（2^{(n-i)k}\sum\limits_{j = 0}^{i}\begin{pmatrix}i \\ j\end{pmatrix}\begin{Bmatrix}j \\ k\end{Bmatrix}） \]

• 未钦定部分

这部分简单，加不加\(2^{n-i}\)种，每个加的方法出不出现是二的次方级别，为\(2^{2^{n-i}}\)

然后两部分以及开头的组合乘起来，就是\(f_i\)

2024.7.27

萎了

T3 组合

看到\(Catalan\)，忘了咋求还对应错了情景（悲）

• \(typ = 1\)

就是每时每刻向右走次数不少于向左走次数，裸的\(Catalan\)，然后因为要走回去所以除以2

\[ans = H(\frac{n}{2}) \]

把这对到情景0去了...

• \(typ = 3\)

此时横纵方向都是\(Catalan\)，枚举横向走了多少，然后选出横着走的，再乘上两个方向上的\(Catalan\)即可

\[ans = \sum_{i = 0,i += 2}^{n}C_{n}^{i}H(\frac{i}{2})H(\frac{n-i}{2} ) \]

• \(typ = 0\)

这部分没限制，和卡特兰没关系，同样枚举横向走了几步，然后从横、纵步数中各选出一半向某方向走，剩下的就往相反方向走

\[ans = \sum_{i = 0,i += 2}^{n}C_{n}^{i}C_{i}^{\frac{i}{2}}C_{n-i}^{\frac{n-i}{2}} \]

• \(typ = 2\)

这里比较复杂

设\(dp_i\)表示走了\(i\)步后回到原点，那么枚举中间未经过原点的步数，这些步数只能往一个方向走还不经过原点，是卡特兰，然后又因为四个方向，要\(\times 4\)

\[dp_i = \sum _{j = 0}^{i}4\times dp_{i-j}H(\frac{j}{2}-1) \]

答案\(dp_n\)

code

T2 树

高消有\(30\)，系数就是距离，但是由于系数数组必须用double,所以赋值时要给距离乘一个\(1.0\)

接下来看std:

定义\(sum_u\)表示以\(u\)为根的子树的点权和，\(v\)是\(u\)的一个儿子

根据题目可以得到一个式子：

\[b_v = b_u + sum_1 - 2 \times sum_v \]

原理就是从\(u\)到\(v\)时到\(v\)子树内部点（\(sum_v\)）的距离均会减小\(1\)，到外面点（\(sum_1 - sum_v\)）的距离都会增加\(1\)，所以就有这个式子

然后来看看怎么用它

• \(a \to b\)

\(b\)就是\(sum\)从叶子到某点的叠加，可以开个数组\(dfs\)实现，但是该数组里的只是子树内部\(sum\)的叠加，并不是\(b\)，但是这样可以求出\(b_1\)（整棵树都是他的子树。。。），然后按那个式子\(dfs\)推下去即可

• \(b \to a\)

对于所有非根结点都有上述式子，所以可以得到\(n-1\)个式子，

先变一下形式：

\[b_v = b_u + sum_1 - 2 \times sum_v \]

然后把\(n-1\)个式子累加：

\[\sum^n_{i=1} k_ib_i= (n-1)sum_1 - 2 \times b_1 \]

解释：左边，由于加减不同，所以每个\(k_i\)用来表示系数，但是发现每个式子中父节点(\(u\))的系数为\(-1\)，子节点(\(v\))的系数为\(1\)，可以用此特点\(dfs\)求\(k\)；右边，非根结点的\(sum\)叠加就是\(b_1\)

然后就能求出\(sum_1\)，再结合最初的式子得到\(sum_u\)，进而差分得到点权

code

T4 大dp

原理见这里

code

T1 boss

设\(dp_{i,j}\)表示操作\(i\)次后余数为\(j\)的概率，转移较简单

\[dp_{i,j \times k \operatorname{mod}} = \sum_{j,k = 1}^{\operatorname{mod}-1}dp_{i-1,j}\times num_k \]

\(num_k\)表示\(a\)数组中模\(mod\)余数为\(k\)的数的个数

能拿\(50\)（复杂度\(O(mmod^2)\)）

看到\(m \leqslant 10^9\)，有点矩阵加速的味道

这里的阻碍就在于\(num\)是个\(1 \times (\operatorname{mod} - 1)\)的矩阵，但是快速幂要求矩阵是正方形，难以想到

用矩阵在图上的应用来理解是没有问题的，相当于向\(mod-1\)个方向游走

借助此将\(num\)扩充为正方形，他应该长这样：

\[\begin{bmatrix} a& b & c..\\ b& c & a..\\ c& a &b..\\ ..&..&.. \end{bmatrix}\]

\(mod \leqslant 1000\)，肯定不能拿完整的矩阵搞，其实，直接按着图的套路走就行了，开一个备份数组，每次将\(num\)备份后在\(num\)上跑一个\(mod^2\)更新就行了,复杂度\(O(\log m mod^2)\)

code

2024.7.29

T1 花间叔祖

余数种类最小肯定同余的多，再结合同余条件是差为模数倍数，很容易想到对差分数组求一遍\(\gcd\)，如果\(\gcd\)不为\(1\)就直接输出\(1\)（膜\(\gcd\)），否则直接输出\(2\)（膜\(2\)）

没想到\(2\)能兜\(else\)的底，挂了\(25\)...

code

T2 合并r

想到\(dp\)，状态都出来了，但不会转移

定义\(dp_{i,j}\)表示前\(i\)个数和为\(j\)的方案数

考场上只想到添数法转移，然后就不会搞添\(\frac{1}{2^k}\)的转移，感觉下标都成小数了，就把\(dp\)舍了

后来发现还可以通过给和为\(2j\)的序列除以\(2\)来得到和为\(j\)的序列，那添数只用添\(1\)就行了，其他的小数就是之前添的\(1\)不断除以\(2\)得到的

\[dp_{i,j} = dp_{i-1,j-1} + dp_{i,2j} \]

初始化：\(dp_{i,i} = 1\)，就是全放\(1\)的情况

T3 回收波特

神秘题

一点思路没有，还好暴力给的多点

首先有这么一个结论：

如果两个波特的坐标某时刻是相反数，那么在以后的操作中他们的坐标一直是相反数

证明不难，yy一下就出来了

这就说明，对于对称的部分，我们只维护一半就行了，另一半可以推出来，实现的话可以连边

由于波特太多，有个小\(trick\)是平移原点

查询的时候，就相当于跑链直到回至原点/没映射的点，这里可以使用记忆化优化

code

T4 斗篷

读都读不进去...

（字符串\(s\)）

\(getline(s) ?\)，不对

\(s.getline() ?\)，不对

\(cin.getline(s)\)，还不对

(换成\(char\))

\(getchar(a_{i,j}) ?\)，不对

\(a_{i,j} = getchar() ?\)，对（能运行）但不行（格式不对）

... （玩集贸跳了）

\[{\color{Red} \mathfrak{{\Huge getline(cin,s)}} } \]

\[{\color{Orange} \mathfrak{{\Huge getline(cin,s)}} } \]

\[{\color{Violet} \mathfrak{{\Huge getline(cin,s)}} } \]

暴力戳这里，有注释

还有一点没说就是\(getline\)会读入\(r,c\)那行后面的回车，所以要从\(0\)开始

std:

定义\(L_{x,y},R_{x,y},pre_{x,y}\)为点\((x,y)\)向左上/右上/左最远能延伸多远

对每个点都可以有下图的关系：

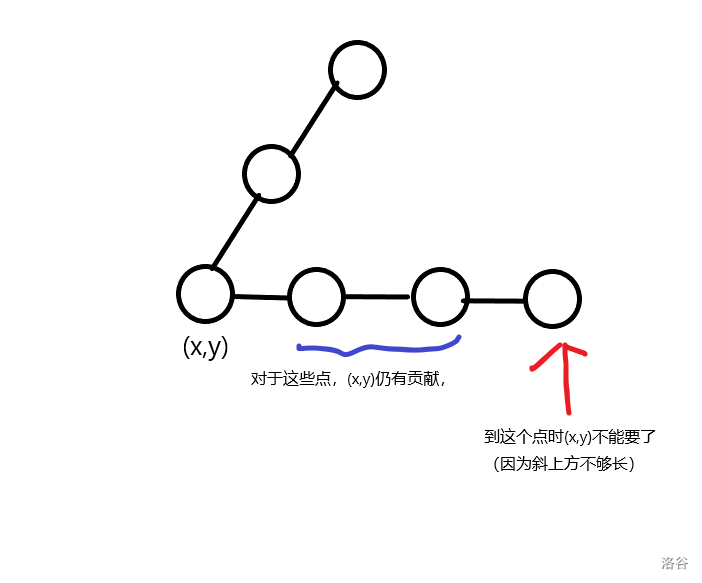
贡献统计可以使用单点加减\(1\)的方法，数据结构用树状数组就够了

代码里应该是把这个图逆时针旋转\(90\)度看的，反正原理一样

还有一点，就是跑一边只能求出正的三角，还需把图反转再跑一遍

80分TLE代码...

2024.7.30

昨天晚上没关空调睡觉结果感冒了，还一直咳嗽，今天只想睡觉...

T1 XOR Matching 2

枚举\(x\)并用它和\(a\)得到对应数组，去和\(b\)比较一下验证是否合法即可，注意去重

code

T2 S

像这个

不同点就是现在求最小次数

同样对最终串\(dp\)，形式基本同那道题，前缀和优化都一样，不同的就是代价那一位用来记录末位是哪个字母(\(0/1/2\))

code

T3 Y

屌题

解析戳这里

T4 O

是这个

难蚌题，目前知道原理但不会写

2024.7.31

咳嗽，呕了一上午

T1 黑客

直接枚举\(x,y\)约去公因数后的数字\(i,j\)，满足\(i + j = z \in [0,999]\)，然后反推出各自可能的公因数取值范围，交集长度就是\(i+j\)出现次数，相乘累加即可

code

T2 密码技术

首先发现行列互不影响，那就是行列方案数乘积

如果\(a,b\)两列能换，\(b,c\)两列能换，那么其实\(a,b,c\)就能自由换(哪怕\(a,c\)不能换)，这样就用并查集处理各个联通块的大小，答案就是\(\prod siz!\)

code

T3 修水管

状压暴力应有45但没改出来

考虑一个大炮

一个水管有漏水可能的前提是前面的水管不是被修了，就是没事儿，考虑从这点出发求解概率

定义\(f_{i,j}\)表示\(r\)轮结束后前\(i\)段修了\(j\)次，前\(i\)段都不会漏水的可能性

对于第\(i\)段，根据上面的说法，他要么在后续的修理中一直没坏，概率为\((1 - p_i)^{r-j}\)，要么坏掉了消耗一次修理次数，概率\(1 - (1 - p_i)^{r-j + 1}\)

所以有

\[f_{i,j} = f_{i- 1,j} \times (1-p_i)^{r-j} + f_{i - 1,j - 1} \times (1 - (1 - p_i) ^{r-j+1}) \]

接着设\(g_i\)表示修理第\(i\)段的概率，那么前\(i-1\)段经过若干次修理后不漏水，然后他自己还得坏掉

\[g_i = (\sum_{j =1}^{r}f_{i-1,j}) \times (1 - (1 - p_i)^{r-j}) \]

最后\(ans = \sum g_id_i\)

code

T4 货物搬运

之前分块有一道入门是单点插入，好像没做

没啥思维，vector + 分块即可

code

还有平衡树写法，不会