[NLP复习笔记] Transformer
1. Transformer 概述
1.1 整体结构
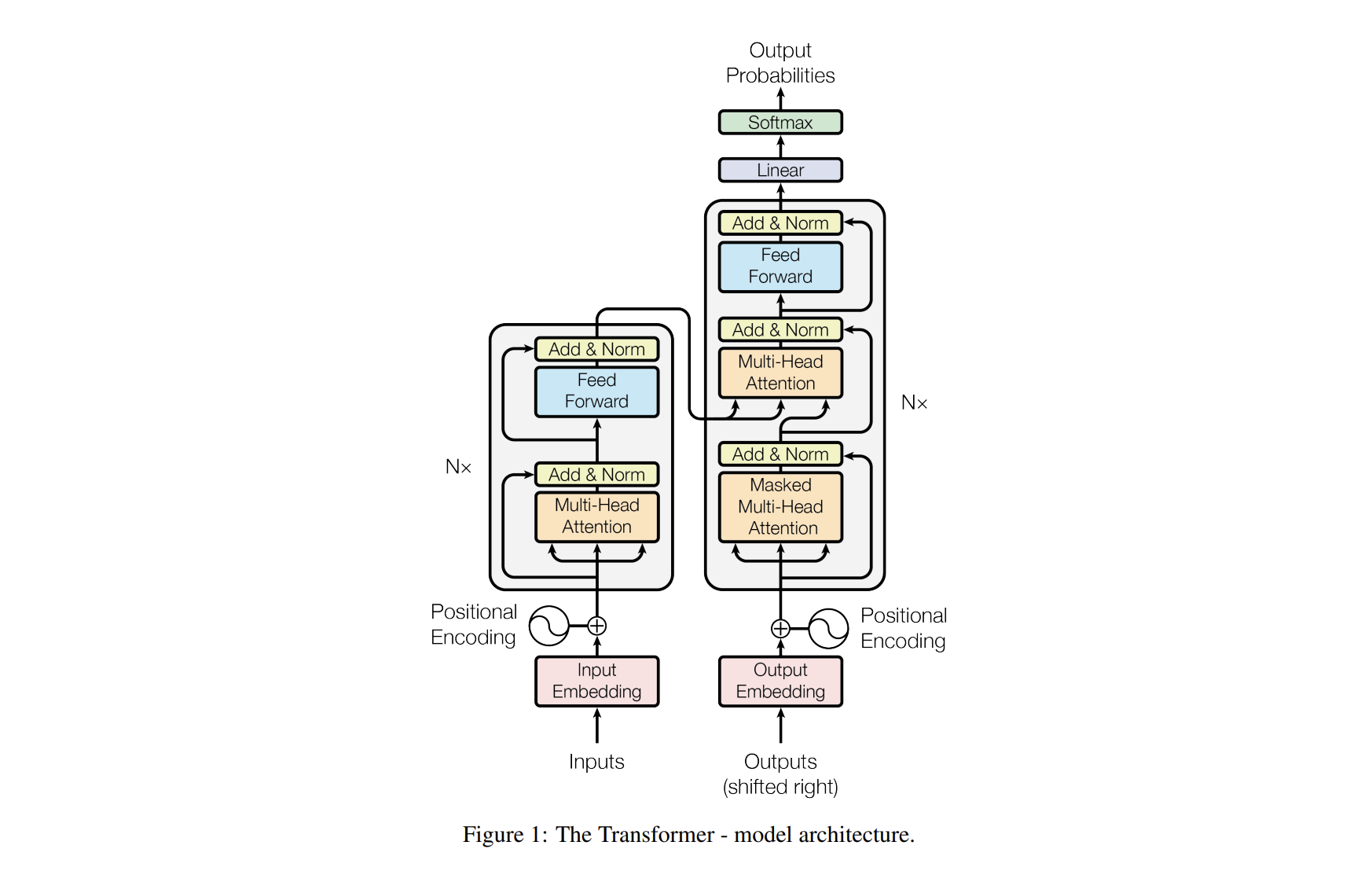
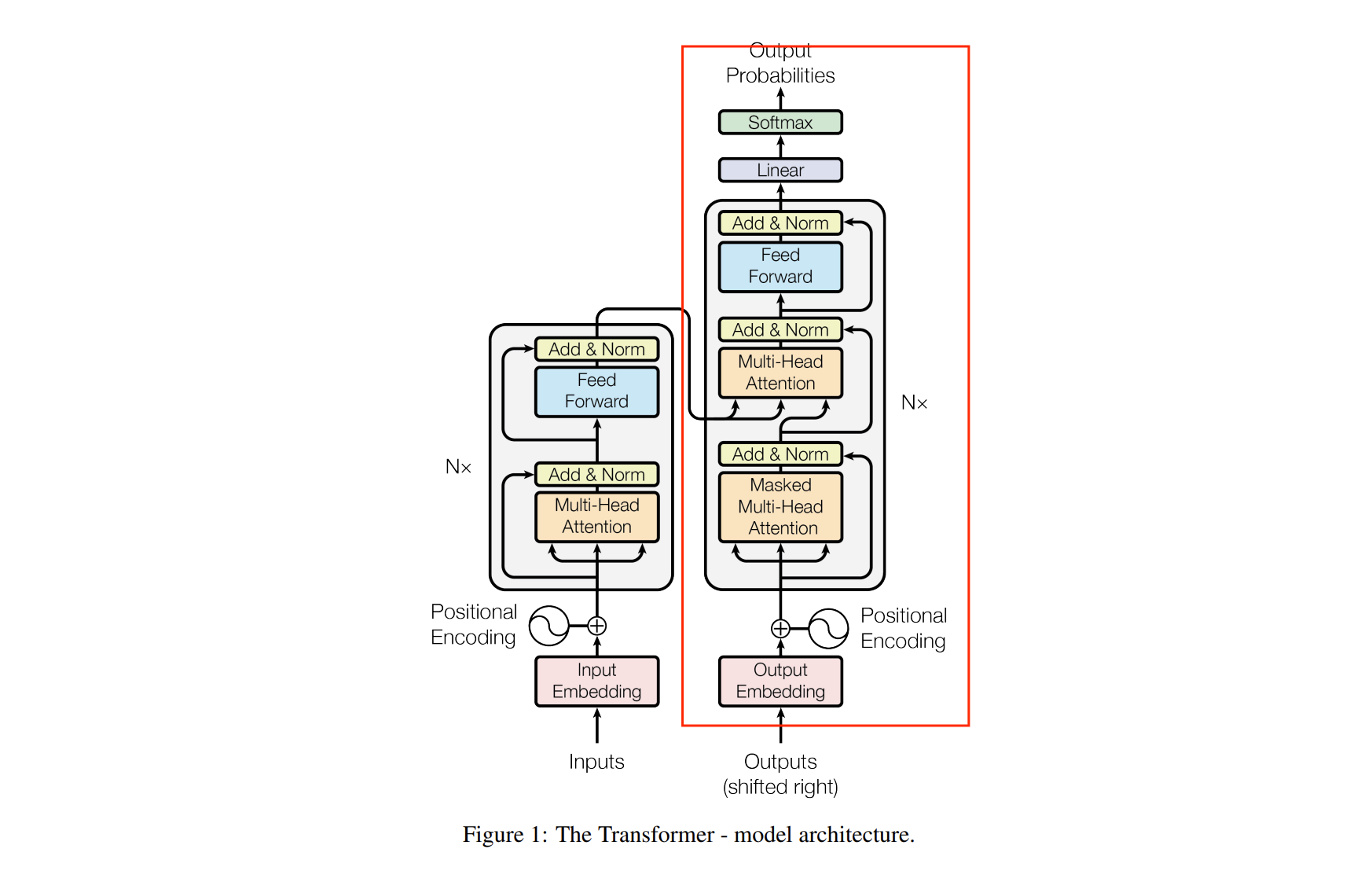
\(\text{Transformer}\) 主要由 \(\text{Encoder}\) 和 \(\text{Decoder}\) 两个部分组成。\(\text{Encoder}\) 部分有 \(N = 6\) 个相同的层,每层包含 一个 \(\text{Muti-Head Attention}\)(多头注意力机制,由多个 \(\text{Self-Attention}\) 组成)和一个 \(\text{Feed-Forword}\);\(\text{Decoder}\) 部分也有 \(N = 6\) 个相同的层,每层包含 两个 \(\text{Muti-Head Attention}\) 和一个 \(\text{Feed-Forword}\) 。
在 \(\text{Encoder}\) 和 \(\text{Decoder}\) 中,每个子层上面还有一个 \(\text{Add \& Norm}\) 层,\(\text{Add}\) 表示 残差连接 (\(\text{Residual Connection}\)) 用于 防止网络退化,\(\text{Norm}\) 表示 \(\text{Layer Normalization}\),用于 对每一层的激活值进行归一化。(残差连接)
在图中,还有模型的输入部分,包括原始输入的词嵌入(\(\text{Input Embedding}\))和标准结果的词嵌入(\(\text{Output Embedding}\)),由 单词 \(\text{Embedding}\) 和 位置 \(\text{Embedding}\) (\(\text{Positional Encoding}\))相加得到。
最后输出,经过一个全连接层和一个 \(\text{softmax}\),得到最终预测的结果 \(O\)。
1.2 简要过程
-
输入 \(X\)
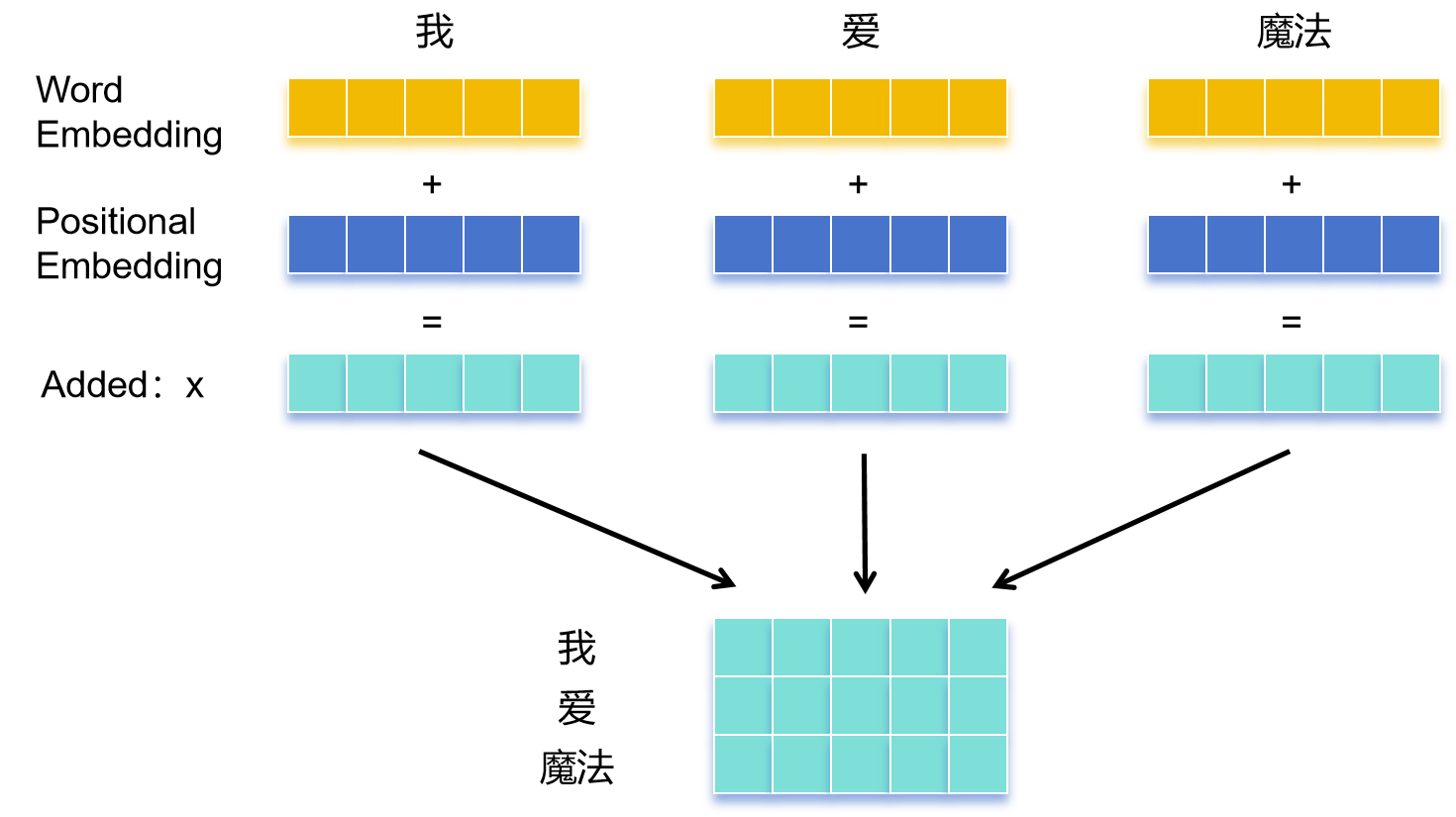
输入序列中的每个单词首先被嵌入(\(\text{Embedding}\))成一个向量,通过 \(\text{Word Embedding}\) 和 \(\text{Positional Embedding}\) 相加 得到这些词向量,并构成输入单词向量矩阵 \(X\)。
(课上学到的 \(\text{Embedding}\) 相关知识,可以看之前整理的一篇随笔 Word Embedding 之 Word2Vec )
-
编码 \(\text{Encoder}\)
将得到的单词表示向量矩阵,传入 \(\text{Encoder}\) 中,经过 \(6\) 个相同的层后得到句子所有单词的编码信息矩阵 \(C\) 。

-
解码 \(\text{Decoder}\)
将 \(\text{Encoder}\) 输出的编码信息矩阵 \(C\) 传递到 \(\text{Decoder}\) 中,\(\text{Decoder}\) 依次根据当前 翻译(预测)过的第 \(1\) 到 \(i\) 个单词 翻译(预测)下一个单词 \(i+1\),也就是说只用到当前单词以及之前的单词,后面的单词需要遮盖住,这个操作称为 \(\text{Mask}\)。
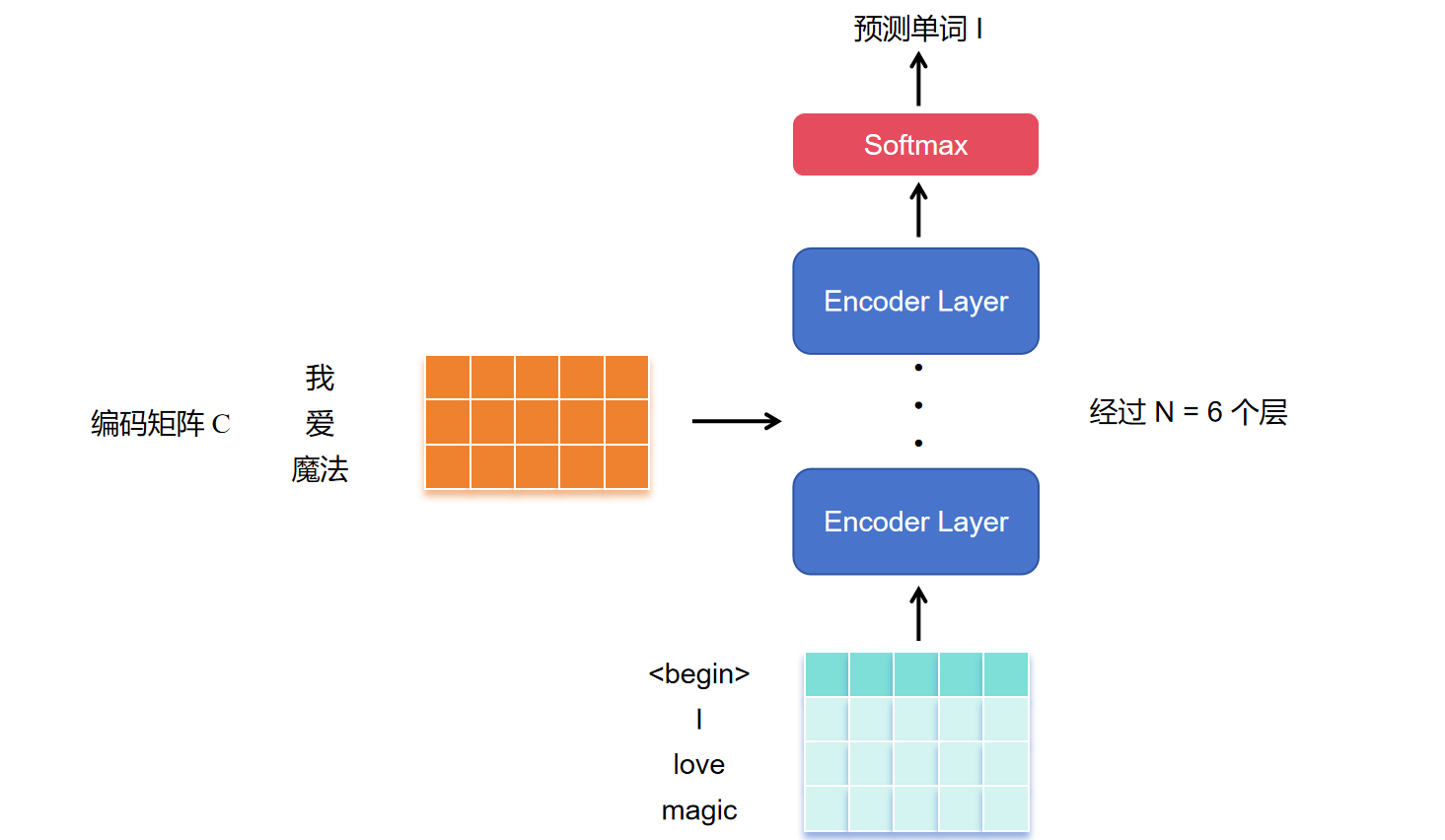
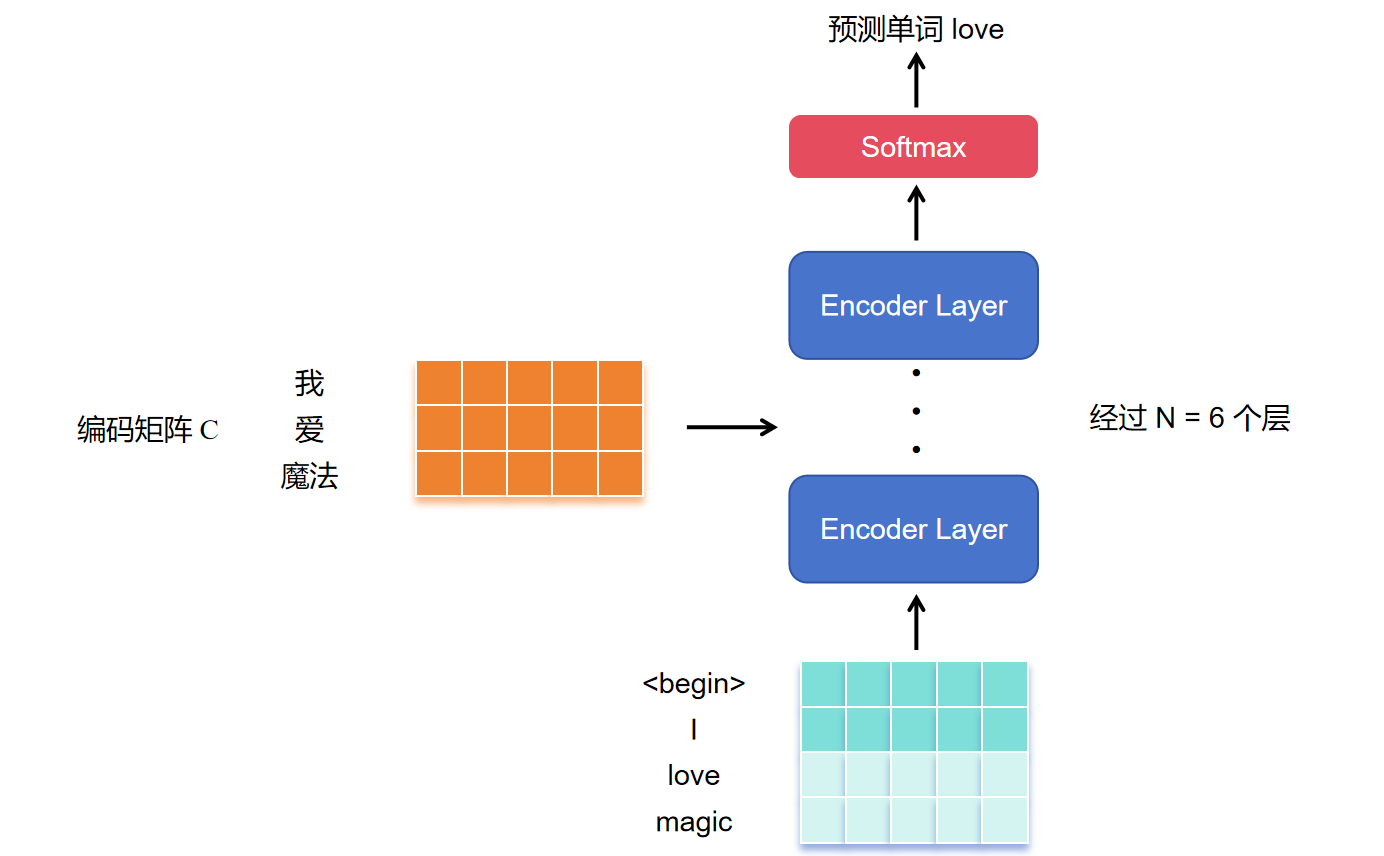
依次类推,最后预测出所有单词。
2. Transformer 输入
2.1 单词 Embedding
单词 \(\text{Embedding}\) 可以通过 \(\text{Word2Vec}\)、\(\text{Glove}\) 等算法预训练得到,也可以在 \(\text{Transformer}\) 中训练得到。
( 词嵌入部分可以看 Word Embedding 之 Word2Vec )
2.2 位置 Embedding
\(\text{Transformer}\) 完全抛弃了 \(\text{RNN}\) 的结构,使用的是全局信息,无法利用单词的顺序信息。 为了使模型能够利用序列的顺序,有必要注入一些关于序列相对位置或绝对位置的信息。
位置 \(\text{Embedding}\) (之后简称 \(PE\))可以通过训练的方式得到,也可以采用某种公式进行计算得到。而 \(\text{Transformer}\) 中通常采用如下公式:
其中,\(pos\) 表示单词在句子中的位置,\(d\) 表示得到的 \(PE\) 的维度(这个维度和生成的词向量的维度是一样的)。\(2i\) 表示偶数维度,\(2i + 1\) 表示奇数维度,并且 \(i \le \frac{d-1}{2}\)。
在论文 《Attention Is All You Need》 中,采用训练 \(\text{Embedding}\) 的方法和采用公式计算的方法,最终得到的结果相近。
并且,公式计算有如下优势:
-
能够适应比训练集里面所有句子更长的句子
假设训练集里面最长的句子是有 30 个单词,若来了一个长度为 31 的句子,则使用公式计算的方法可以直接计算出第 31 个单词对应的 \(PE\)。
-
容易计算出相对位置
对于固定长度的间距 \(k\),\(PE(pos+k)\) 可以用 \(PE(pos)\) 通过变换计算得到。
最后将 \(\text{Word Embedding}\) 和 \(\text{Postianal Embedding}\) 进行一个相加来组成最终的输入词向量 \(X\)。
关于采用这个公式合理性,可以参考这篇文章 Transformer Architecture: The Positional Encoding。
文章中展示了一串序列长度为 50,位置编码维度为 128 的位置编码可视化结果。
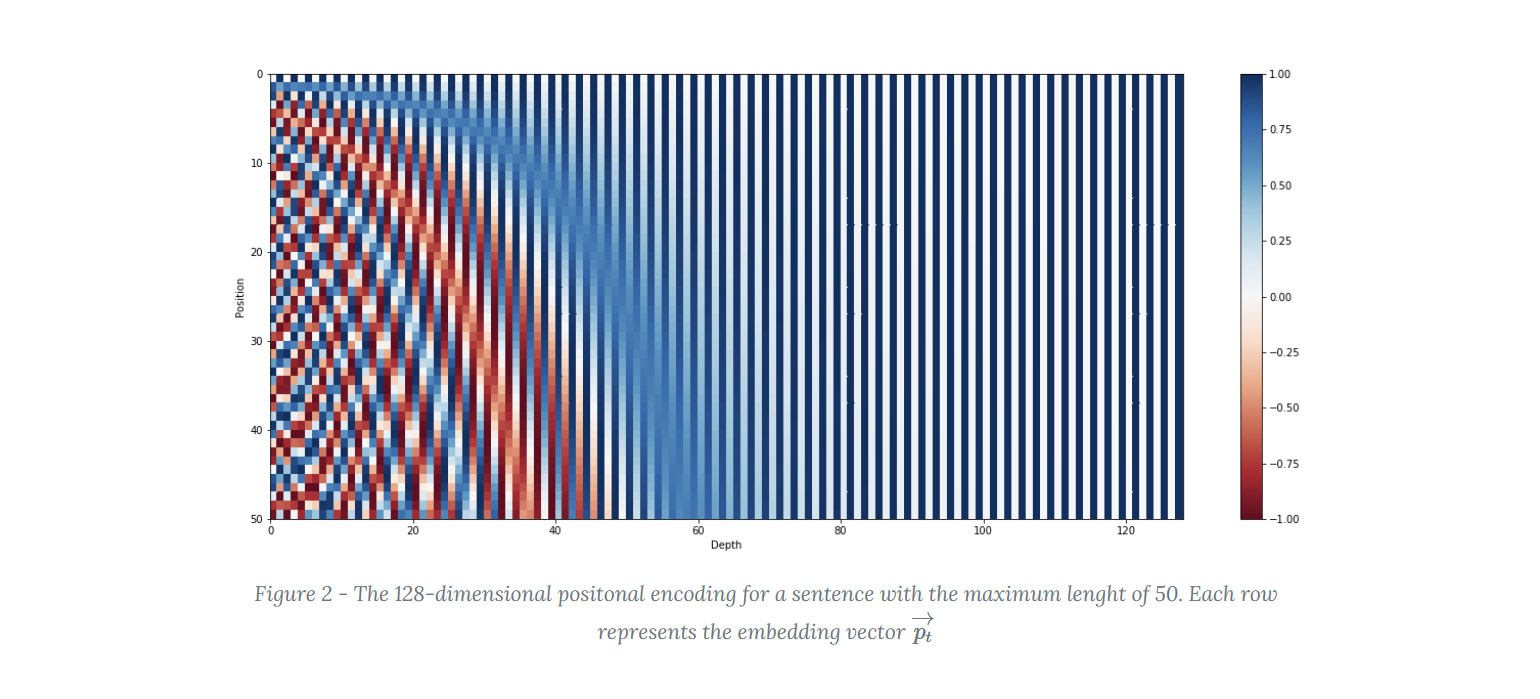
可以发现,三角函数公式使得位置向量的值都位于 \([-1, 1]\) 区间内,值都比较小。
横向来看,对于每个位置 \(pos\),\(pos\) 越靠后,所构成的 \(PE\) 的值波动越多。每个 \(PE\) 都是不同的,表达了不同位置的信息。
纵向来看,对于每个维度 \(i\),\(i\) 越大,频率越小,波长越长,从而导致前面的位置对应的这个维度的值都近乎一样,对于结果的影响也就越小。
3. Self-Attention 自注意力机制
3.1 Self-Attention 简述
自注意力机制(\(\text{Self-Attention}\))是 \(\text{Transformer}\) 中的核心组件之一,使得模型能够在处理序列数据时 更好地捕捉长距离的依赖关系。
在 \(\text{Transformer}\) 中,\(\text{Self-Attention}\) 接收的是输入的词向量矩阵 \(X\) 或者是上一层 \(\text{Encoder}\) 层的输出矩阵。
而关键就在于矩阵 \(Q\)(查询),\(K\)(键),\(V\)(值) 的计算。这些矩阵通过输入 \(\text{X}\) 矩阵线性变换得到。
3.2 Q, K, V 计算
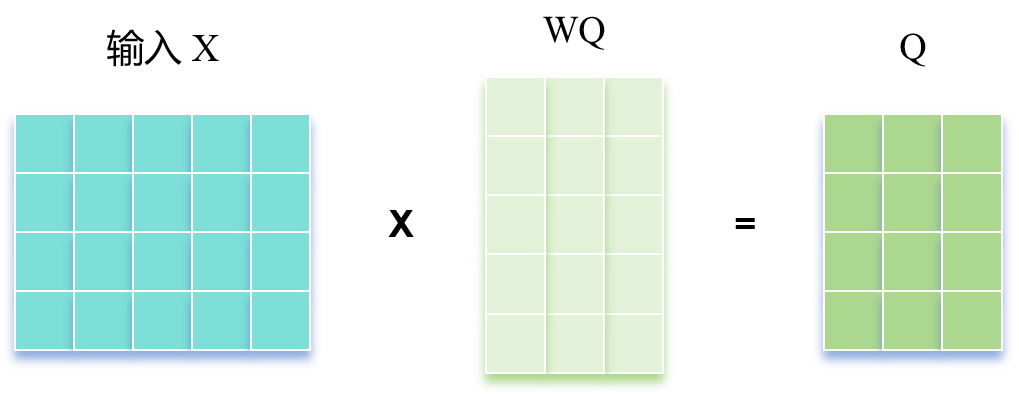
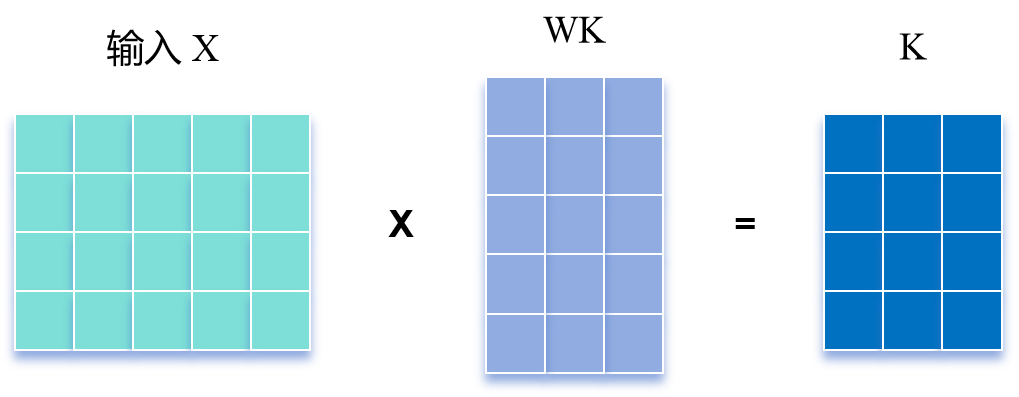
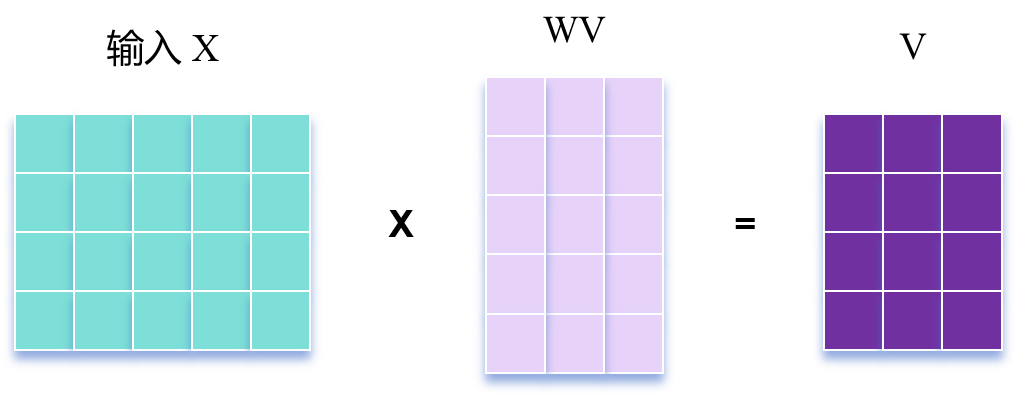
\(\text{Self-Attention}\) 的输入用矩阵X进行表示,则可以使用线性变阵矩阵 \(W^Q\), \(W^K\), \(W^V\) 计算得到 \(Q\), \(K\), \(V\) 。
这里的 \(W^Q\), \(W^K\), \(W^V\) 一般是随机初始化的,随着模型训练一起迭代(就比如可以直接全部设置成一样的,因此此时的 \(Q, K, V\) 也都一样)。
\(X, Q, K, V\) 的每一行向量都表示一个单词。
3.3 Self-Attention 输出
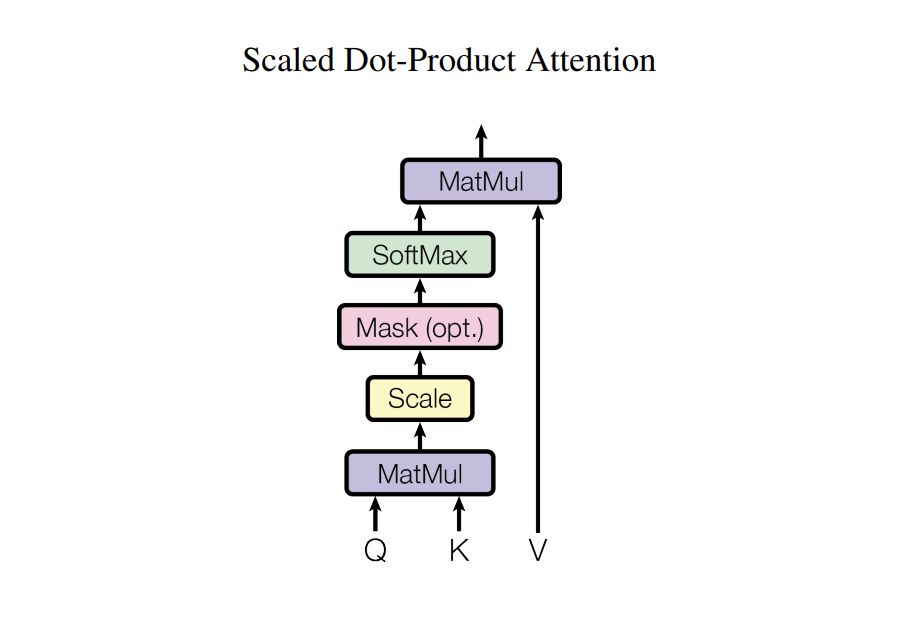
令 \(d_k\) 为矩阵 \(Q\),\(K\) 的列数($Q \in \mathbb{R}^{n \times d_k}, K \in \mathbb{R}^{n \times d_k} $),在输出时,为计算 \(Q\) 和 \(K\) 每一行向量的内积,为了防止内积过大,采取除以 \(\sqrt{d_k}\) 的做法。
其中,内积得到的矩阵 \(QK^T\) 表示的就是 \(n\) 个单词之间的 \(\text{attention}\) 强度。之后再通过一层 \(\text{softmax}\),每一行进行归一化。

最终和 \(V\) 相乘得到输出 \(Z\)。
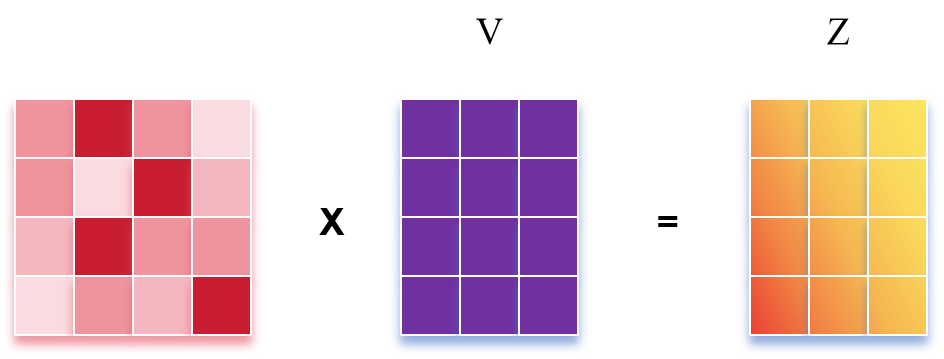
\(Z\) 的每一行为一个单词,\(Z\) 就是当前的输出的编码矩阵。
3.4 Multi-Head Attention 多头注意力机制
但是,单一的自注意力机制会造成缺陷:模型在对当前位置的信息进行编码时,会 过度的将注意力集中于自身的位置。
在论文中,作者提出了通过 多头注意力机制(\(\text{Multi-Head Attention}\))。多头注意力 允许模型在不同位置共同关注来自不同表征子空间的信息,由此来解决注意力过度集中于自身位置这一问题。

所谓的多头注意力机制其实就是 将原始的输入序列拆分进行多组的自注意力处理 过程;然后再将 每一组自注意力的结果拼接 起来进行一次 线性变换 得到最终的输出结果。
其中 \(W^O\) 为线性变换矩阵。\(W^Q_i \in \mathbb{R}^{d_{\text{model}} \times d_k}, \; W^K_i \in \mathbb{R}^{d_{\text{model}} \times d_k}, \; W^V_i \in \mathbb{R}^{d_{\text{model}} \times d_v}, \; W^O \in \mathbb{R}^{hd_v \times d_{\text{model}}}\)。
并且 \(d_k = d_v = d_{\text{model}} / h\)。\(h\) 表示的就是拆分的自注意力模块的个数。\(d_{\text{model}}\) 是之前生成的词向量的维度。
最后输出一个 \(n \times d_{\text{model}}\) 的矩阵,也就是我们通过 \(\text{Encoder}\) 部分每一层多头注意力机制下得到的当前的编码矩阵。
关于多头注意力机制是如何解决注意力过度集中于自身位置的问题,可以参考
为什么Transformer 需要进行 Multi-head Attention
4. Add & Norm 及 Feed Forward
4.1 Add & Norm
在 \(\text{Encoder}\) 部分中每一层多头注意力(\(\text{Muti-head Attention}\))和 \(\text{FeedForward}\) 后面还有一个 \(\text{Add \& Norm}\) 层。
公式如下:
其中, \(X\) 表示 \(\text{Multi-Head Attention}\) 或者 \(\text{Feed Forward}\) 的输入,\(\text{MultiHeadAttention(X)}\) 和 \(\text{FeedForward(X)}\) 表示输出。
\(\text{Add}\) 具体指的是 残差连接,在 \(\text{ResNet}\) 中经常用到。
\(\text{Norm}\) 指 \(\text{Layer Normalization}\),会将每一层神经元的输入都转成均值方差一样,从而可以加快收敛。
4.2 Feed Forward
\(\text{Feed Forward}\) 层比较简单,是 一个两层的全连接层,第一层的激活函数为 \(\text{Relu}\),第二层不使用激活函数,对应的公式如下。
5. Encoder 部分
\(\text{Encoder}\) 部分有 \(N = 6\) 个相同的层,每层包含 一个 \(\text{Muti-Head Attention}\)(多头注意力机制,由多个 \(\text{Self-Attention}\) 组成)和一个 \(\text{Feed-Forword}\)。
经过 \(N = 6\) 个这样相同的层,最终得到输出的单词向量编码矩阵 \(C\) 。

6. Decoder 部分
\(\text{Decoder}\) 部分也有 \(N = 6\) 个相同的层,每层包含 两个 \(\text{Muti-Head Attention}\) 和一个 \(\text{Feed-Forword}\) 。但是在部分结构上与 \(\text{Encoder}\) 存在一些区别:
-
第一个 \(\text{Multi-Head Attention}\) 层采用了 \(\text{Mask}\) 操作。
-
第二个 \(\text{Multi-Head Attention}\) 层的 \(K\), \(V\) 矩阵使用 \(\text{Encoder}\) 得到的 编码信息矩阵 \(C\) 进行计算,而 \(Q\) 使用 上一个 \(\text{Decoder block}\) 的输出 \(Z\) 计算。
-
最后有一个 \(\text{softmax}\) 层,从而得到下一个翻译单词的概率。
\(\text{Decoder}\) 的 \(\text{Multi-Head Attention}\) 采用了 \(\text{Mask}\) 操作。在翻译的过程中是顺序翻译的,即翻译完第 \(i\) 个单词,才可以翻译第 \(i+1\) 个单词。也就是说,翻译第 \(i + 1\) 个单词,只使用前面已经翻译过的第 \(1\) 到 \(i\) 个单词的信息。通过 \(\text{Mask}\) 操作可以防止第 \(i\) 个单词知道 \(i+1\) 个单词之后的信息。
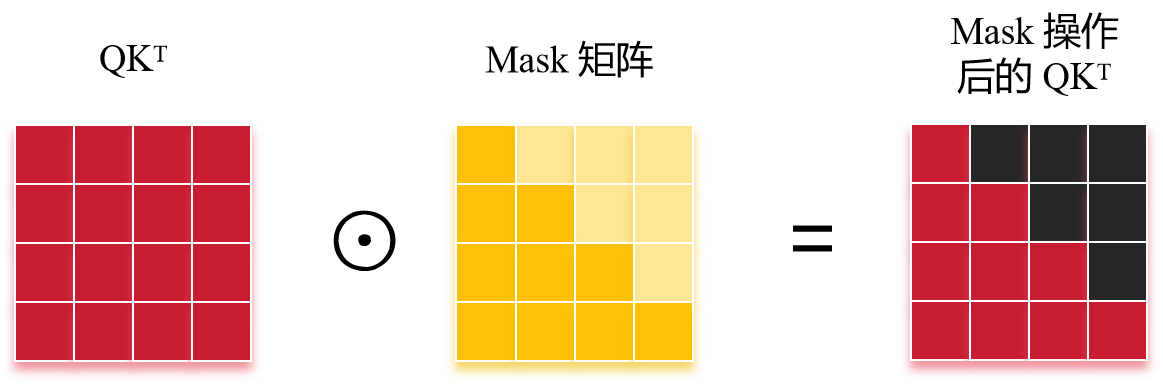
其中 \(\odot\) 表示按位相乘(\(\text{Hadamard}\) 积)。之后还要再做一个 \(\text{softmax}\),\(\text{Mask} \; QK^T\) 的黑色部分表示这两个单词之间的 \(\text{attention score}\) 为 \(0\) 。

显然,此时输出得到的 \(Z\),第一个单词只包含第一个单词的信息,第二个单词只包含第一个进而第二个单词的信息...
之后的操作就和 \(\text{Encoder}\) 中也差不多了,通过 \(\text{Multi-Head Attention}\) 拼接多个输出 \(Z_i\) 然后计算得到第一个 \(\text{Multi-Head Attention}\) 的输出 \(Z\)。
经过多层之后,最终通过一个 \(\text{softmax}\) 得到最终的输出 \(O\),\(O \in \mathbb{R}^{n \times d_{\text{model}}}\)。也就是最终翻译(预测)得到的结果。
参考
Transformer Architecture: The Positional Encoding
为什么Transformer 需要进行 Multi-head Attention?
一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/17958799,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号