[机器学习复习笔记] Linear Regression 线性回归（最小二乘法求解析解）

Linear Regression

1. 一元线性回归

定义一个一次函数如下：

\[y = \theta_0 + \theta_1 x \]

其中 \(\theta\) 被称为函数的 参数。显然在坐标图上，这个函数的图像是一条直线，这也是 线性回归 中的 线性 含义所在。

只有 一个 \(x\) 来预测 \(y\)，就是用一条直线来 拟合 数据，即 一元线性回归。简单地说，一元线性回归就是 找出一条能够通过尽可能多的数据点的直线。

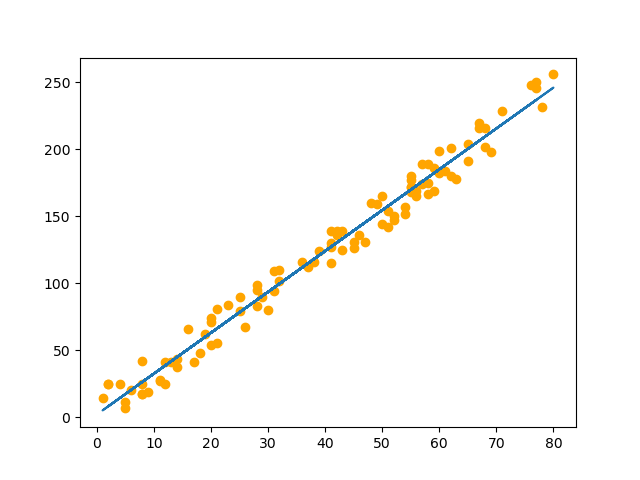
2. 最小二乘法求解一元线性回归

2.1 损失函数

• 残差

  首先引入 残差 的概念，实际指的就是 真实值 与 预测值 之间的 差值，公式如下：

  \[\text{e} = y - \hat y \]

  其中 \(y\) 表示真实值，\(\hat y\) 表示预测值。

• 损失函数

  对于机器学习中的回归问题，残差平方和 是最常用的 损失函数，即 \(\text{SSE}\) （Sum of Squares for Error）：

  \[\hat y_i = \hat \theta_0 + \hat \theta_1 x_i \]
  \[\text{SSE} = \sum_{i = 1}^{n}(y_i - \hat y_i)^2 \]

  其中 \(\hat y_i\) 表示当前第 \(i\) 个样本数据的预测值，\(\hat \theta\) 表示当前预测值下的函数参数，\(n\) 表示样本数据的数量。

  损失函数 是衡量回归模型误差的函数，函数值越小，则说明 拟合程度越高。

  PS：选择残差平方和，是因为平方和可以消除负号。如果仅仅考虑差值之和，那么会出现 负数误差和正数误差抵消 的情况，此时的误差虽然接近于 \(0\)，但明显是不对的；至于为什么不使用绝对值之和，主要是考虑 平方和的微分相对简单，所以一般都使用 残差平方和（\(\text{SSE}\)）。

2.2 最小二乘估计

显然，要使得直线尽可能地拟合数据，需要使得 \(损失函数\) 的值尽可能 小，从而得到 最优的参数 \(\mathbf{\theta}\)。这样一个问题被称为 最优化问题。

为了方便求微分，我们通常用 \(f_{\theta}(x_i)\) 替代 \(\hat y_i\) 来表示 预测值。

为了使得偏微分的形式较为美观，可以在 残差平方和 \(\text{SSE}\) 前 乘 \(\frac{1}{2}\) 。（乘二分之一与否并不会影响参数 \(\mathbf{\theta}\) 的求解）

由以上几点，最终的损失函数 \(E\) 如下:

\[E = \frac{1}{2}\sum_{i=1}^{n}(y_i - f_{\theta}(x_i))^2 \]

显然，损失函数 \(E\) 是一个 凸函数，在一般的一元线性回归问题中，损失函数的图像大致如下：

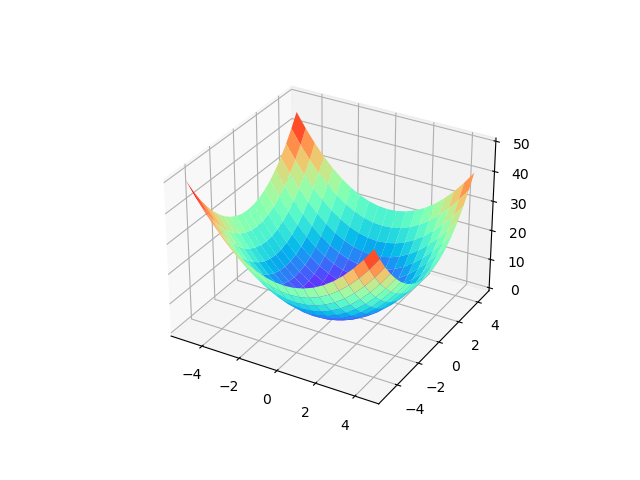
函数的最低点，也就是导数为0取到的点，此时函数值有最小值。所以，分别对 \(\theta_0\) 和 \(\theta_1\) 求偏导数，并令其为0，可以得出参数 \(\mathbf{\theta}\) 的 解析解:

\[\begin{split} \frac{\partial E}{\partial \theta_0} &= \sum_{i = 1}^{n}(f_{\theta}(x_i) - y_i) = 0 \\\\ \frac{\partial E}{\partial \theta_1} &= \sum_{i = 1}^{n}(f_{\theta}(x_i) - y_i)x_i = 0 \end{split} \]

联立上述等式，求解可得：

\[\begin{split} \theta_1 &= \frac{\sum_{i=1}^{n}y_i(x_i - \bar x)}{\sum_{i=1}^{n}x_i^2 - \frac{1}{n}(\sum^{n}_{i=1}x_i)^2} \\\\ \theta_0 &= \frac{1}{n}\sum_{i=1}^{n}(y_i - \theta_1x_i) \end{split} \]

推导过程如下：

\[\begin{split} & 令\; \frac{\partial E}{\partial \theta_0}=0 \; 可得 \quad \theta_0 = \frac{1}{n}\sum_{i=1}^{n}(y_i - \theta_1x_i) \\\\ & 令\; \frac{\partial E}{\partial \theta_1}=0 \; \\\\ & \sum_{i = 1}^{n}(\theta_0 + \theta_1x_i)x_i = \sum_{i=1}^{n}x_iy_i \\\\ &\theta_0 \sum^{n}_{i=1}x_i + \theta_1 \sum_{i=1}^{n}x_i^2 = \sum_{i=1}^{n}x_iy_i \\\\ & 将 \theta_0 代入 \\\\ & \frac{1}{n}\sum_{i = 1}^{n}(y_i - \theta_1 x_i)\sum_{i=1}^{n}x_i + \theta_1 \sum^{n}_{i=1}x^2_i = \sum_{i=1}^{n}x_iy_i \\\\ & \bar x\sum_{i=1}^{n}y_i - \theta_1 \bar x\sum_{i=1}^{n}x_i + \theta_1 \sum^{n}_{i=1}x^2_i = \sum_{i=1}^{n}x_iy_i \\\\ & \theta_1(\sum_{i=1}^{n}x_i^2 - \frac{1}{n}(\sum^{n}_{i=1}x_i)^2) = \sum_{i=1}^{n}y_i(x_i - \bar x) \\\\ & 所以 \; \theta_1 = \frac{\sum_{i=1}^{n}y_i(x_i - \bar x)}{\sum_{i=1}^{n}x_i^2 - \frac{1}{n}(\sum^{n}_{i=1}x_i)^2} \end{split} \]

通过上述推导出的解析解可以直接确定最终的一元线性回归模型。

3. 多元线性回归

在实际生活中，需要解决的问题很多时候是 多变量 的，此时就出现了多个特征，而每个特征也都有对于的参数 \(\theta\)，也就有 多元线性回归：

\[y = \theta_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_dx_d \]

4. 最小二乘法求解多元线性回归

4.1 损失函数的向量化表示

令 \(\mathbf{\theta} = [\theta_0; \; \theta_1; \; \cdots \; \theta_d]\) （ \(\theta\) 是一个大小为 \(d \times 1\) 的列向量），令 \(X\) 为大小为 \(n \times d\) 的数据矩阵。\(y = [y_1; \; y_2; \cdots \; y_n]\) （ \(y\) 是一个大小为 \(n \times 1\) 的列向量，表示 真实值）。
由此可以将 损失函数向量化表示 为:

\[E = \frac{1}{2}(y - X\theta)^T(y - X\theta) \]

其中 \(y\) 为 真实值 ， \(X\theta\) 为 预测值。

4.2 最小二乘估计（多元线性回归）

将 \(E\) 对 \(\theta\) 求偏导：

\[\frac{\partial E}{\partial \theta} = \frac{\partial E}{\partial (y - X\theta)} \frac{\partial(y - X\theta)}{\partial \theta} = (y - X\theta)(- X^T) = X^T(X\theta - y) \]

令偏导数为0，得到多元线性回归的 解析解。但是涉及 求逆 操作，所以分为以下两种情况。

• 当 \(X^TX\) 为 满秩矩阵 或 正定矩阵，则可以直接求得：

\[\theta = (X^TX)^{-1}X^Ty \]

• 当 \(X^TX\) 不是 满秩矩阵，一般是 学习问题包含了多余的特征 或者 存在过多特征 以至于 \(n \le d\) 导致的。对于第一种情况一般的解决方法是 删除一些特征，对于第二章情况，可以删除一些特征，也可以使用 正则化 方法使得一定可逆（这里涉及 岭回归 的知识，暂时不拓展下去）。

通过上述推导求得 解析解 \(\theta\) 来直接确定最终的 多元线性回归模型 。

5. 线性回归（最小二乘法求解析解）核心代码

import numpy as np
from sklearn import datasets

X, y = ...

# 函数
def f(X, theta): 
    return np.dot(X, theta)

# 解析解
def linear_reg(X, y):
    return (X.T * X).I * (X.T * y)

theta = linear_reg(X, y)
y_pred = f(X, theta)

参考文章

线性回归：最小二乘法实现

吴恩达机器学习（十二）正规方程在矩阵不可逆的情况下的解决方法

用人话讲明白线性回归LinearRegression