[数据结构] 稀疏矩阵的转置与快速转置
稀疏矩阵
稀疏矩阵的定义
在矩阵中,若数值为 0 的元素数目远远多于非 0 元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵。
假设在 m * n 的矩阵中,有 t 个非 0 元素,令 δ = t / (m * n) ,则 δ 为矩阵的稀疏因子。
稀疏矩阵的压缩存储
三元组表示法
稀疏矩阵由于非 0 元素很少,所以我们需要压缩存储矩阵。
我们只存储矩阵中的非零元。用 (i, j, e) 来表示一个非零元,其中 i 和 j 表示非零元所在行和列,e 表示非零元的值。稀疏矩阵可以由表示非零元的三元组及其行列数唯一确定。
三元组表示示例
三元组表在存储非零元的时候,首先要按照行序顺序排列,如果行相同,那么需要按照列序顺序排列。
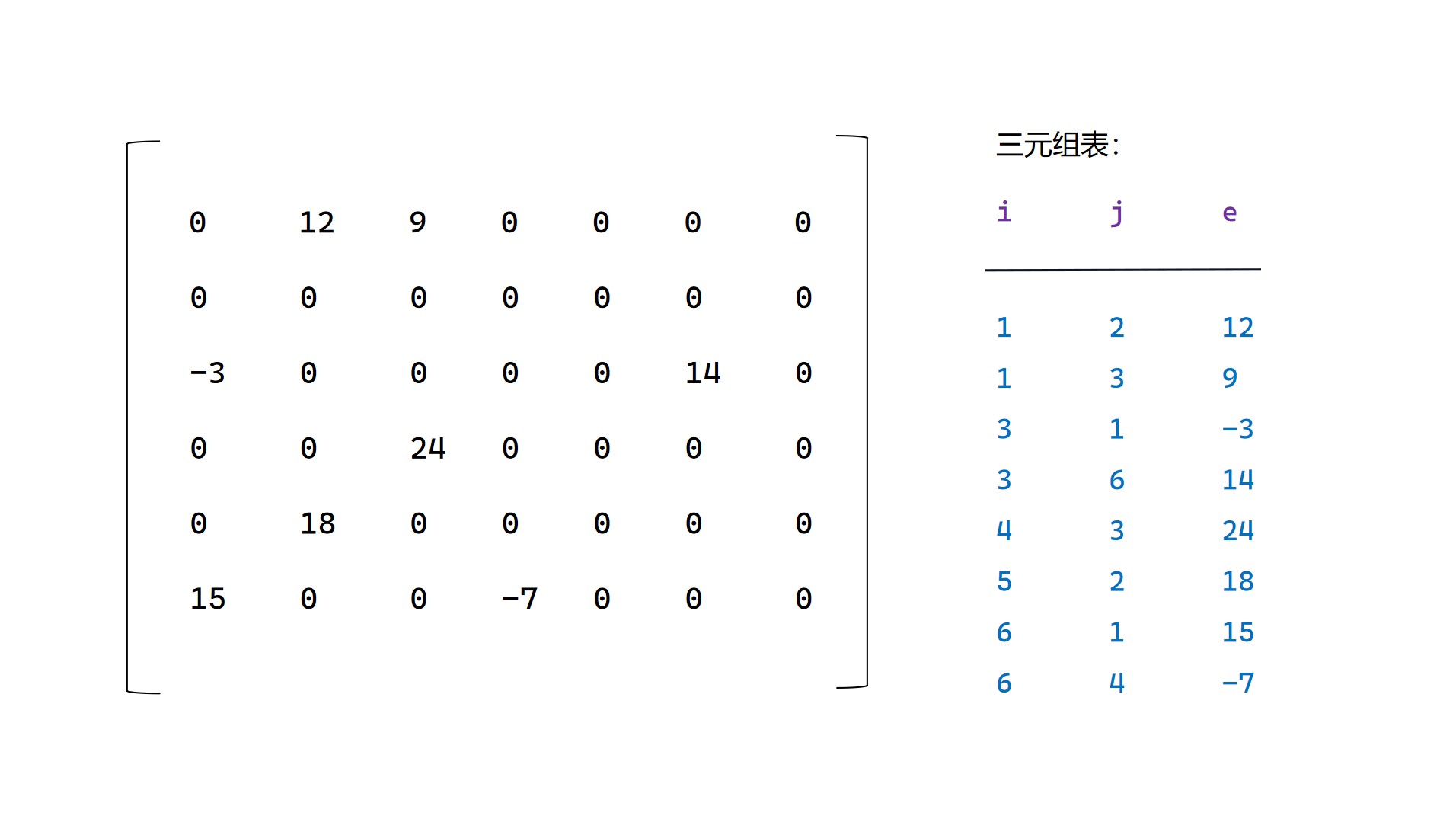
三元组表的基本结构
typedef int ElemType;
typedef struct{
int i, j;
ElemType e;
}Triple;
typedef struct{
Triple data[MAXSIZE];
int mu, nu, tu; //矩阵行数,列数和非0元个数
}TSMatrix;
稀疏矩阵的转置
稀疏矩阵转置的基本概念
转置运算:一个 m * n 的矩阵 M ,其对应的转置矩阵是一个 n * m 的矩阵 T ,并且 T 中的元素 T(i, j) 与 B 中的元素 M(j, i) 对应相等。
我们需要将三元组的行列互换,要构造一个转置矩阵 T 的三元组表,并且这个三元组表中的次序也要满足按照行为主序排列,按照列为次序排列。
由于 T 中的行对应的是 M 中的列,所以在转置过程中,我们需要顺序枚举每一列。
所以朴素的稀疏矩阵转置方法为:
(1)顺序枚举每一列,在矩阵 M 中查找处于该列的非零元三元组;
(2)将该三元组行列互换放入矩阵 T 的三元组表中。
稀疏矩阵转置的结果
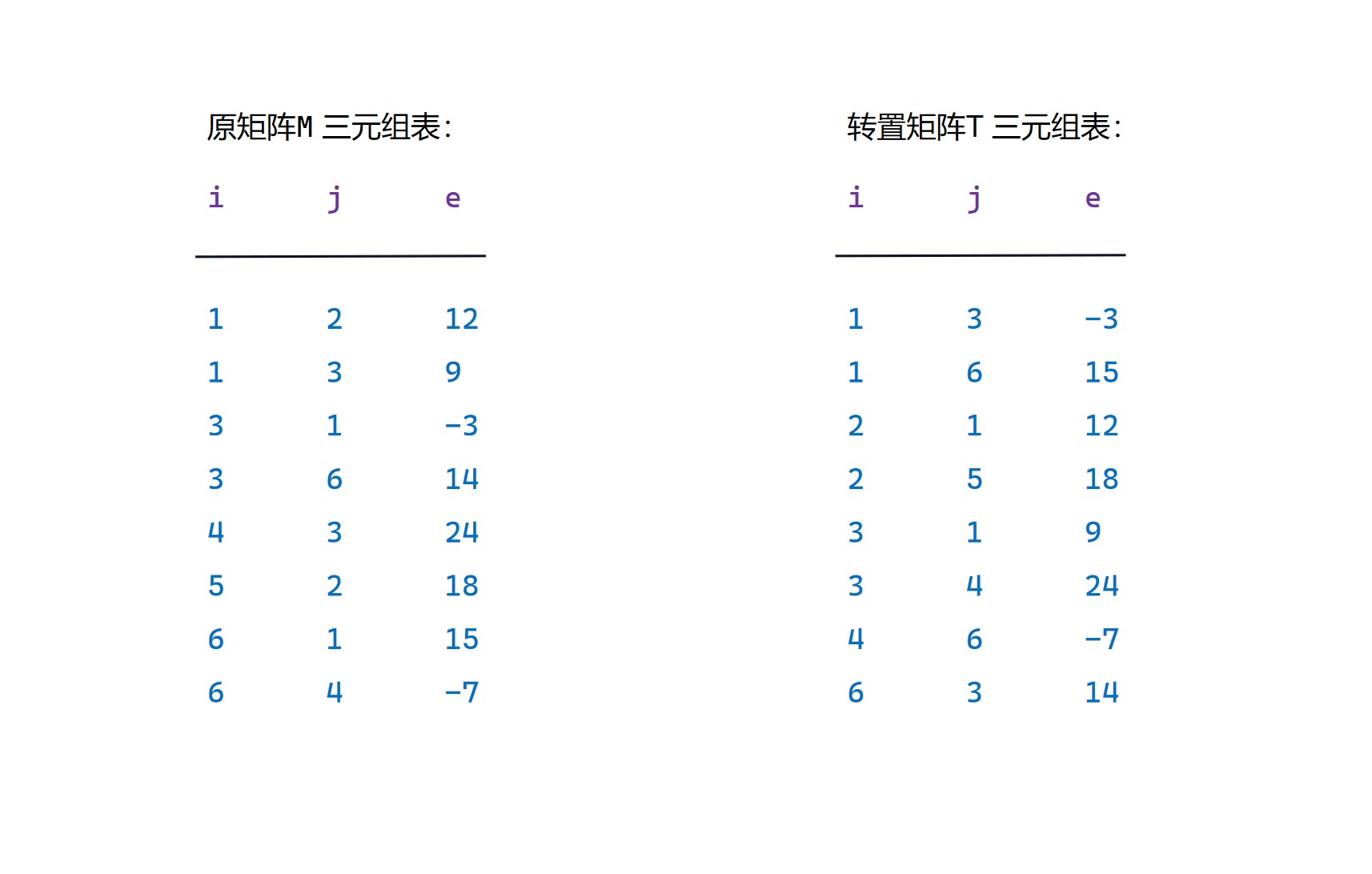
稀疏矩阵转置代码
//稀疏矩阵转置 (适用于 tu << mu × nu 的情况)
void TransposeSMatrix(TSMatrix M,TSMatrix &T){
T.mu = M.nu; //T行数等于原矩阵列数
T.nu = M.mu; //T列数等于原矩阵行数
T.tu = M.tu;
if(!T.tu) return;
int q = 1; //转置矩阵中三元组下标
for(int col = 1; col <= M.nu; ++col){ //枚举每一列
for(int p = 1; p <= M.tu; ++p){ //查找M中处于该列的非零元
if(M.data[p].j == col){
T.data[q].i = M.data[p].j; //互换行列
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
q++;
}
}
}
}
稀疏矩阵的快速转置
稀疏矩阵快速转置的基本思路
朴素的稀疏矩阵转置方法是比较低效的,枚举每一列时都要在原矩阵中的三元组表中扫描一遍,如果可以事先直到每一列的非零元在转置矩阵 T 的三元组表中的对应序号,可以大大减小转置的时间复杂度。
我们可以定义一个数组 num[] 来记录原矩阵 M 中每一列非零元的个数, 同时再定义一个数组 cpot[] 用来记录 M 中每一列第一个非零元在 T 中对应的位置。
在 T 中我们将行列进行了互换,所以在 T 中每一行的第一个非零元对应的是 M 中每一列的第一个非零元。在三元组表中,我们需要按照行主序排列,所以我们要记录 M 中每一列的非零元个数,来知道转置矩阵 T 中每一行的非零元个数,将 M 中同一列的非零元依次排在 T 的三元组表的前面。
为了得到 M 中每一列的第一个非零元在 T 中对应的位置,我们可以得到如下的递推式:

从第二列开始每一列的第一个非零元位置等于前一列的第一个非零元位置加上前一列非零元的个数。
当然第一列可能无非零元,所以 T 中对应位置1有可能延续到后面的某一列中。
稀疏矩阵快速转置代码
//稀疏矩阵的快速转置算法
int cpot[MAXSIZE + 1], num[MAXSIZE + 1]; //辅助数组
//cpot[col] 表示M中第col列第一个非0元在T.data中的位置
//num[col] 表示M中第col列中非0元的个数
void FastTransposeSMatrix(TSMatrix M, TSMatrix &T){
T.mu = M.nu;
T.nu = M.mu;
T.tu = M.tu;
if(!T.tu) return;
for(int col = 1; col <= M.mu; col++)
num[col] = 0; //初始化为0
for(int k = 1; k <= M.tu; k++)
num[M.data[k].j]++; //记录M三元组表每一列列中非0元个数
cpot[1] = 1; //初始化第一个非0元的序号
for(int col = 2; col <= M.mu; col++) //求第col列中第一个非零元在T三元组表中的序号
cpot[col] = cpot[col - 1] + num[col - 1];
for(int p = 1; p <= M.tu; p++){
int col = M.data[p].j; //此时M对应三元组中的非0元的所在列
int q = cpot[col]; //q为当前非0元的应当放置的序号位置
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
cpot[col]++; //cpot[col]++,对应下一个此列中非0元的序号
//cpot[col]最后一直加到等于cpot[col + 1],第col列也就不会有更多的非0元了
}
}
程序测试
完整程序
点击查看代码
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10000
typedef int ElemType;
typedef struct{
int i, j;
ElemType e;
}Triple;
typedef struct{
Triple data[MAXSIZE];
int mu, nu, tu; //矩阵行数,列数和非0元个数
}TSMatrix;
//输入稀疏矩阵数据
void InPutM(TSMatrix &M){
printf("输入稀疏矩阵的 行数, 列数, 非0元个数 :\n");
scanf("%d %d %d", &M.mu, &M.nu, &M.tu);
printf("输入矩阵非0元素的 所在行i, 所在列j, 值e:\n");
for(int k = 1; k <= M.tu; k++){
scanf("%d %d %d", &M.data[k].i, &M.data[k].j, &M.data[k].e);
}
}
//打印稀疏矩阵三元组数据
void PrintM(TSMatrix T){
printf(" %d %d %d\n", T.mu, T.nu, T.tu);
printf(" ------------\n");
for(int k = 1; k <= T.tu; k++){
printf(" %d %d %d\n",T.data[k].i, T.data[k].j, T.data[k].e);
}
}
//稀疏矩阵转置 (适用于 tu << mu × nu 的情况)
void TransposeSMatrix(TSMatrix M,TSMatrix &T){
T.mu = M.nu; //T行数等于原矩阵列数
T.nu = M.mu; //T列数等于原矩阵行数
T.tu = M.tu;
if(!T.tu) return;
int q = 1; //从列数小的开始,一一对应赋值
for(int col = 1; col <= M.nu; ++col){
for(int p = 1; p <= M.tu; ++p){
if(M.data[p].j == col){
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
q++;
}
}
}
}
//稀疏矩阵的快速转置算法
int cpot[MAXSIZE + 1], num[MAXSIZE + 1]; //辅助数组
//cpot[col] 表示M中第col列第一个非0元在T.data中的位置
//num[col] 表示M中第col列中非0元的个数
void FastTransposeSMatrix(TSMatrix M, TSMatrix &T){
T.mu = M.nu;
T.nu = M.mu;
T.tu = M.tu;
if(!T.tu) return;
for(int col = 1; col <= M.mu; col++)
num[col] = 0; //初始化为0
for(int k = 1; k <= M.tu; k++)
num[M.data[k].j]++; //记录M三元组表每一列列中非0元个数
cpot[1] = 1; //初始化第一个非0元的序号
for(int col = 2; col <= M.mu; col++) //求第col列中第一个非零元在T三元组表中的序号
cpot[col] = cpot[col - 1] + num[col - 1];
for(int p = 1; p <= M.tu; p++){
int col = M.data[p].j; //此时M对应三元组中的非0元的所在列
int q = cpot[col]; //q为当前非0元的应当放置的序号位置
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
cpot[col]++; //cpot[col]++,对应下一个此列中非0元的序号
//cpot[col]最后一直加到等于cpot[col + 1],第col列也就不会有更多的非0元了
}
}
int main(){
TSMatrix M, T, FT;
printf("————稀疏矩阵转置测试————\n\n");
InPutM(M);
printf("\n稀疏矩阵转置前三元组: \n");
PrintM(M);
printf("\n稀疏矩阵转置结果: \n");
TransposeSMatrix(M, T);
PrintM(T);
printf("\n稀疏矩阵的快速转置结果: \n");
FastTransposeSMatrix(M, FT);
PrintM(FT);
}
测试结果

一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/17111815.html,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号