[数据结构] 二分查找 (四种写法)

二分查找

二分查找

二分查找（Binary Search）也叫作折半查找，前提是查找的顺序结构是有序的，我们一般在数组上进行二分查找。
二分查找就好像猜数字大小游戏一样。假设要数字目标值属于 [1, 1000] 范围内，当我们猜的数字小于这个目标值时（"Too low"），我们需要往大去猜；反之大于这个目标值时（"Too high"），我们需要往小去猜。当然这里猜的方式并不是盲目的，我们每次都取中间值去猜，每猜一次可以缩小当前一半的范围，这样可以大大提高效率。二分查找本质上也是这样的过程，时间复杂度为 O(logn) ，在较大数据情况下相比线性查找要快非常多。

我们定义一个左指针 left 标记当前查找区间的左边界，一个右指针 right 标记当前查找范围的右边界。每次取 mid 来判断当前取的值是否等于目标值 target。如果等于 target 就直接返回 mid ；如果小于目标值 target ，那么将左边界变为 mid + 1，缩小区间范围继续在 [mid + 1, right] 范围内进行二分查找，如果大于目标值 target ，那么将右边界变为 mid - 1，缩小区间范围继续在 [left, mid - 1] 范围内进行二分查找。

假如最后出现了 left > right 的情况，说明区间范围大小缩小到 0 都无法找到该目标值，那么很明显数组中不存在这个目标值 target，此时退出循环，返回 -1 。

二分查找图解

（1）

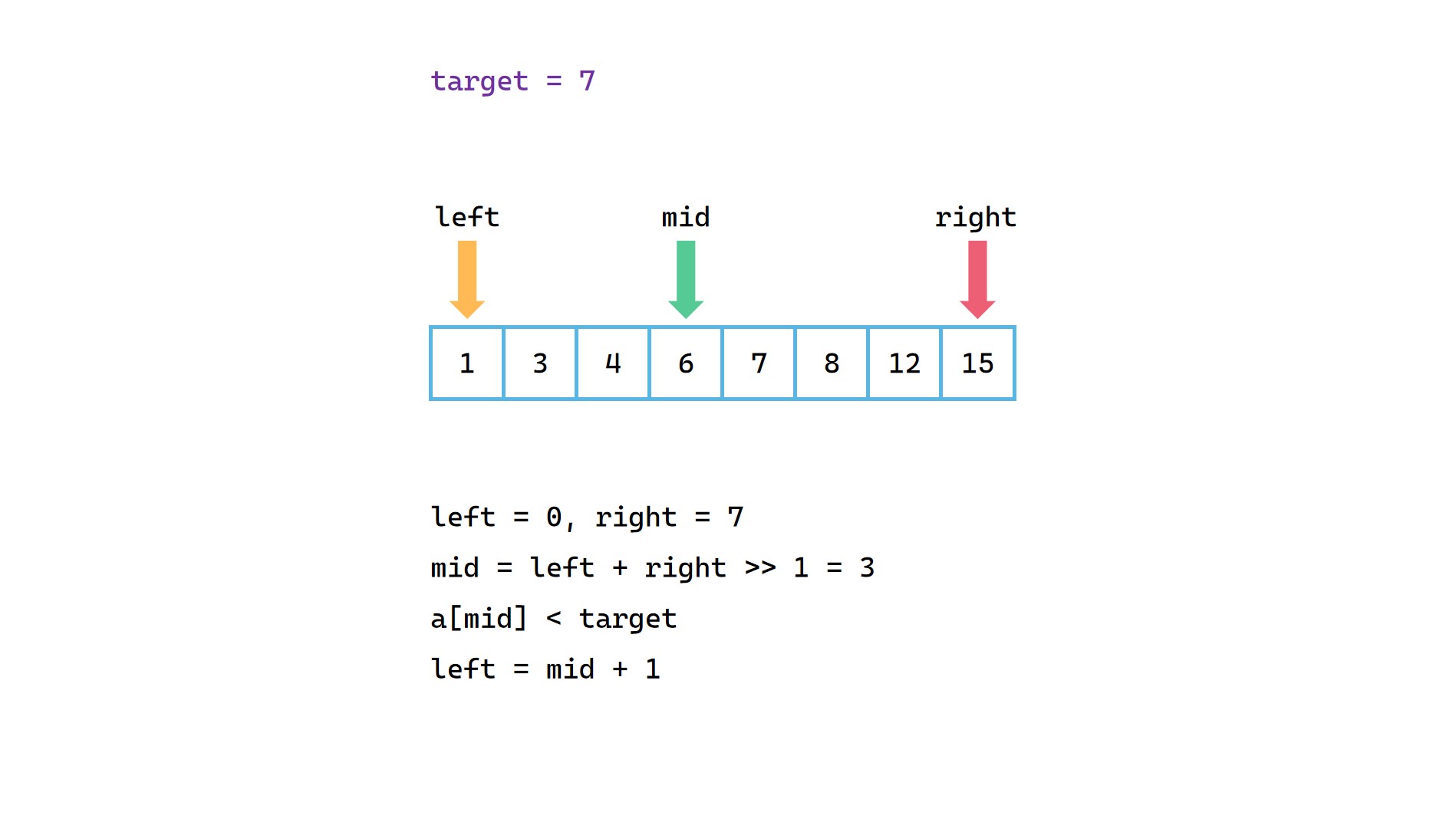
（2）

（3）

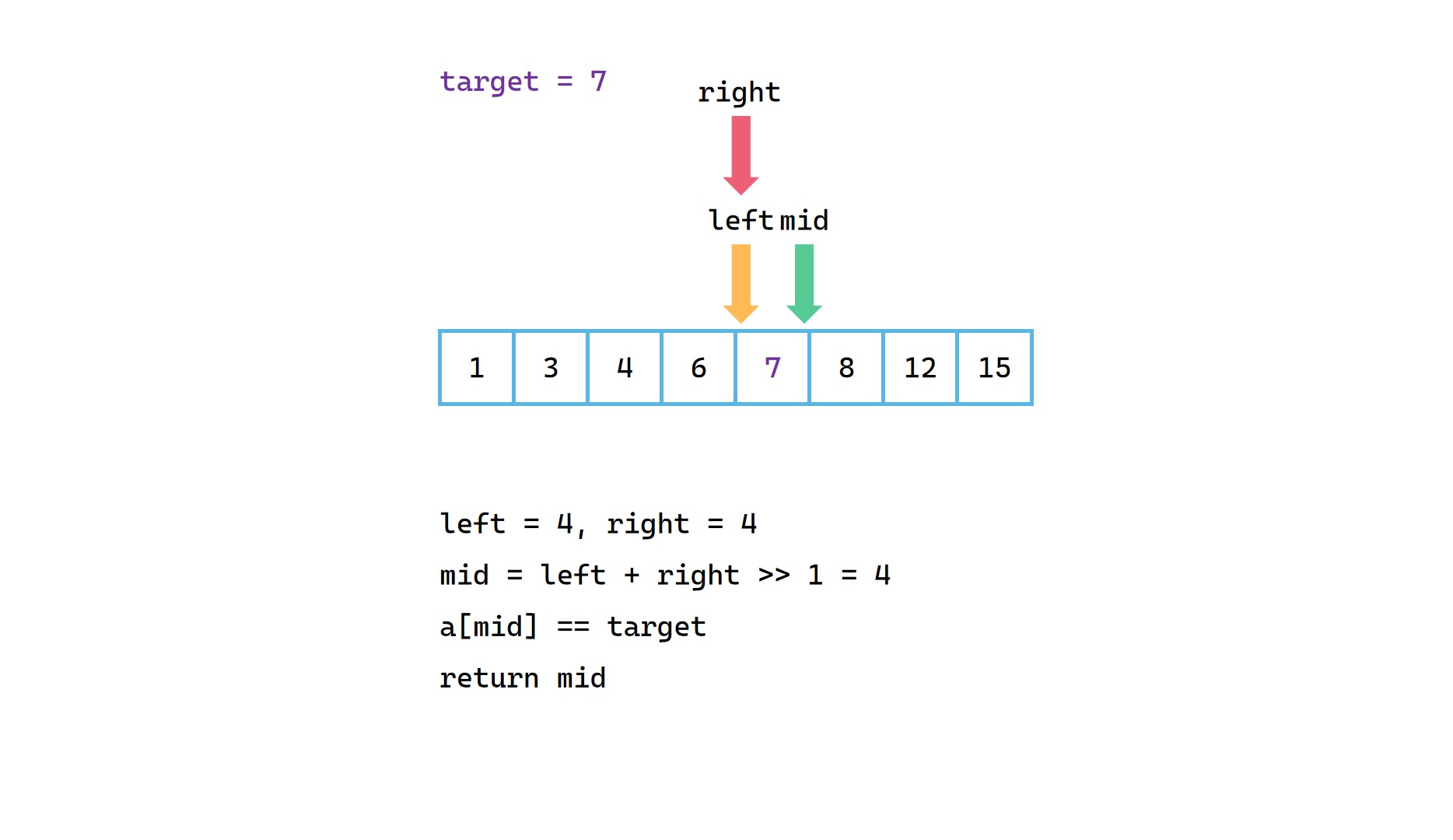
二分查找代码

//二分查找
int BinarySearch(vector<int> &v, int target){
    int left = 0, right = v.size() - 1;
    while(left <= right){
        int mid = (left + right) >> 1;
        if(v[mid] == target)
            return mid;
        if(v[mid] < target)
            left = mid + 1;
        else
            right = mid - 1;
    }
    return -1;
}

---

二分查找 递归

上面二分查找也可以写成递归的形式。大致步骤为：
（1）当前层 mid 位置元素等于目标值 target，直接 return mid；
（2）如果小于目标值，递归搜索 [mid + 1, right] 范围；
（3）如果大于目标值，递归搜索 [left, mid - 1] 范围。

//二分查找法递归写法
int BinarySearchRec(vector<int> &a, int left, int right, int target) {
    int mid = (left + right) >> 1;
    if(left <= right){
        if(a[mid] == target)
            return mid;
        if(a[mid] < target)
            return BinarySearchRec(a, mid + 1, right, target);
        else
            return BinarySearchRec(a, left, mid - 1, target);
    }
    return -1;
}

---

二分查找 元素起始位置

查找等于目标值的第一个位置

数组中可能存在连续的多个位置元素都等于目标值 target ，当我们要查找第一个出现的位置，我们需要保证查找到位置的左边所有元素都满足小于 target，右边所有元素都满足大于等于 target。

当出现 a[mid] < target 时，说明我们要查找的位置一定在 [mid + 1, right] 范围内，当然也可以写成 (mid, right] ；当出现 a[mid] >= target 时，说明要查找的位置有可能是当前的 mid，也有可能是当前 mid 左边的某个位置，所以此时要查找的位置一定在 [left, mid] 范围内。

因此，当 a[mid] < target，将 left = mid + 1 ；当 a[mid] >= target，将 right = mid。
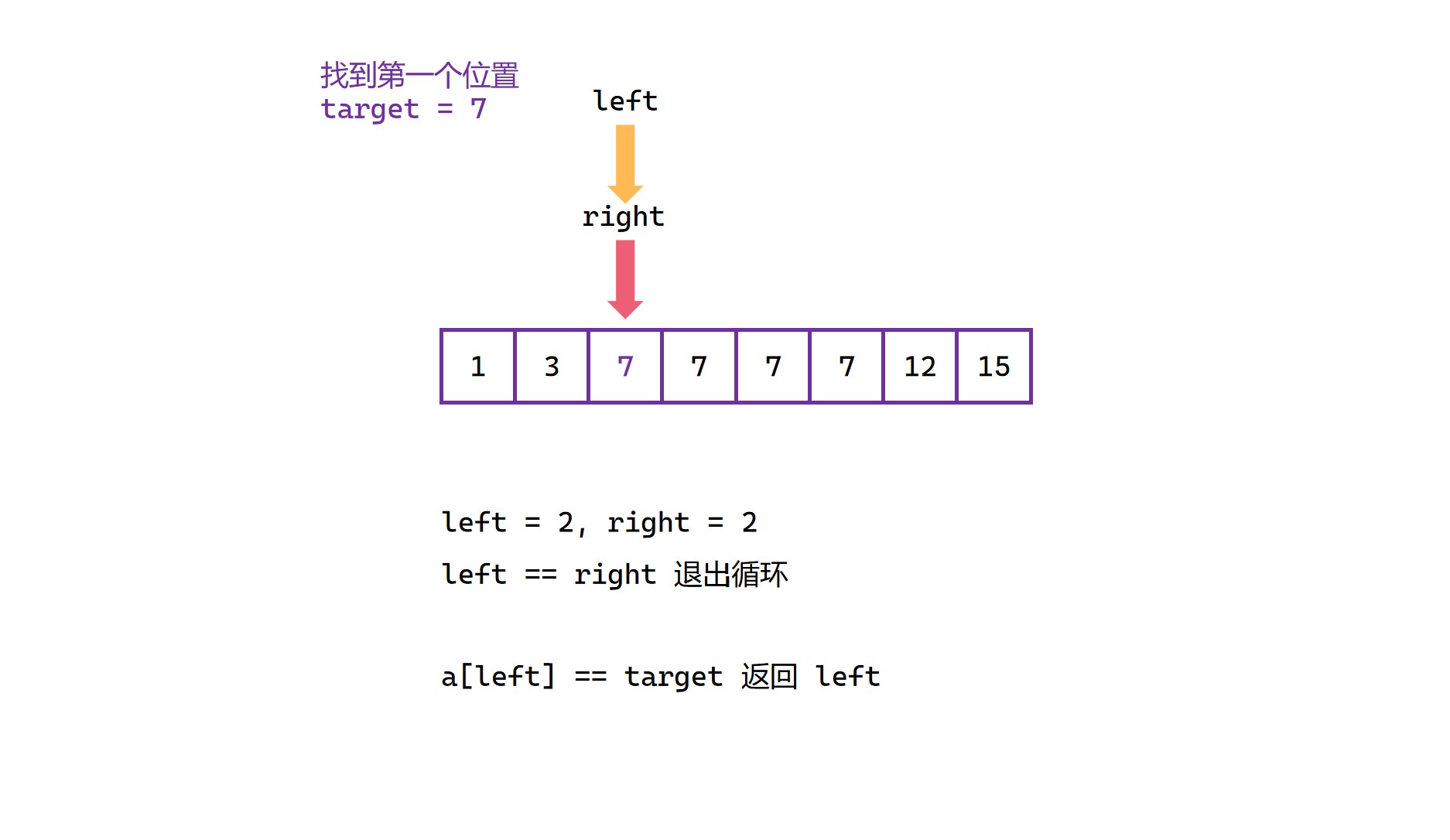
当最后 left == right 即两个指针相遇时退出循环，最后要判断一下相遇位置处的元素是否等于目标值 target。如果等于目标值，就返回 left 或者 right，如果不等于目标值，说明不存在该元素，那么就返回 -1 。

查找等于目标值起始位置图解

（1）

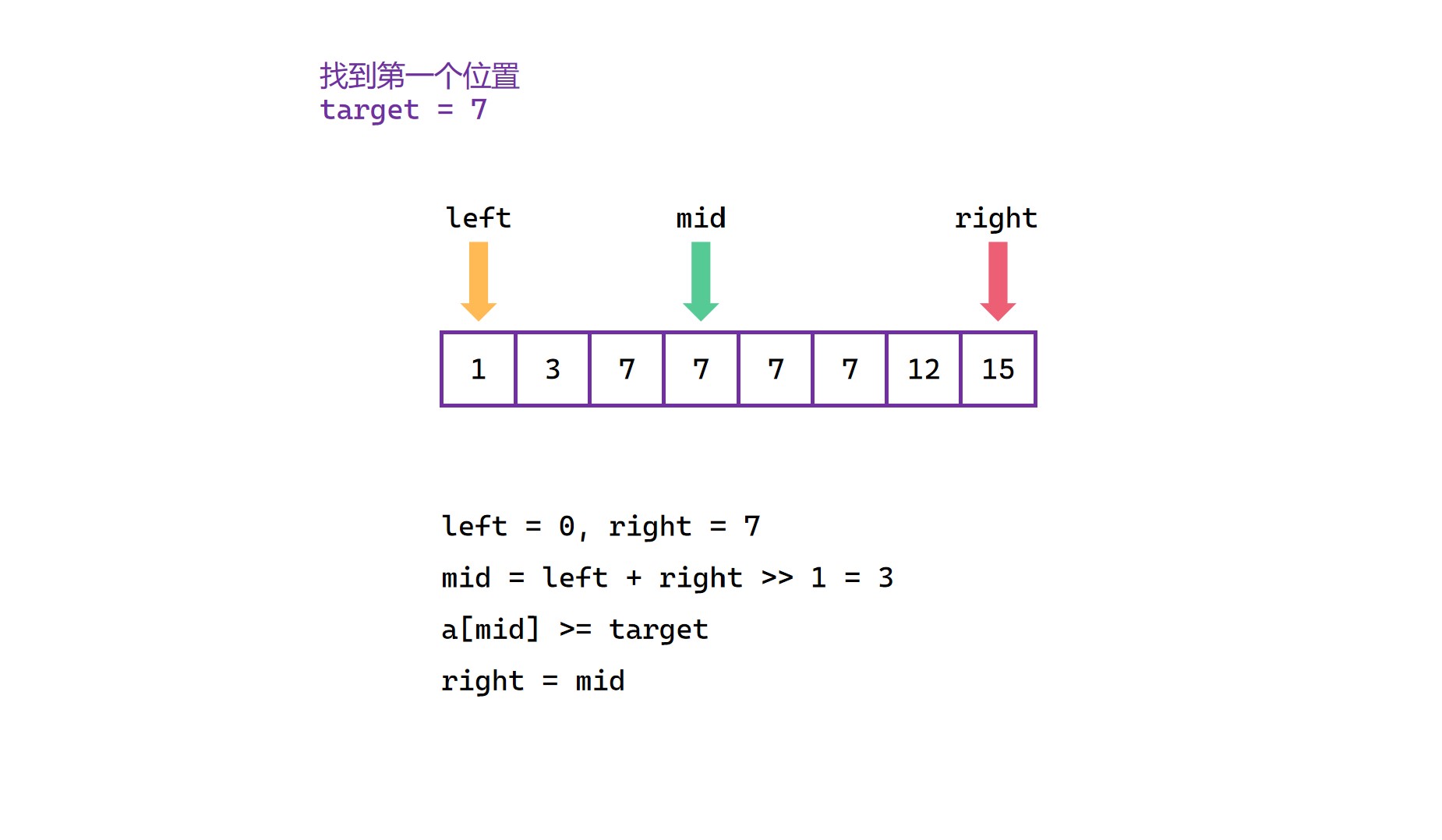
（2）

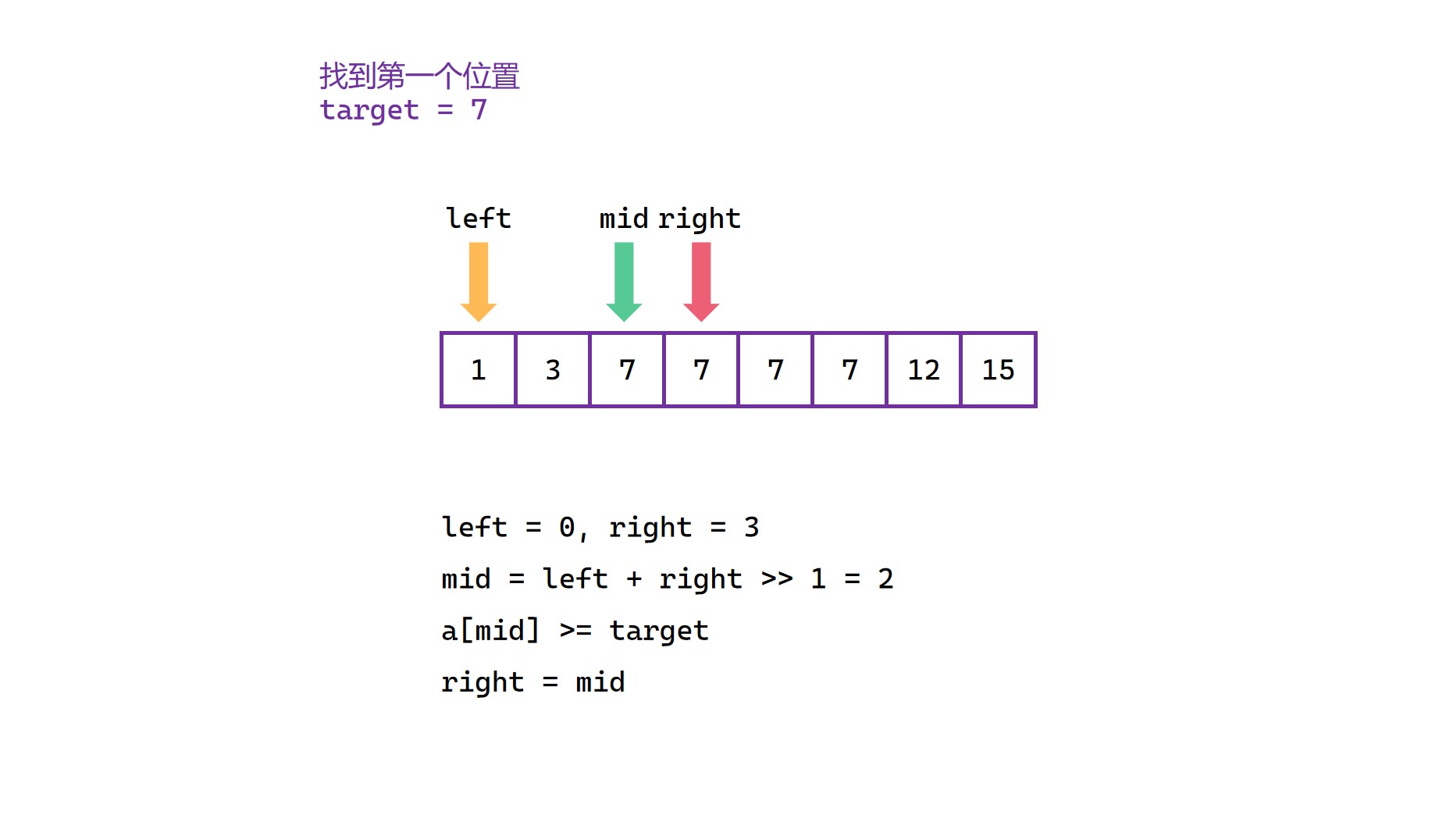
（3）

（4）

查找等于目标值起始位置代码

int BinarySearchfirst(vector<int> &v, int target){
    int left = 0, right = v.size() - 1;
    while(left < right){
        int mid = (left + right) >> 1;
        if(v[mid] < target)
            left = mid + 1;
        else
            right = mid;
    }
    return v[left] == target ? left : -1;
}

---

二分查找 元素终止位置

查找等于目标值的最后一个位置

当我们要查找最后一个出现的位置，我们需要保证查找到位置的左边所有元素都满足小于等于 target，右边所有元素都满足大于 target。

当出现 a[mid] > target 时，说明我们要查找的位置一定在 [left, mid - 1] 范围内，当然也可以写成 [left, mid) ；当出现 a[mid] <= target 时，说明要查找的位置有可能是当前的 mid，也有可能是当前 mid 右边的某个位置，所以此时要查找的位置一定在 [mid, right] 范围内。

因此，当 a[mid] > target，将 right = mid - 1 ；当 a[mid] <= target，将 left = mid。
当最后 left == right 即两个指针相遇时退出循环，最后要判断一下相遇位置处的元素是否等于目标值 target。如果等于目标值，就返回 left 或者 right，如果不等于目标值，说明不存在该元素，那么就返回 -1 。

但是要注意的是，在这里取 mid 时，我们不能和之前一样取 (left + right) >> 1，而要采取 (left + right + 1) >> 1 的形式。我们可以假设只有数组两个元素，两个元素都等于目标值，显然此时我们要找的最后一个位置为下标1。我们模拟一下，初始情况下 left 为 0，right 为 1，如果采用 (left + right) >> 1，那么此时的 mid 就等于 0，这个时候出现了 left 依旧等于之前 left 的情况，那么显然这个时候区间无法进行缩小，left 会一直等于 0，这个时候就陷入死循环了。

我们仔细看一下，当前这种情况的特点是 left + 1 == right，那么我们取 mid 时:
mid = (left + right) >> 1 = (2 * left + 1) >> 1 = left，很明显left 会一直等于 mid。
如果我们能够让 left 在这种 left + 1 == right 情况下使得 left 取到 right 即往后一位，那么我们的区间范围就得以缩小，也不会陷入死循环。所以我们采用 (left + right + 1) >> 1 取 mid，问题就得以解决了。此时：
mid = (left + right + 1) >> 1 = (2 * left + 2) >> 1 = left + 1 = right，可以看出 left 往后了一位。

归根究底还是因为整形数据除 2 会自动进行向下取整的问题，进行 +1 操作后向上取整就可以解决这个问题。

查找等于目标值终止位置图解（取mid向上取整）

（1）

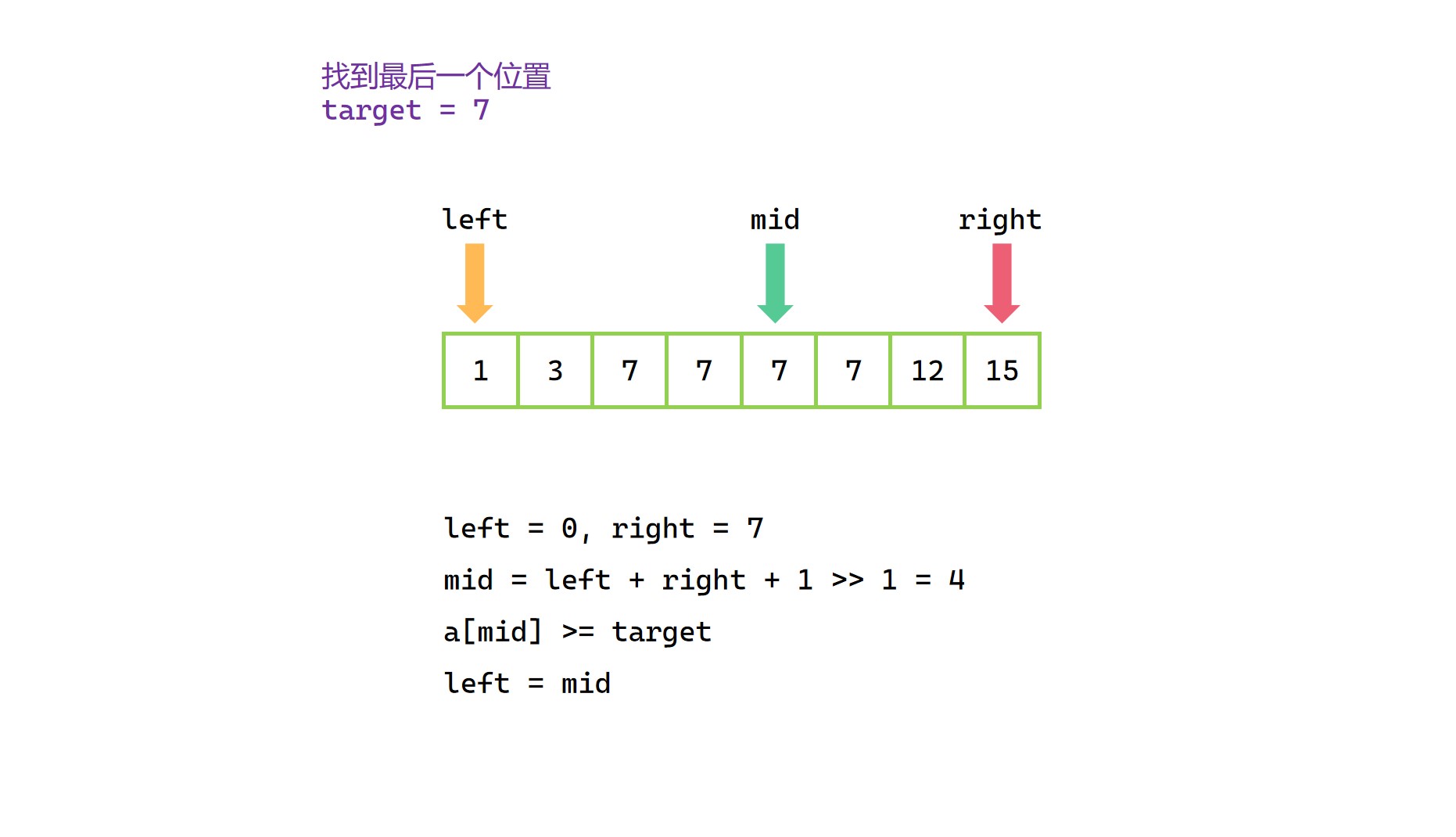
（2）

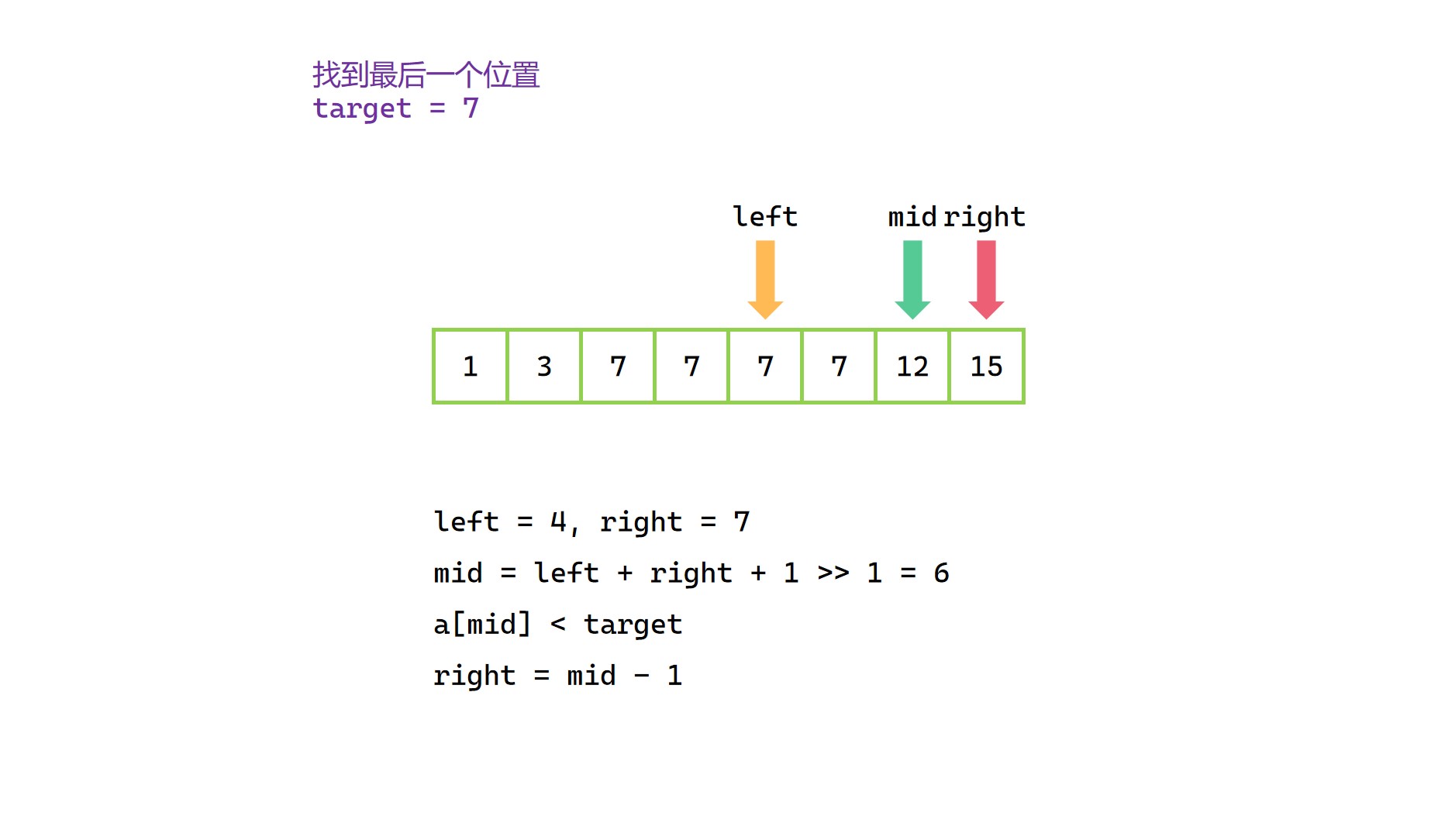
（3）

（4）

查找等于目标值终止位置图解（取mid向下取整）*

（1）

（2）

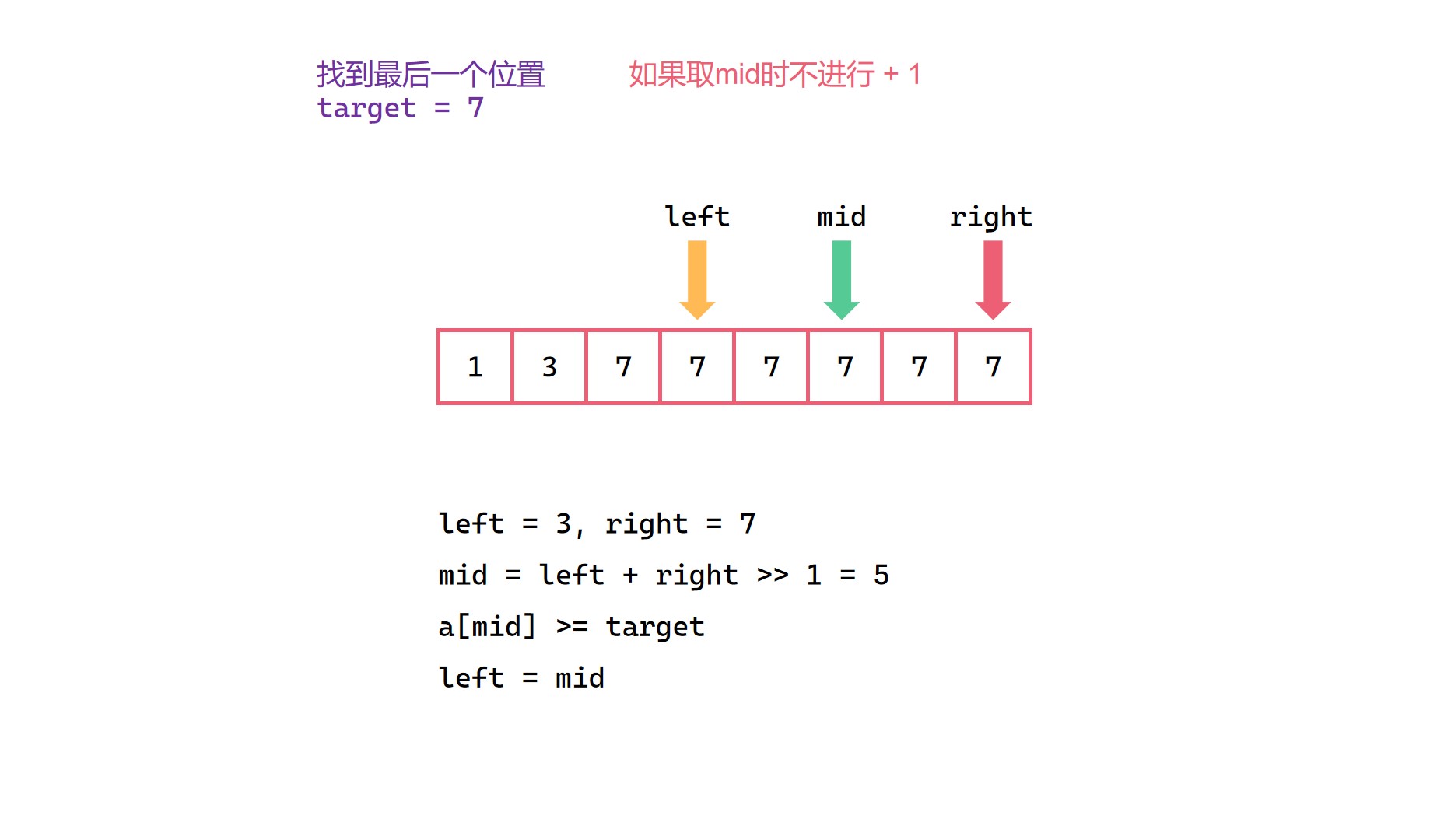
（3）

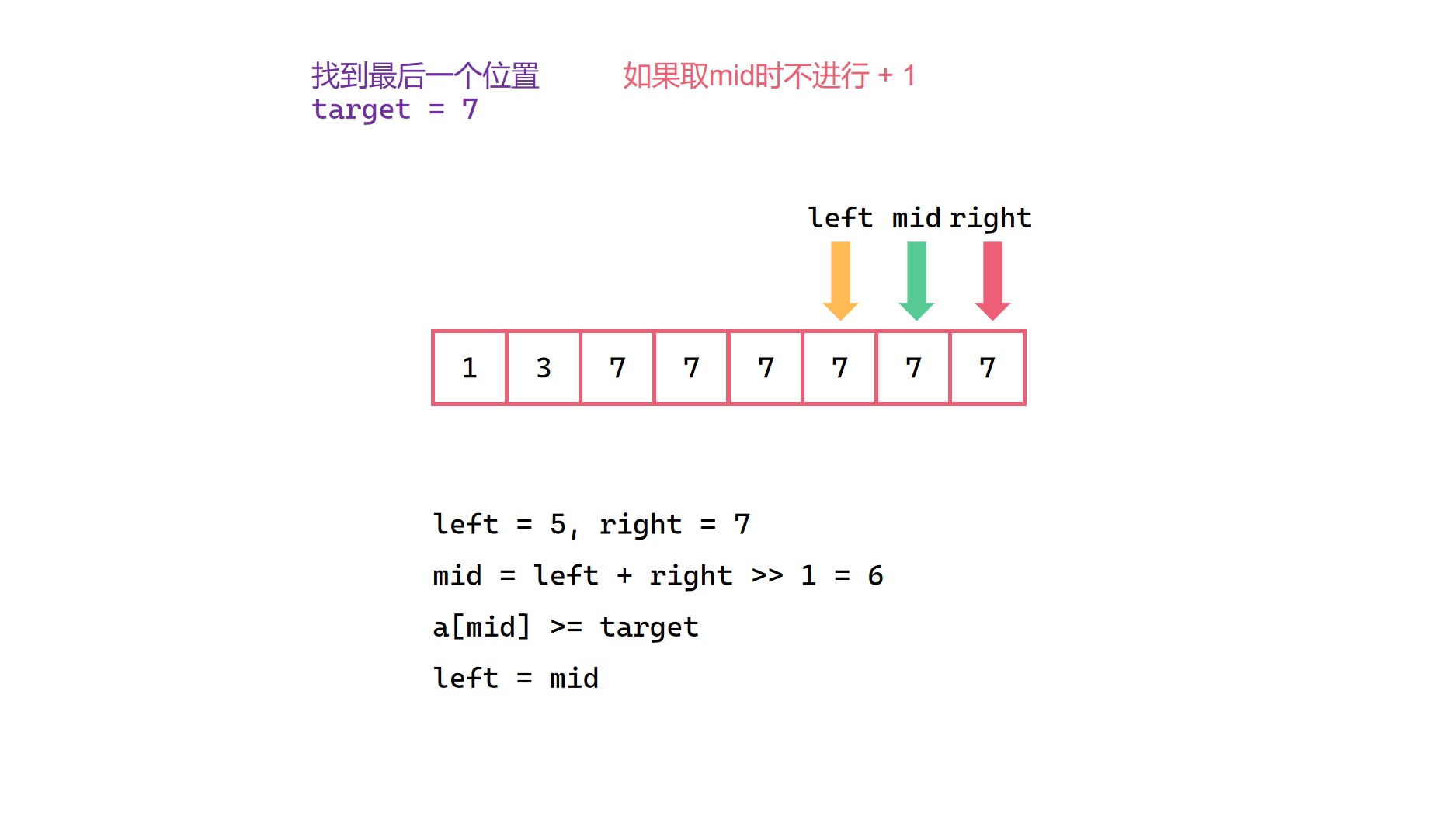
（4）

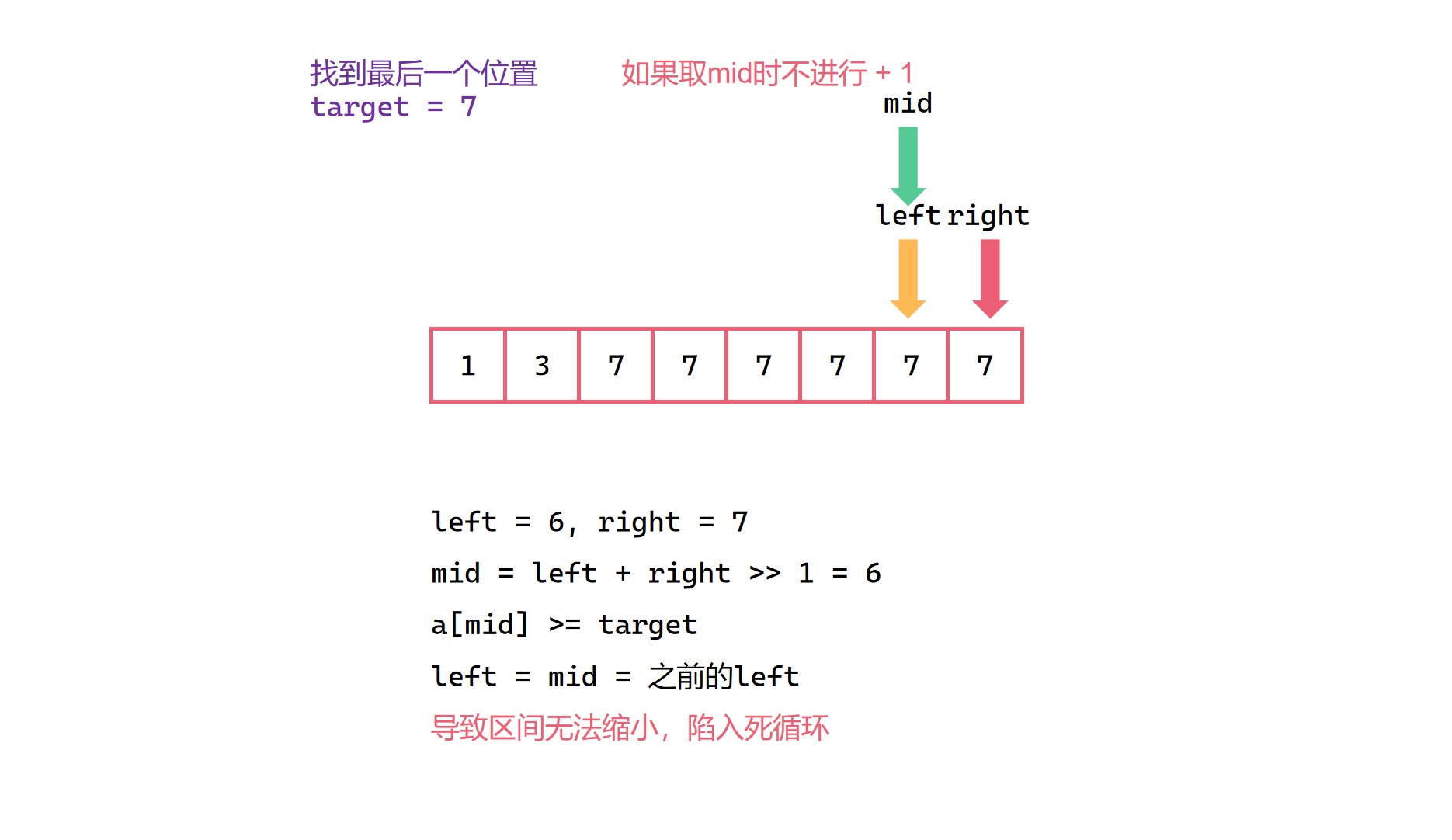
查找等于目标值终止位置代码

int BinarySearchlast(vector<int> &v, int target){
    int left = 0, right = v.size() - 1;
    while(left < right){
        int mid = (left + right + 1) >> 1;
        if(v[mid] > target)
            right = mid - 1;
        else
            left = mid;
    }
    return v[left] == target ? left : -1;
}

---

相关试题及完整程序

相关试题

Acwing 789.数的范围
Leetcode 34.在排序数组中查找元素的第一个和最后一个位置

完整程序

#include<iostream>
#include<vector>
using namespace std;

//二分查找
int BinarySearch(vector<int> &v, int target){
    int left = 0, right = v.size() - 1;
    while(left <= right){
        int mid = (left + right) >> 1;
        if(v[mid] == target)
            return mid;
        if(v[mid] < target)
            left = mid + 1;
        else
            right = mid - 1;
    }
    return -1;
}

//二分查找法递归写法
int BinarySearchRec(vector<int> &a, int left, int right, int target) {
    int mid = (left + right) >> 1;
    if(left <= right){
        if(a[mid] == target)
            return mid;
        if(a[mid] < target)
            return BinarySearchRec(a, mid + 1, right, target);
        else
            return BinarySearchRec(a, left, mid - 1, target);
    }
    return -1;
}

//查找元素起始位置
int BinarySearchfirst(vector<int> &v, int target){
    int left = 0, right = v.size() - 1;
    while(left < right){
        int mid = (left + right) >> 1;
        if(v[mid] < target)
            left = mid + 1;
        else
            right = mid;
    }
    return v[left] == target ? left : -1;
}

//查找元素终止位置
int BinarySearchlast(vector<int> &v, int target){
    int left = 0, right = v.size() - 1;
    while(left < right){
        int mid = (left + right + 1) >> 1;
        if(v[mid] > target)
            right = mid - 1;
        else
            left = mid;
    }
    return v[left] == target ? left : -1;
}

int main(){
    vector<int> v = {7,7,7,7};
    cout<<BinarySearchFirst(v, 7)<<endl;
    cout<<BinarySearchLast(v, 7)<<endl;
    cout<<BinarySearchRec(v, 0, v.size() - 1, 7)<<endl;
    cout<<BinarySearch(v, 7)<<endl;
}