[数据结构] 二叉树的层次遍历

二叉树的层次遍历

层次遍历的思路

二叉树的层次遍历本质上用的是广度优先搜索算法，我们通常使用队列来实现这一过程。

层次遍历的基本步骤

（1）先将二叉树的根节点放入队列中；
（2）取队首节点值，队首节点出队，将节点的左右子树根节点入队；
（3）重复步骤（2），直到队列为空。

层次遍历图解

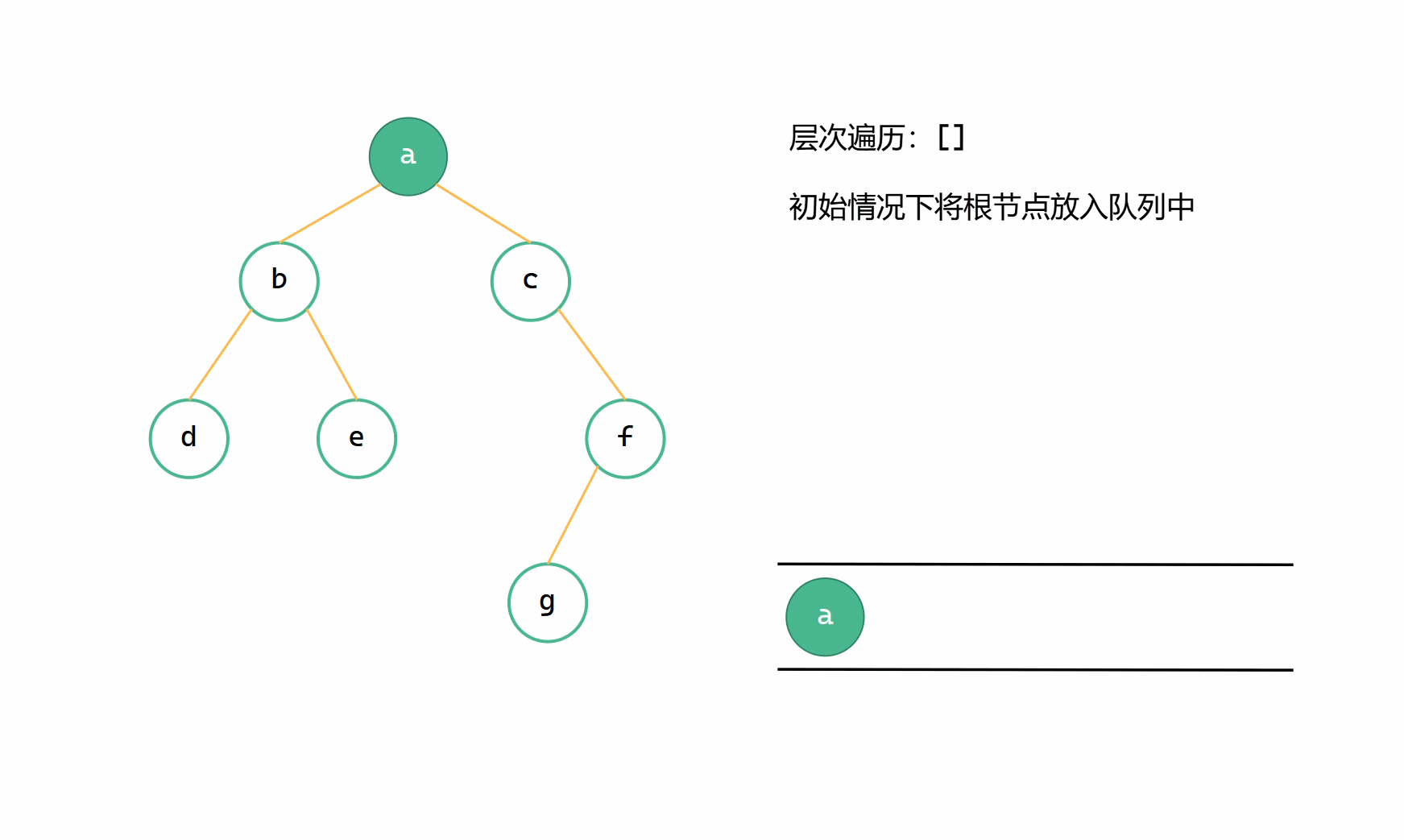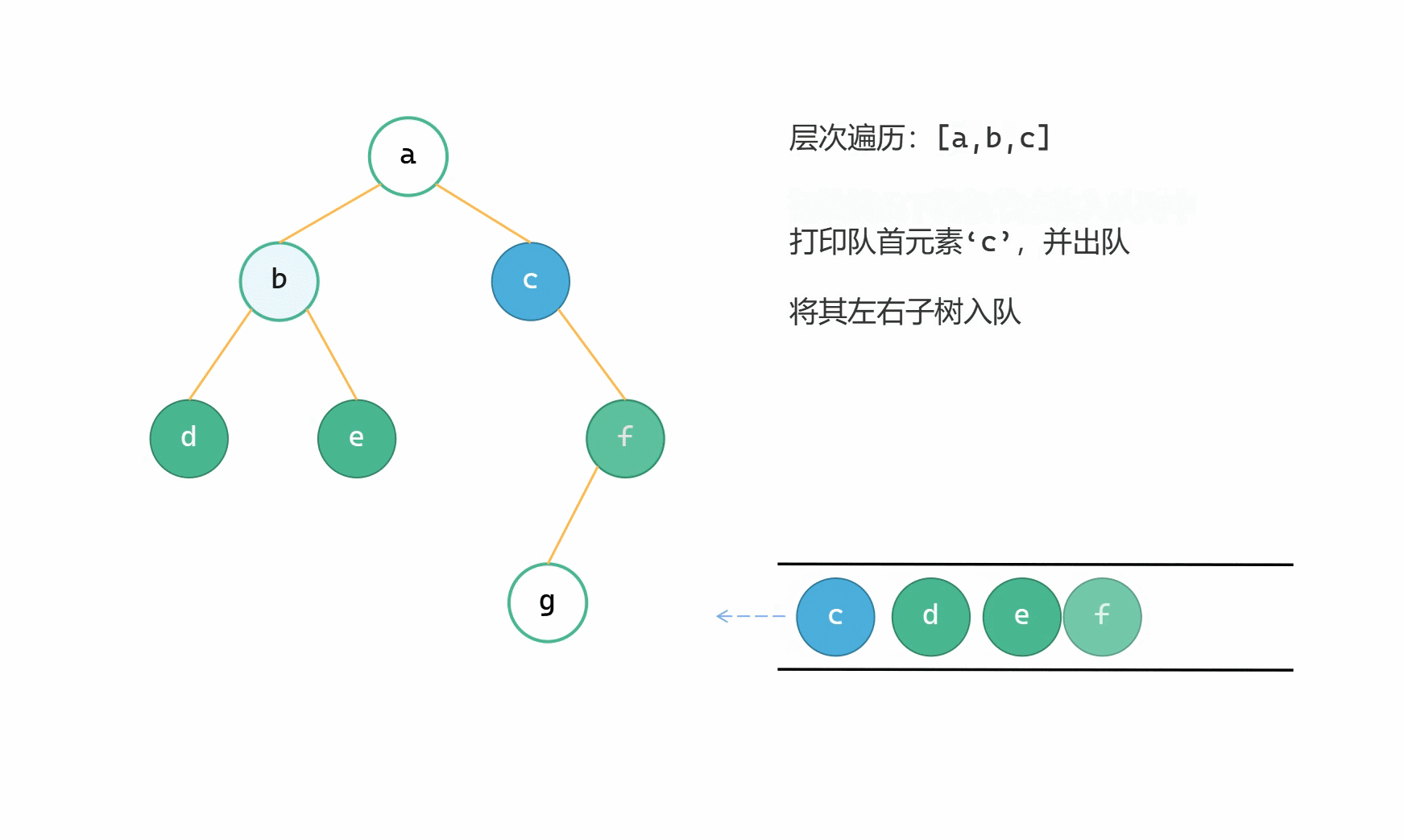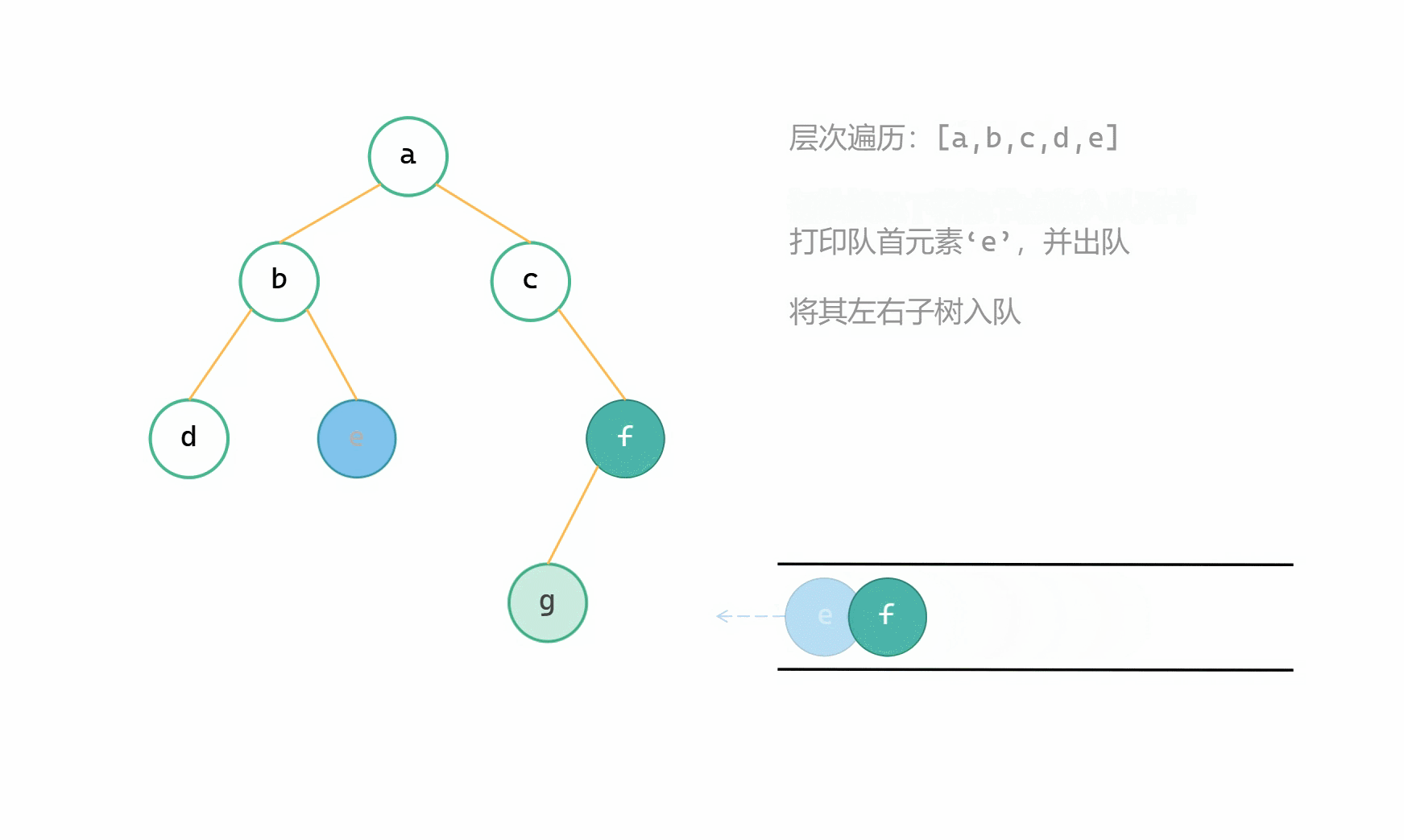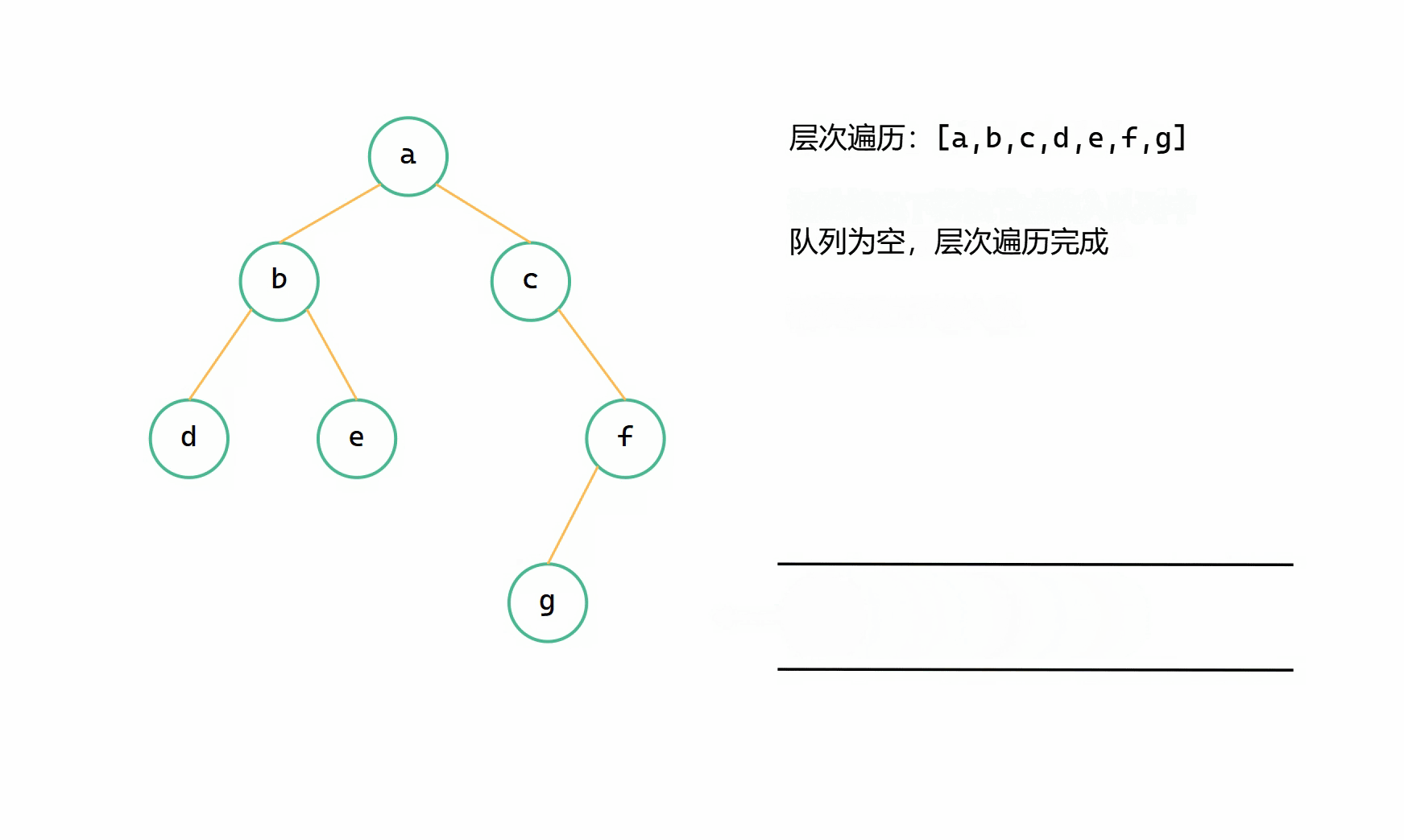
自建队列层次遍历

typedef struct SqQueue{

    BinaryTree data[MAXSIZE];
    int front;
    int rear;

}SqQueue;


SqQueue Q;     //设为全局变量

//队列初始化
void Create_SqQueue(){
    Q.front = Q.rear = 0;
}

//判断队列是否为空
bool IsEmpty(){
    return Q.front == Q.rear;
}

//返回队列当前大小
int QueueSize(){
    return Q.rear - Q.front;
}

//入队 利用队列 层次输入
void Push(BinaryTree T){
    Q.data[++Q.rear] = T;
}

//出队并取队首 利用队列 层次输出
BinaryTree Pop(){
    return Q.data[++Q.front];
}

//层次遍历二叉树  利用自己写的队列
void Show_Level_Order(BinaryTree root){
    BinaryTree t = NULL;
    if(!root) return;

    Push(root);
    while(!IsEmpty()){
        int n = QueueSize();             //取二叉树每层的节点个数
        for(int  i = 0; i < n; i++){
            t = Pop();
            printf("%c ", t->data);

            if(t->leftchild) Push(t->leftchild);    //探索左子树
            if(t->rightchild) Push(t->rightchild);  //探索右子树
        }
        printf("\n");
    }
}

STL queue层次遍历

//利用STL标准库queue层次遍历
void Show_Level_OrderSTL(BinaryTree root){
    BinaryTree t = NULL;
    std::queue<BinaryTree> q;
    if(!root) return;

    q.push(root);
    while(!q.empty()){
        int n = q.size();
        for(int i = 0; i < n; i++){
            t = q.front();
            q.pop();
            printf("%c ", t->data);

            if(t->leftchild) q.push(t->leftchild);
            if(t->rightchild) q.push(t->rightchild);
        }
        printf("\n");
    }
}

---

完整程序

代码

点击查看代码

//#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<queue>
#define MAXSIZE 1000

typedef char Elemtype;
typedef struct BiNode{

    Elemtype data;
    struct BiNode *leftchild;       //左儿子
    struct BiNode *rightchild;      //右儿子

} Node, *BinaryTree;       //BinaryTree结构体指针


typedef struct SqQueue{

	BinaryTree data[MAXSIZE];
	int front;
	int rear;

}SqQueue;


SqQueue Q;     //设为全局变量

//队列初始化
void Create_SqQueue(){
	Q.front = Q.rear = 0;
}

//判断队列是否为空
bool IsEmpty(){
	return Q.front == Q.rear;
}

//返回队列当前大小
int QueueSize(){
    return Q.rear - Q.front;
}

//入队 利用队列 层次输入
void Push(BinaryTree T){
	Q.data[++Q.rear] = T;
}

//出队并取队首 利用队列 层次输出
BinaryTree Pop(){
	return Q.data[++Q.front];
}

//层次遍历二叉树  利用自己写的队列
void Show_Level_Order(BinaryTree root){
	BinaryTree t = NULL;
	if(!root) return;

	Push(root);
	while(!IsEmpty()){
		int n = QueueSize();             //取二叉树每层的节点个数
		for(int  i = 0; i < n; i++){
			t = Pop();
		    printf("%c ", t->data);

		    if(t->leftchild) Push(t->leftchild);    //探索左子树
		    if(t->rightchild) Push(t->rightchild);  //探索右子树
		}
		printf("\n");
	}
}




/*—————————————————————————————————  2  —————————————————————————————————————*/
//利用STL标准库queue层次遍历
void Show_Level_OrderSTL(BinaryTree root){
	BinaryTree t = NULL;
	std::queue<BinaryTree> q;
	if(!root) return;

	q.push(root);
	while(!q.empty()){
		int n = q.size();
		for(int i = 0; i < n; i++){
			t = q.front();
			q.pop();
			printf("%c ", t->data);

			if(t->leftchild) q.push(t->leftchild);
			if(t->rightchild) q.push(t->rightchild);
		}
		printf("\n");
	}
}




//创建二叉树
BinaryTree Create_BinaryTree(){
	Elemtype data;
	BinaryTree T;
	scanf("%c", &data);                       //输入节点数据
	getchar();

	if(data == '#')        //输入#以停止创建子树
		return NULL;
    T = (BinaryTree)malloc(sizeof(Node));
    T->data = data;

    printf("输入 %c 的左儿子数据(#停止): ", data);  //递归创建左子树
    T->leftchild = Create_BinaryTree();
    printf("输入 %c 的右儿子数据(#停止): ", data);  //递归创建右子树
    T->rightchild = Create_BinaryTree();

    return T;
}



int main(){
	BinaryTree T;
	printf("输入二叉树根节点数据: ");
	T = Create_BinaryTree();

	Create_SqQueue();
	printf("\n\n层次遍历二叉树结果: \n");
	Show_Level_Order(T);
	printf("\n");
	Show_Level_OrderSTL(T);
}

运行结果