机器学习笔记
机器学习笔记
第一章 模式识别基本概念
模式识别:根据已有知识的表达,针对待识别模式,判别决策其所属的类别或者预测其对应的回归值,本质上是一种推理过程;从数学角度来看,它可以被看做一种函数映射。
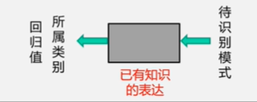
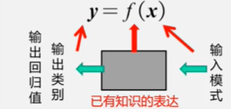
模式识别可以划分为“分类”和“回归”两种形式:
分类:输出量是离散的类别表达,即输出待识别模式所属的类别,分为二类或多类。
回归:输出量是连续的信号表达,输出量是单个或多个维度。
回归是分类的基础,离散的类别值是由回归值做判定决策得到的。
输入空间:原始输入数据x所在的空间,其维度构成输入空间维度。
输出空间:输出的类别/回归值y所在的空间,类别的个数构成回归值的维度。

模型:用于分类,广义上的模型包括特征提取、回归器、判别函数,而狭义上的模型没有判别函数。
分类器由回归器和判别函数组成。
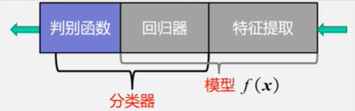
判别函数:使用一些特定的非线性函数来实现,通常记为函数g,通常判别函数固定,所以不把它归于模型的一部分。
sign函数用来进行二类分类,max函数用来进行多类分类。
特征:可以用于区分不同类别模式的、可测量的量,输入数据也可以看作原始特征表达。特征具有辨别能力,提升不同类别之间的识别性能。
鲁棒性:针对不同的观测条件,仍能够有效表达类别之间的差异性。
特征向量:多个特征构成的列向量,可以表达为模长x方向。
模型使用机器学习技术来得到,那么怎样进行机器学习?
(1)需要训练样本

(2)学习模型的参数和结构

其中模型有线性模型和非线性模型

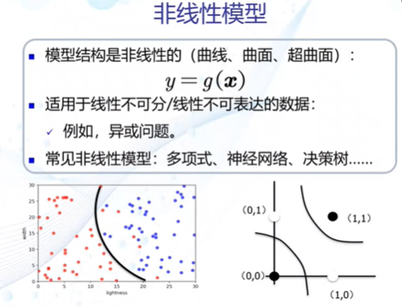
(3)利用训练样本,定义目标函数,使用优化算法来解出一组最优参数作为模式识别的模型

基于学习方式的分类
(1) 监督学习(有导师学习):输入数据中有导师信号,以概率函数、代数函数或人工神经网络为基函数模型,采用迭代计算方法,学习结果为函数。
(2) 无监督学习(无导师学习):输入数据中无导师信号,采用聚类方法,学习结果为类别。典型的无导师学习有发现学习、聚类、竞争学习等。
(3) 强化学习(增强学习):以环境反惯(奖/惩信号)作为输入,以统计和动态规划技术为指导的一种学习方法。
训练集和测试集

训练误差和测试误差

泛化能力:学习算法对新模式的决策能力。

泛化能力低会出现过拟合

提高泛化能力:正确选择模型;正则化。

评估方法:
(1)留出法
直接将数据集划分为两个互斥的集合,2/3-4/5。
划分原则:划分过程尽可能保持数据分布的一致性
方法缺陷:训练集过大,更接近整个数据集,但是由于测试集较小,导致评估结果缺乏稳定性;测试集大了,偏离整个数据集,与根据数据集训练出的模型差距较大,缺乏保真性。
(2)交叉验证法
将数据集划分为k个大小相似的互斥子集,每个子集轮流做测试集,其余做训练集,最终返回这k个训练结果的均值。
优点:更稳定,更具准确定;
缺单:时间复杂的较大
性能指标
精度、召回率


F-score

混淆矩阵

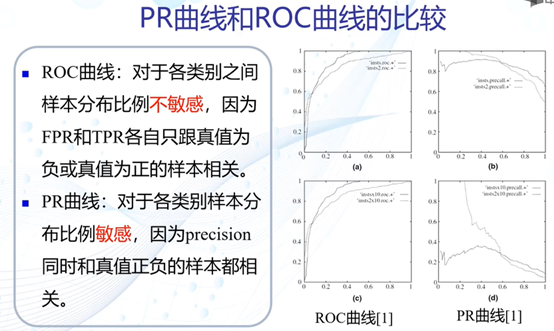
PR曲线

ROC曲线

第二章 基于距离的分类器
MED分类器:把测试样本到每个类之间的距离作为决策模型,将测试样本判定为与其最近的类。
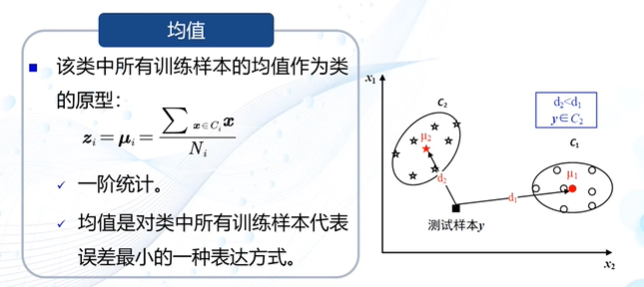
类的原型:
(1)将均值作为类的原型
(2)选取最近邻作为类的原型
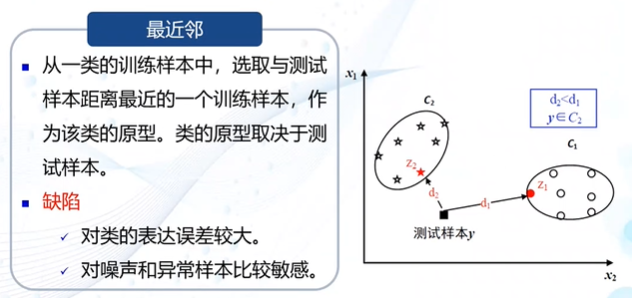
距离度量的三种方式

最小欧氏距离(MED)分类器

特征正交白化的目的

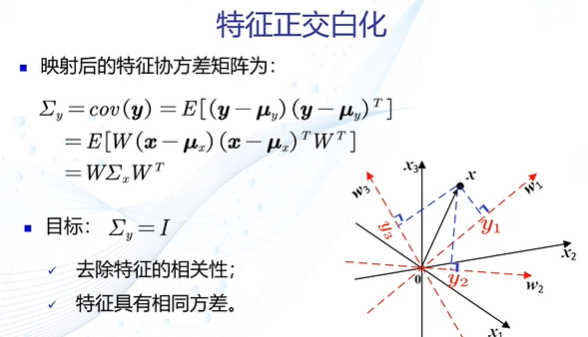
特征转换分为两步:去除特征间的相关性(解耦),再对特征进行尺度变换(白化),使得每维特征的方差相等。

解耦过程



白化过程
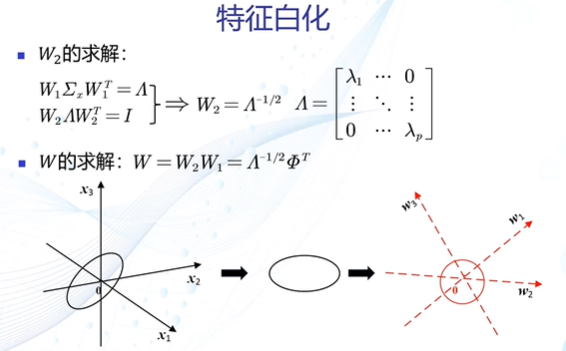

最小类内距离(MICD)分类器:基于马氏距离的分类器

MICD的决策边界

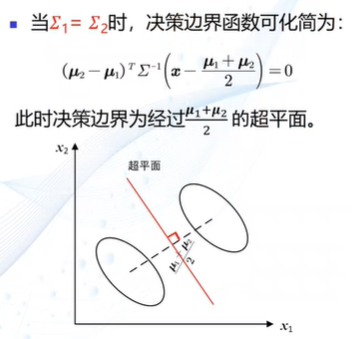

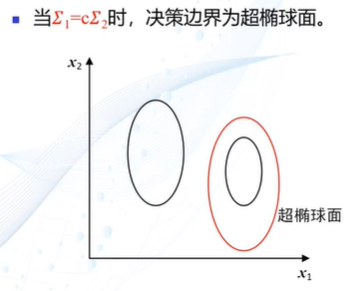
第三章 贝叶斯决策与学习
概率的观点

后验概率:用于分类决策

贝叶斯规则

最大后验概率(MAP)分类器

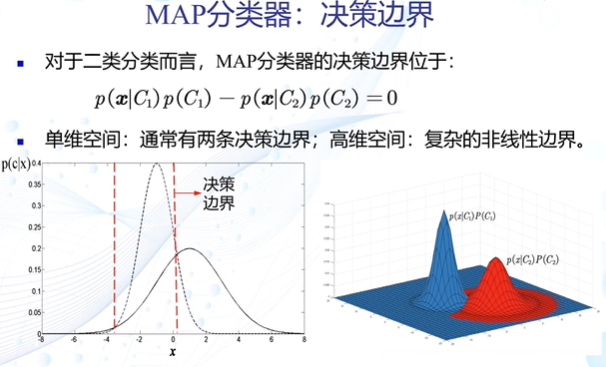
MAP分类器的决策边界
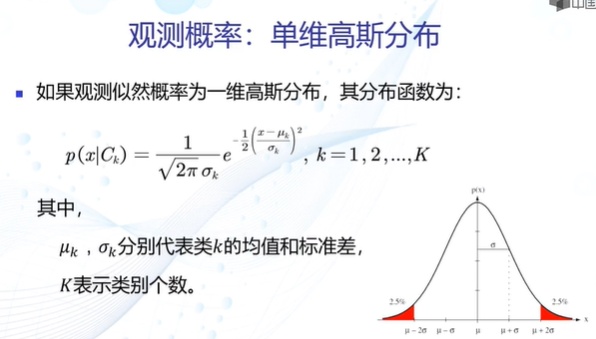
高斯观测概率


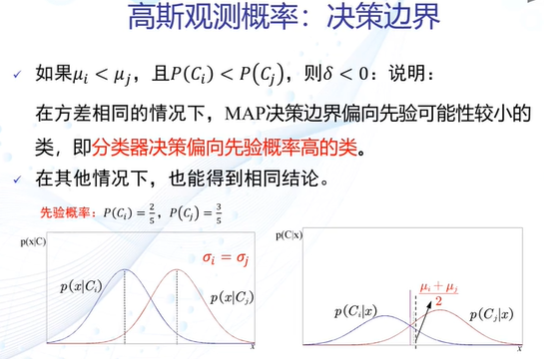
高斯观测概率的决策边界


MAP分类器可以解决MICD分类器存在的问题:
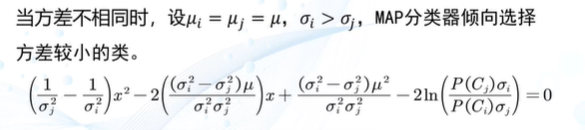
MAP的决策风险

损失的概念

决策风险评估

贝叶斯(Bayes)分类器:MAP+决策风险因素

bayes决策的期望损失

朴素贝叶斯分类器

监督式学习

参数估计方法:
(1)最大似然估计


最大似然估计偏差


(2)贝叶斯估计

无参数估计

K近邻(KNN)估计


KNN分类器

直方图估计
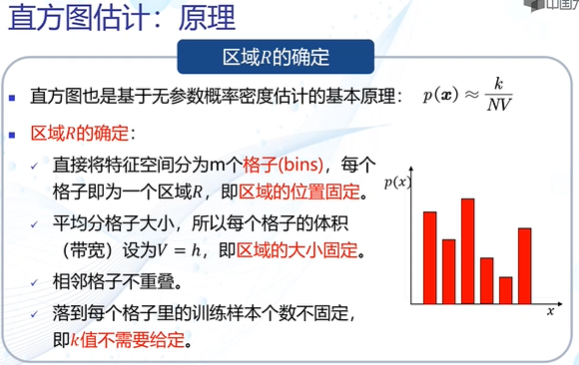

核密度估计




第四章 线性判据与回归
生成模型


判别模型

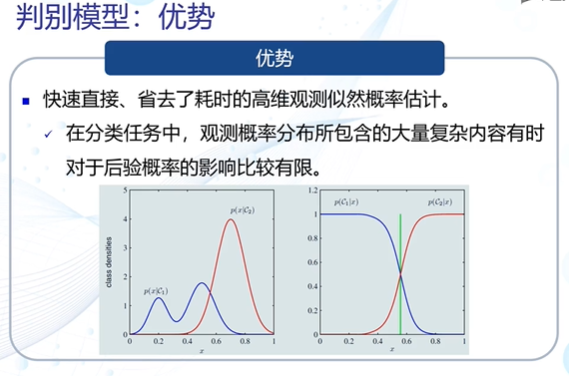
线性判据

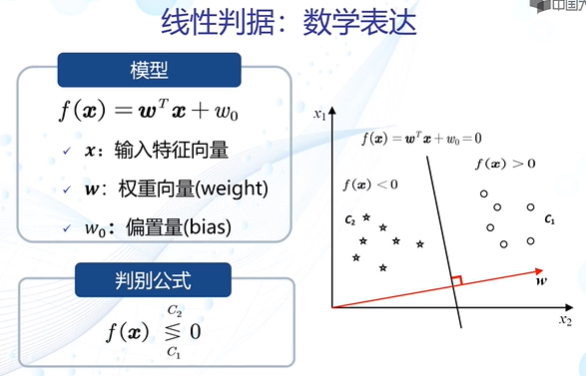

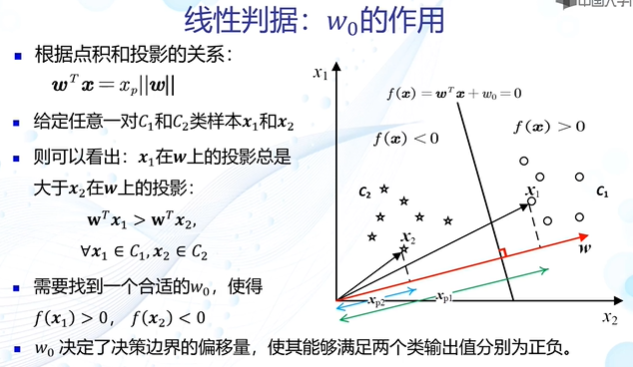

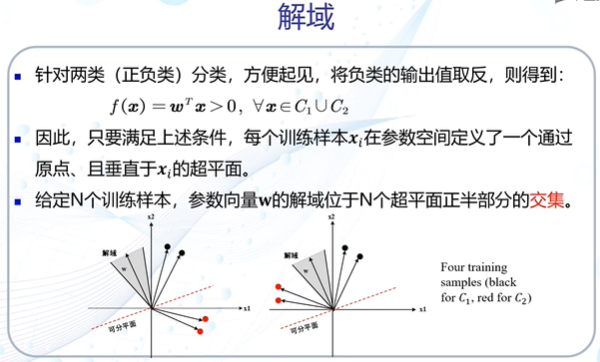
寻求最优解————参数空间&解域

如何找到最优解
(1)设计目标函数

(2)目标函数的求解

(3)加入约束条件

根据目标函数的不同,我们可以设计不同的线性判据算法
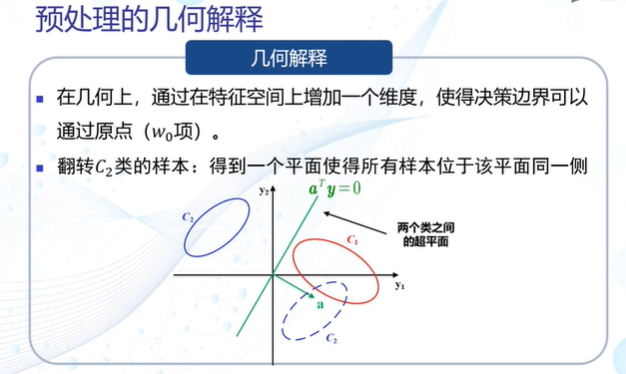
感知机算法:预处理

并行感知机:目标函数

梯度下降法
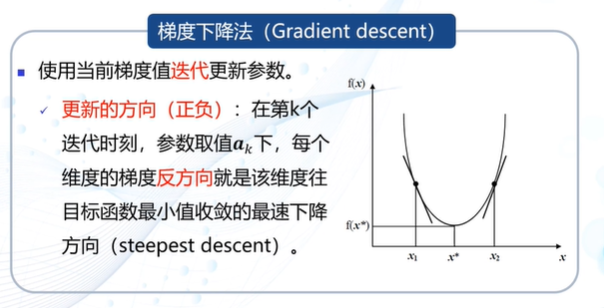
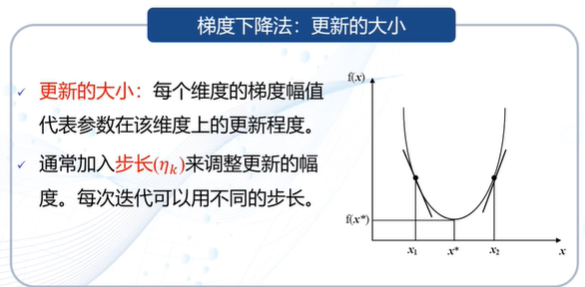
并行感知机:参数更新
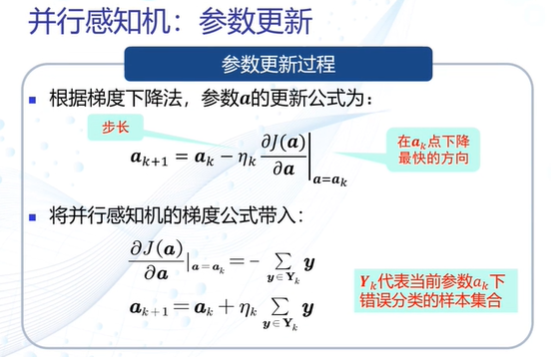
并行感知机:算法流程

如果训练样本是一个一个串行给出的,需要用到串行感知机


收敛性:若训练样本线性可分,则串行、并行感知机理论上收敛于一个解。
加入margin约束,修正边界决策稳定性


Fisher线性判据

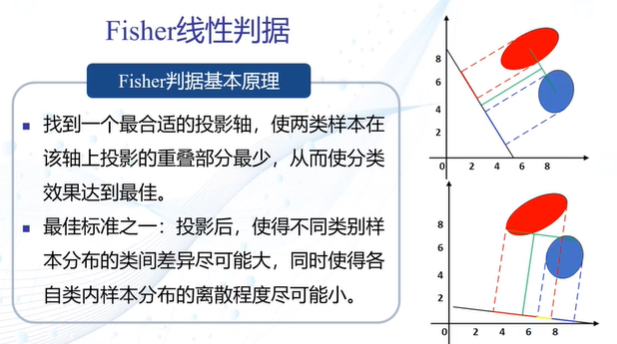
Fisher线性判据:目标函数

支持向量机
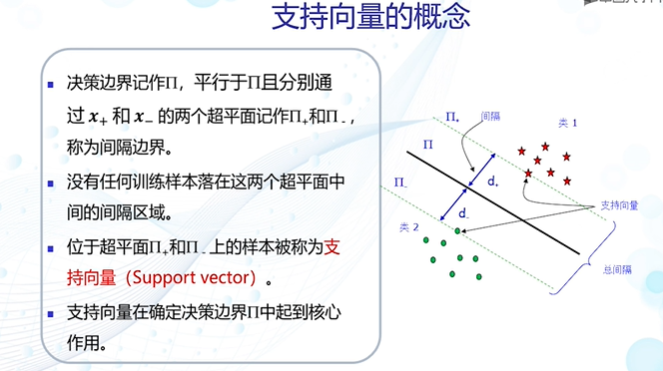
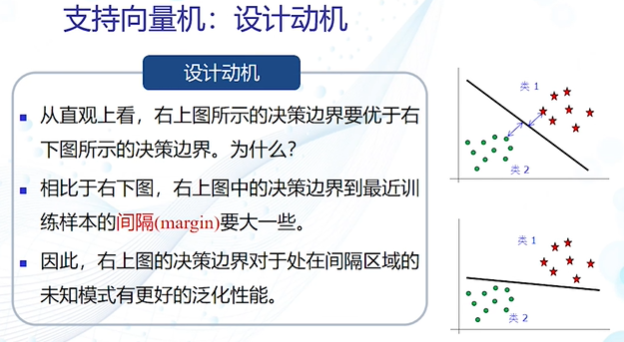


支持向量机的目标函数是条件优化问题,使用拉格朗日乘数法可以得到优化问题的最优解