算法:(二)二叉树
(一)节点结构
- 左节点、右节点、节点值(工程上还有指向父节点的指针)
(二)复杂度
- 不管是递归方法还是非递归方法,遍历整棵树的时间复杂度都是O(N),N为二叉树的节点数,额外空间复杂度为O(L),L为二叉树的层数。
(三)遍历(先中后序遍历都有递归和非递归版本,非递归要另外准备栈)
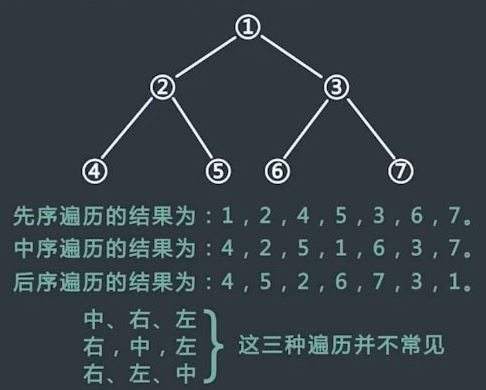
- 先序遍历:中-->左-->右
- 中序遍历:左-->中-->右
- 后序遍历:左-->右-->中
- 按层遍历
- 针对二叉树的宽度优先遍历
- 宽度优先遍历常使用队列结构
- 注意通常题目会对换行有要求
(四)序列化和反序列化
- 二叉树-->字符串(序列化)
- 字符串-->二叉树(反序列化)
- 选择用什么样的遍历方式序列化,就选择用什么样的方式反序列化
- 一棵树的序列化结果是唯一的,唯一的结果生成的二叉树也是唯一的
- 序列化方式:
- 根据先序遍历序列化
- 假设序列化结果为str,初始时str为空字符串
- 先序遍历二叉树时如果遇到空节点,在str末尾加上“#!”
- 如果遇到不为空的节点,假设节点值为3,就在str末尾加上“3!”
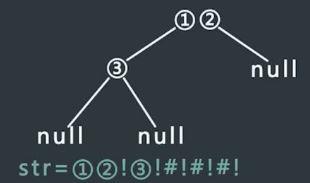
- 根据先序遍历序列化
-
- 根据中序遍历序列化
- 根据后序遍历序列化
- 按层序列化
- 用队列来进行二叉树的按层遍历,即宽度优先遍历
- 除了访问节点的顺序是按层遍历之外,对结果字符串的处理,和之前处理的方式一样。
- 反序列化过程同理
(五)子树
- 二叉树中以任何一个节点为头部的整棵树称作二叉树的子树。
(六)平衡树(AVL树)
- 空树是平衡二叉树
- 若一棵树不为空,并且其中所有的子树都满足各自的左子树与右子树的高度差都不超过1
(七)搜索二叉树
- 每棵子树的头节点的值都比各自左子树上的所有节点值大,比各自右子树上的节点值小
- 按中序遍历得到的序列,一定是从小到大排列的
- 红黑树、平衡搜索二叉树等都是搜索二叉树的不同实现
(八)完全二叉树
- 完全二叉树指除了最后一层之外,其他每一层的节点数都是满的
- 最后一层如果也满了,是一棵满二叉树,也是完全二叉树
- 最后一层如果不满,缺少的节点也全部集中在右边,那也是一棵完全二叉树
(九)满二叉树
- 除了最后一层节点无任何子节点外,剩下每一层上的节点都有两个子节点
- 满二叉树的层数为L,节点数为N,则N=2L-1,L=log2(N+1)
(十)前驱后继节点
- 前驱节点:这个节点在中序遍历序列中的上一个节点
- 后继节点:这个节点在中序遍历序列中的下一个节点
(十一)补充(需要了解)
- 能结合队列、栈、链表、字符串等很多数据结构
- 需要掌握图的基本遍历方式,比如BFS和DFS
- 需要掌握递归函数的使用,并自己设计出递归过程