POJ-3621 Sightseeing Cows 01分数(参数搜索)规划问题-最优比率环
题意:给定N个点,M条单向边,问在图中寻找一条回路,使得该路径上的所有点权和除以边权和最大。
解法:设某点点权为ai, 边权为bi。选择某点的同时就意味着选择了某条边,那么我们把这条单向边划给弧头,因此可以得到表达式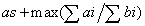 ,s是牛选择的出发点。可以利用01分数规划的一般解法来求解,那就是选择某个比例进行合法性判定,如果这个比例能够达到,则把比例加大,如果不能的话,缩小这个比例,所以也叫做参数搜索,假设这个比例为R后,上式变为
,s是牛选择的出发点。可以利用01分数规划的一般解法来求解,那就是选择某个比例进行合法性判定,如果这个比例能够达到,则把比例加大,如果不能的话,缩小这个比例,所以也叫做参数搜索,假设这个比例为R后,上式变为 是否成立的判定问题。由于一个图中的某条回路小于0可以用spfa进行判定,那么我们就可以得到一个非常接近正确答案的值,只要精度够高,就能够保证得到的答案取两位后能够与等于0的参数R相同。另外此题还有一些不明白的地方,那就是为什么从1开始搜索一定能够找遍所有负环的可能。
是否成立的判定问题。由于一个图中的某条回路小于0可以用spfa进行判定,那么我们就可以得到一个非常接近正确答案的值,只要精度够高,就能够保证得到的答案取两位后能够与等于0的参数R相同。另外此题还有一些不明白的地方,那就是为什么从1开始搜索一定能够找遍所有负环的可能。
代码如下:
#include <cstdlib> #include <cstring> #include <cstdio> #include <iostream> #include <algorithm> using namespace std; int N, M; const double eps = 1e-6; struct Edge { int v, next, ct; }e[5005]; int idx, head[1005]; int fee[1005]; void insert(int a, int b, int c) { e[idx].v = b, e[idx].ct = c; e[idx].next = head[a]; head[a] = idx++; } int sign(double x) { return x < -eps ? -1 : x > eps; } const int MaxN = 1005; int que[1005]; int front, tail; char vis[1005]; int cnt[1005]; double dis[1005]; double cost(int x, int y, double r) { return r * e[y].ct - fee[x]; } bool Ac(double x) { fill(dis, dis+MaxN, 1e9); memset(vis, 0, sizeof (vis)); memset(cnt, 0, sizeof (cnt)); dis[1] = 0, vis[1] = 1; front = tail = 0; que[tail++] = 1; while (front != tail) { int v, u = que[(front++)%MaxN]; double ct; vis[u] = 0; for (int i = head[u]; ~i; i = e[i].next) { v = e[i].v, ct = cost(u, i, x); if (sign(dis[u]+ct-dis[v]) < 0) { dis[v] = dis[u] + ct; if (!vis[v]) { vis[v] = 1, ++cnt[v]; if (cnt[v] >= N) return true; que[(tail++)%MaxN] = v; } } } } return false; } double bsearch(double l, double r) { double mid, ret = 0; while (sign(r-l) >= 0) { mid = (l + r) / 2.0; // 枚举一个参数 if (Ac(mid)) { // 如果找到负环 ret = mid; l = mid + eps; } else { r = mid - eps; } } return ret; } int main() { int a, b, c; while (scanf("%d %d", &N, &M) != EOF) { idx = 0; memset(head, 0xff, sizeof (head)); for (int i = 1; i <= N; ++i) { scanf("%d", &fee[i]); // 读入N各点的费用 } for (int i = 1; i <= M; ++i) { // M条单向边 scanf("%d %d %d", &a, &b, &c); insert(a, b, c); } printf("%.2f\n", bsearch(0, 2000)); } return 0; }




