HDU-4467 Graph 类似于分段函数的思想的解题技巧

题意：给定N个点，M条边，每个点为0或者为1，每条边有一个权值。接下来有Q组操作，要么翻转某个点的标号，要么询问某组边的权值一共为多少，总共有三种类型的边：端点分别为(0, 0), (0, 1), (1, 1)。

解法：这题的一个蛮力的解法就是记录好每一点的标号，然后O(1)的时间修改编号，对于每次查询就遍历所有的边进行询问。这样的话时间复杂度就是O(q*m)了，显然无法接受。

换个好点的，我们首先通过原始数据在输入的时候处理一下，保留好每条边所属的类型。那么在没有点进行修改的话，O(1)时间进行输出。问题就是如果要进行修改的话，一个合理的方式就是修改当前节点所连的边的属性，因为其他于该节点无关的节点是没有影响的。那么修改一个点连接边的复杂度是多少了，好的话可能修改几条或者几十条就够了，但是极端数据是可能达到关于m的一个复杂度。因此这个方法不失为一种好方法，如果能够处理好一些极端数据的话。

处理方法：把图中的点类似分段函数一样的处理，对于度小于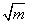的节点我们还是采用前面所说的暴力的办法维护。而对于度大于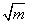的节点就单独拿出来处理。我们维护好度大于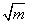节点与之相邻的0的节点和1的节点的边权值总和，这样修改度大点的话根据这两个信息就能够直接得到权值的修改了，比如当前点为0，修改为1，那么(0,0)组合就减少了维护的0的权值，并且把这一部分加到(1, 0)上面去；同理，减少(0, 1)的权值加到(1, 1)上面去。前面谈到维护好相邻的0,1节点边权总和。

这里有一个证明：设度大于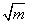的节点数为x，那么有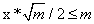，可以得出。

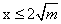因此我们只需要开设一个不大于700*700的矩阵存在这些度大点之间的贡献关系即可。而度小的点则直接通过边的关系来更新度大的点。因此该算法在查询的时候时间复杂度为O(1)，修改的时间复杂度为O(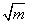)，最终的复杂度为O(q)。

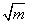代码如下：

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <map>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
int N, M, LIM;
int cl[100005], deg[100005];
LL ans[3]; // 其中ans[0],ans[1],ans[2]表示00、01、11的边的权值总和
LL w[700][700]; // 用来记录特殊点之间的权值关系
int tail; // 特殊点不会超过2*sqrt(M)个
LL fee[700][2]; // 分别记录特殊点与0点相连的边权和，与1点相连的边权和
int sp[100005]; // hash该节点是否为特殊点
map<LL,LL>mp;

struct Edge {
    int v, f, next;
};
Edge e[500005];
int idx, head[100005];

void insert(int a, int b, int f) {
    e[idx].v = b, e[idx].f = f;
    e[idx].next = head[a];
    head[a] = idx++;
}

void init() {
    for (int i = 1; i <= N; ++i) {
        if (deg[i] >= LIM) {
            sp[i] = tail++;
        } // 将度大的点离散化到一个较小的区间 
    }
    map<LL,LL>::iterator it;
    for (it = mp.begin(); it != mp.end(); ++it) {
        int u = it->first / N + 1, v = it->first % N + 1;
        if (~sp[u] && ~sp[v]) { // 如果两个点都是特殊点
            w[sp[u]][sp[v]] += it->second;
            w[sp[v]][sp[u]] += it->second;
            fee[sp[u]][cl[v]] += it->second;
            fee[sp[v]][cl[u]] += it->second;
        } else if (!(~sp[u]) && !(~sp[v])) { // 如果两个点都不是特殊点 
            insert(u, v, it->second); // 有度小的点就需要构边等着以后来暴力了 
            insert(v, u, it->second);
        } else if (~sp[u]) {
            fee[sp[u]][cl[v]] += it->second;
            insert(v, u, it->second);
        } else {
            fee[sp[v]][cl[u]] += it->second;
            insert(u, v, it->second);
        }
    }
}

void change(int x) { // 修改过程 
    if (~sp[x]) { // 如果x是特殊的点
        if (cl[x] == 1) {
            ans[1] -= fee[sp[x]][0], ans[0] += fee[sp[x]][0];
            ans[2] -= fee[sp[x]][1], ans[1] += fee[sp[x]][1];
            for (int i = 0; i < tail; ++i) {
                fee[i][1] -= w[sp[x]][i], fee[i][0] += w[sp[x]][i];
            }
        } else {
            ans[0] -= fee[sp[x]][0], ans[1] += fee[sp[x]][0];
            ans[1] -= fee[sp[x]][1], ans[2] += fee[sp[x]][1];
            for (int i = 0; i < tail; ++i) {
                fee[i][0] -= w[sp[x]][i], fee[i][1] += w[sp[x]][i];
            }
        }
    } else {
        for (int i = head[x]; ~i; i = e[i].next) {
            if (cl[x] == 1) {
                ans[cl[e[i].v]+1] -= e[i].f, ans[cl[e[i].v]] += e[i].f;
                if (~sp[e[i].v]) { // 如果连接的点是特殊点
                    fee[sp[e[i].v]][1] -= e[i].f, fee[sp[e[i].v]][0] += e[i].f;
                }
            } else {
                ans[cl[e[i].v]] -= e[i].f, ans[cl[e[i].v]+1] += e[i].f;
                if (~sp[e[i].v]) {
                    fee[sp[e[i].v]][0] -= e[i].f, fee[sp[e[i].v]][1] += e[i].f;    
                }
            }
        }
    }
    cl[x] ^= 1;
}

int main() {
    int a, b, c, ca = 0;
    while (scanf("%d %d", &N, &M) != EOF) {
        LIM = (int)sqrt(1.0*M); // LIM就是这样的对度数限制的阀值 
        tail = idx = 0;
        mp.clear();
        memset(w, 0, sizeof (w));
        memset(head, 0xff, sizeof (head));
        memset(sp, 0xff, sizeof (sp));
        memset(deg, 0, sizeof (deg));
        memset(ans, 0, sizeof (ans));
        memset(fee, 0, sizeof (fee));
        for (int i = 1; i <= N; ++i) {
            scanf("%d", &cl[i]); // 获取每个节点的原始颜色 
        }
        for (int i = 1; i <= M; ++i) {
            scanf("%d %d %d", &a, &b, &c);
            if (a > b) swap(a, b); // 始终保持a < b，这样才能把所有相同的边合并
            mp[1LL*(a-1)*N+b-1] += c; // 该map用于合并一些边
            ans[cl[a]+cl[b]] += c;
            ++deg[a], ++deg[b];
        }
        init();
        int Q;
        char op[10];
        scanf("%d", &Q);
        printf("Case %d:\n", ++ca);
        while (Q--) {
            scanf("%s", op);
            if (op[0] == 'A') {
                scanf("%d %d", &a, &b);
                // 查询是愉悦的 
                printf("%I64d\n", ans[a+b]);
            } else {
                scanf("%d", &a);
                change(a); // 修改是痛苦的 
            }
        }
    }
    return 0;
}