HDU-4471 Homework 矩阵运算上的优化

题意：给定一个函数定义如下：

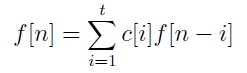
对于q个点满足：

给定f[1]-f[n]的数值，然后存在q个特殊的点，其于前面的关联的项数特殊，系数特殊，当然位置也特殊。现在要求f[n]的值。

解法：如果题目中没有强调q个特殊点的话，那么可以使用矩阵快速幂搞出来。鉴于只有最多100个特殊点，我们可以选择分段进行处理，对每一个空隙进行一次矩阵快速运算，然后对于特殊点单独做一次。这里又有一个地方要特别注意：那就是q个点中有位置大于n的点。

当然仅仅是一般的矩阵快速幂这题的复杂度将达到O(q*log(n)*L^3)，结合多组数据这样会超时，一个优化就是使用一个列向量去依次乘以若干个矩阵，那么每一次相乘的复杂度就变成了L^2，那么最后的复杂度就变成了O(q*log(n)*L^2)。

代码如下：

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

const int MOD = int(1e9)+7;
const int MAXN = 105;
int N, M, Q;

struct Matrix {
    int r, c;
    int a[MAXN][MAXN];
    void init(int rr, int cc) {
        r = rr, c = cc;
        memset(a, 0, sizeof (a));
    }
    void show() {
        for (int i = 1; i <= r; ++i) {
            for (int j = 1; j <= c; ++j) {
                printf("%d ", a[i][j]);
            }
        }
        puts("");
    }
};

Matrix operator * (const Matrix & x, const Matrix & y) {
    Matrix ret;
    ret.init(x.r, y.c);
//    printf("__%d %d %d\n", x.r, x.c, y.r);
    for (int k = 1; k <= x.c; ++k) {
        for (int i = 1; i <= ret.r; ++i) {
            if (!x.a[i][k]) continue;
            for (int j = 1; j <= ret.c; ++j) {
                if (!y.a[k][j]) continue;
                ret.a[i][j] = (1LL*x.a[i][k]*y.a[k][j]+ret.a[i][j])%MOD;
            }
        }
    }
    return ret;
}

Matrix s, pw[35], c, ci[105];
int t, xi[105], ti[105], pos[105];

bool cmp(int a, int b) {
    return xi[a] < xi[b];
}

void getpw() {
    pw[0] = c;
    for (int i = 1; (1 << i) <= N; ++i) {
        pw[i] = pw[i-1] * pw[i-1];
    }
}

void cal(int b) {
    for (int i = 0; i < 31; ++i) {
        if (b & (1 << i)) {
            s = pw[i] * s;
        }
    }
}

void AC() {
    int L = t;
    for (int i = 1; i <= Q; ++i) {
        L = max(L, ti[i]);    
    } // 得到最长的线性关系
    s.r = L, s.c = 1;
    c.r = c.c = L;
    
    for (int i = 2; i <= L; ++i) {
        c.a[i][i-1] = 1;    
    }
    for (int i = 1; i <= Q; ++i) {
        ci[i].r = ci[i].c = L;
        for (int j = 2; j <= L; ++j) {
            ci[i].a[j][j-1] = 1;
        }
    }
    getpw();
    sort(pos+1, pos+1+Q, cmp);
    int last = M;
    for (int i = 1; i <= Q; ++i) {
        int p = pos[i];
        if (xi[p] > N || xi[p] <= last) continue;
        cal(xi[p]-last-1);
        s = ci[p] * s;
        last = xi[p];
    }
    cal(N-last);
    printf("%d\n", s.a[1][1]);
}

int main() {
    int ca = 0;
    while (scanf("%d %d %d", &N, &M, &Q) != EOF) {
        memset(s.a, 0, sizeof (s.a));
        for (int i = M; i >= 1; --i) {
            scanf("%d", &s.a[i][1]);
        }
        scanf("%d", &t);
        memset(c.a, 0, sizeof (c.a));
        for (int i = 1; i <= t; ++i) {
            scanf("%d", &c.a[1][i]);
        }
        for (int i = 1; i <= Q; ++i) {
            pos[i] = i;
            scanf("%d %d", &xi[i], &ti[i]);
            memset(ci[i].a, 0, sizeof (ci[i].a));
            for (int j = 1; j <= ti[i]; ++j) {
                scanf("%d", &ci[i].a[1][j]);
            }
        }
        printf("Case %d: ", ++ca);
        AC();
    }
    return 0;    
}