HDU-4472 Count 递推
题意:有N个节点的图,现在要求构成一棵树(不存在环),且只能够有一个跟节点,每一层的节点数还必须相同。问有多少种不同的方式。
解法:对于N个节点而言,如果第N个节点是N-1个节点任意一种组合情况下的boss的boss,这种事满足情况的,用f[N]表示方案数的话,那么这部分的值就是f[N-1];如果N不属于上面的情况,那么可以认为N个节点的组合下,boss下面就直接分成了一个个支,由于各层节点数要相等,因此每个分支的情况都要一样,所以N-1有多少个大于2的因子就有多少种情况了。
综上: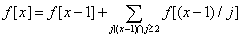 如果把f[x-1]看作一个分支的话,有:
如果把f[x-1]看作一个分支的话,有: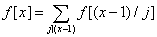
代码如下:
#include <cstdlib> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int MOD = int(1e9)+7; int f[1005]; void pre() { f[1] = f[2] = 1; for (int i = 3; i <= 1000; ++i) { for (int j = 1; j <= i-1; ++j) { if ((i-1) % j == 0) { f[i] += f[(i-1)/j]; f[i] %= MOD; } } } } int main() { pre(); int ca = 0, N; while (scanf("%d", &N) != EOF) { printf("Case %d: %d\n", ++ca, f[N]); } return 0; }





