二叉排序树

概念

    二叉排序树，又称二叉查找树。它或者是一棵空树，或者是具有下列性质的二叉树：
①若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值。
② 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值。
③ 它的左右子树也分别为二叉排序树。

查找、插入和删除操作

package binaryTree;

public class TreeNode {
	int val;
	TreeNode left;
	TreeNode right;

	TreeNode(int val) {
		this.val = val;
	}
}

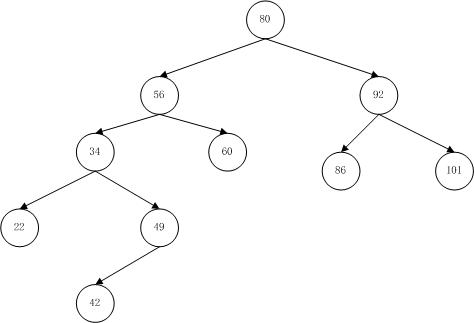
举例

package binaryTree;

import java.util.ArrayList;
import java.util.Scanner;

public class BST {

	// 若查找成功p指向该数据元素结点，否则p指向查找路径上访问的最后一个结点;
	private static TreeNode p;

	/**
	 * 查找操作
	 * 
	 * 思路：根据二叉排序树的性质，分左右子树进行递归查找；
	 * 
	 * @param root
	 *            当前结点；
	 * @param f
	 *            当前节点的父结点；
	 * @param p
	 * 
	 * @param key
	 *            关键值
	 */
	private static boolean BST_search(TreeNode root, TreeNode f, int key) {
		if (root == null) {
			p = f;
			return false;
		} else if (key == root.val) {
			p = root;
			return true;
		} else if (key > root.val) {
			return BST_search(root.right, root, key);
		} else {
			return BST_search(root.left, root, key);
		}
	}

	/**
	 * 插入操作；
	 * 
	 * 思路：先查找原二叉树是否存在，不存在插入，存在则不插入；
	 * 
	 * @param key
	 *            关键值
	 */
	private static boolean BST_insert(TreeNode root, int key) {

		p = null;
		if (!BST_search(root, null, key)) { // 不存在，则插入，p是查找的最后一个节点；
			TreeNode node = new TreeNode(key);
			if (p == null) { // 根节点；
				root = node;
			} else if (p.val < key) { // node作为右结点；
				p.right = node;
			} else { // 作为左节点；
				p.left = node;
			}
			return true;
		} else { // 已经存在；
			return false;
		}
	}

	private static void clear() {
		p = null;
	}

	/**
	 * 删除操作；
	 * 分情况：1、待删除的点为叶子结点（直接删除）；2、只有左或者右分支（子承父业）；3、左右分支都存在（找中序遍历待删结点的前驱或者后继结点代替）；
	 * 
	 * @param root
	 *            当前结点；
	 * @param key
	 *            关键字；
	 * @return
	 */
	private static boolean BST_delete(TreeNode root, int key) {
		if (root == null) { // 树为空，则不存在关键字为key的值；
			return false;
		} else {
			if (key == root.val) { // 找到；
				return deleteNode(root);

			} else if (root.val > key) { // 到左子树中去查找；
				return BST_delete(root.left, key);
			} else {// 到右子树中去查找；
				return BST_delete(root.right, key);
			}
		}
	}

	/**
	 * 删除结点；
	 * 
	 * @param root
	 * @return
	 */
	private static boolean deleteNode(TreeNode root) {
		if (root.left == null && root.right == null) { // 叶子结点；
			root = null;

		} else if (root.left == null) {// 左子树为空，则右子树的根结点代替；
			root = root.right;

		} else if (root.right == null) { // 右子树为空，则左子树的根结点代替；
			root = root.left;

		} else { // 左右子树都存在；
			// 首先找到该结点的中序遍历的前驱结点，即左子树的最右端的结点；
			TreeNode f = root;
			TreeNode p = f.left;// 左子树的根结点；
			while (p.right != null) {
				f = p;
				p = p.right;
			}
			// 找到最终的的前驱f;
			root.val = p.val;
			if (f == root) { // 重新连接q的左子树；
				f.left = p.left;
			} else { // 重新连接q的右子树；
				f.right = p.left;
			}
			p = null;

		}
		return true;
	}

	/**
	 * 中序遍历
	 * 
	 * @param root
	 */
	private static void inOrderTraverse(TreeNode root, ArrayList<Integer> list) {
		if (root == null) {
			return;
		}

		inOrderTraverse(root.left, list);
		list.add(root.val);
		inOrderTraverse(root.right, list);

	}

	public static void main(String[] args) {

		TreeNode root = null;
		ArrayList<Integer> list = new ArrayList<Integer>();
		int[] arr = { 80, 56, 92, 34, 60, 86, 101, 22, 49, 58, 72, 42 };

		for (int i : arr) {
			if (root == null) {
				root = new TreeNode(i);// 根节点显示给出单独；;
			} else {
				BST_insert(root, i);
			}
		}

		// 原二叉排序树；
		inOrderTraverse(root, list);
		System.out.println("删除前："+list);

		// 清空p；
		clear();

		// 删除56这个结点；
		BST_delete(root, 56);

		// 清空List;
		list.clear();
		// 删除后结构没有改变；
		inOrderTraverse(root, list);
		System.out.println("删除结点56后："+list);

	}
}

运行结果：