B-树 C++模板类封装（有图有真相）

定义：

一棵m阶B-树是拥有以下性质的多路查找树：

1、非叶子结点的根结点至少拥有两棵子树；

2、每一个非根且非叶子的结点含有k－1个关键字以及k个子树，其中⌈m/2⌉≤k≤m；

3、每一个叶子结点都具有k－1个关键字，其中⌈m/2⌉≤k≤m；

4、key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间

5、所有的叶子结点都在同一层。

ps： ⌈m/2⌉是向上取整

建立B-树的节点：

template<class K,int M=3>
struct BTreeNode
{
	K _key[M];	//关键字 (有效关键字个数为M-1)
	BTreeNode<K, M>* _sub[M + 1];	//链接子树的指针数组
	size_t _size;		//节点中关键字的个数
	BTreeNode<K, M>* _parent;	//指向父节点的指针

	BTreeNode()
		:_size(0)
		, _parent(NULL)
	{
		for (size_t i = 0; i < M + 1; i++)
		{
			_sub[i] = NULL;
		}
	}
};

插入数据key：

 M阶B树--M=3：

用例 {53, 75, 139, 49, 145, 36, 101};

 

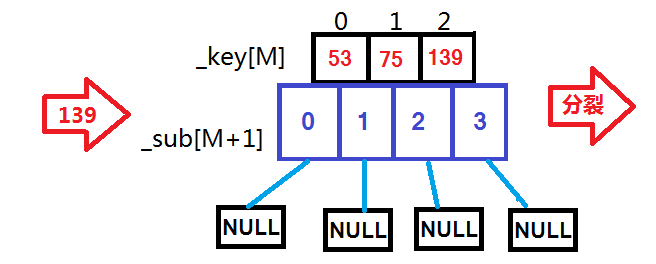
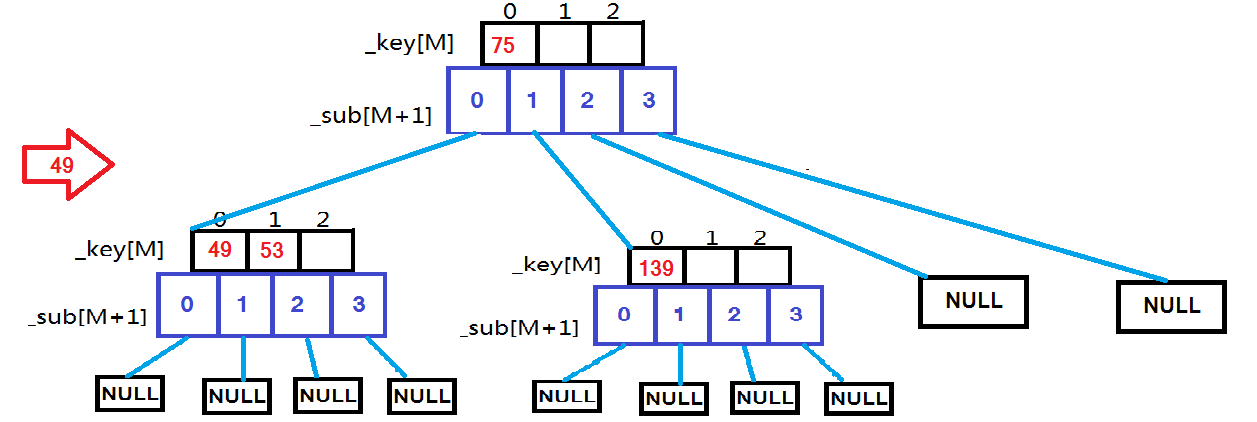
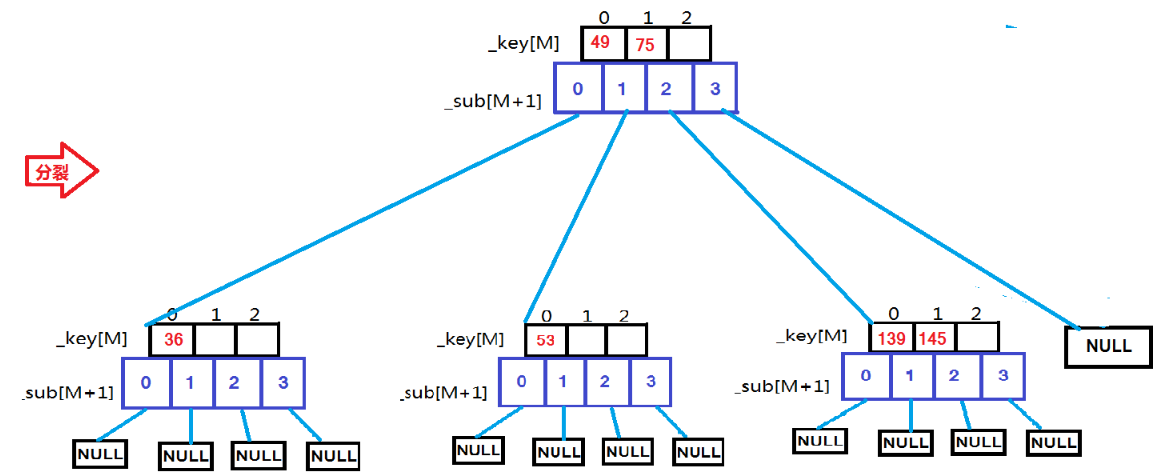
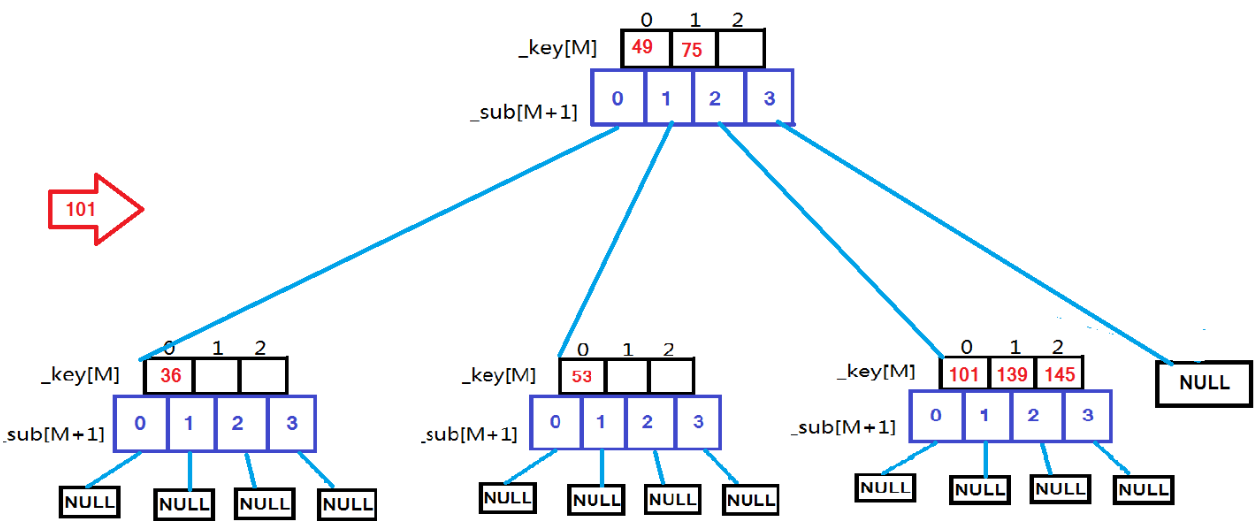
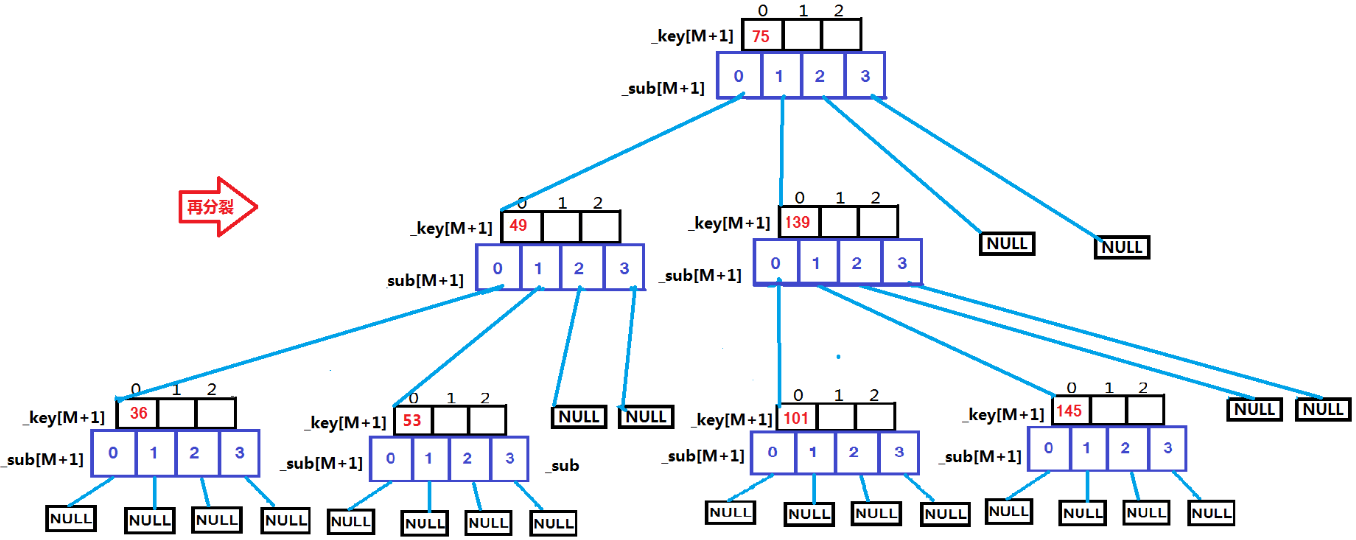
根据上面这些图，依次插入这些数据时的变化一目了然。现在就来看代码：

在插入一个数据前，我们首先要找到你要插入的位置，这里实现一个find函数寻找插入点，辅助插入数据key；

但是这里find函数的返回值该如何处理？bool或int都不行，这两个都不能满足我们的要求。BTreeNode类型也不太合适，找到key就返回该节点无可厚非；但是如果你查找的时候已经遍历到NULL了，说明没有找到数据key，这时候难道返回NULL吗？显然不合适，要插入的位置不能是NULL，这时候应该返回的是当前NULL的父亲结点，也就是我要插入数据的位置了。

那么找到就返回该节点以及该数据所在的关键字数组的下标，未找到就返回-1及父节点，这里我们可以将将它们封装起来，如下：

template<class K,class V>
struct Pair
{
	K _first;
	V _second;
	
	Pair(const K &k = K(), const V& v = V())
		:_first(k)
		, _second(v)
	{}
};

返回值类型确定好的，其它的就好办了：

查找函数思想:

遍历关键字数组_key[]，如果key比它小就 ++i 并继续往后遍历
1.如果key=_key[i]则停止遍历，返回该结构体节点
2.如果key比它大则停止遍历，此时的子树_sub[i]指向的关键字数组的所有数据都是介于_key[i-1]和_key[i]之间的数据，我们要找的key或许就在其中
3.如果跳出循环则未找到该数据cur=NULL，返回cur的父节点；这时候若是插入key，就插入到parent指向的关键字数组中

        //递归查找key
	Pair<BTreeNode<K, M>*, int> Find(const K& key)
	{
		BTreeNode<K, M>* parent=NULL;
		BTreeNode<K, M>* cur=_root;
		
		while (cur!=NULL)
		{
			size_t i = 0;
			while (i < cur->_size&&cur->_key[i] < key)
				++i;
			if (cur->_key[i] == key)
				return Pair<BTreeNode<K, M>*, int>(cur, i);	
			// key<_key[i] 则走向与key[i]下标相同的子树
			parent = cur;
			cur = cur->_sub[i];
		}
		return Pair<BTreeNode<K, M>*, int>(parent, -1);
	}

找到位置后，就可以插入该数据key了

分情况：

1.B-树为NULL

2.B-树中已经存在key

3.B-树中不存在key，先把key以插入排序的方式插入到关键字数组中，判断该关键字数组是否已满，满了就要进行分裂。注意，这里的分裂有时可能不止一次！

//插入数据
	bool Insert(K& key)
	{
		// 1.B-树为空
		if (NULL == _root)
		{
			_root = new BTreeNode<K, M>;
			_root->_key[0] = key;
			++_root->_size;
			return true;
		}

		Pair<BTreeNode<K, M>*, int> ret = Find(key);
		// 2.该数据已经存在
		if (ret._second != -1)	
			return false;

		// 3.插入数据到关键字数组
		BTreeNode<K, M>* cur = ret._first;
		BTreeNode<K, M>* sub = NULL;
		while (1)
		{
			int i = 0;
			for ( i = cur->_size - 1; i >= 0; )
			{ // 把大数往后挪，对应子树也要进行挪动
				if (cur->_key[i] > key)
				{
					cur->_key[i + 1] = cur->_key[i];
					cur->_sub[i + 2] = cur->_sub[i + 1]; 
					i--;
				}
				else
				{
					break;
				}
			}
			cur->_key[i + 1] = key;
			cur->_sub[i + 2] = sub;
			if (sub!=NULL)
				cur->_sub[i+2]->_parent = cur;
			cur->_size++;

			//关键字数组未满，插入成功
			if (cur->_size < M)
				return true;

			//关键字数组已满，需要进行分裂
			int mid = M / 2;
			BTreeNode<K, M>* tmp = new BTreeNode<K, M>;
			int index = 0;
			size_t k;

			for ( k = mid + 1; k < cur->_size; k++)
			{
				tmp->_key[index] = cur->_key[k];
				if (cur->_sub[k] != NULL)
				{
					tmp->_sub[index] = cur->_sub[k];
					cur->_sub[k] = NULL;
					tmp->_sub[index]->_parent = tmp;
				}
				tmp->_size++;
				cur->_size--;
				index++;
			}
			if (cur->_sub[k] != NULL)
			{
				tmp->_sub[index] = cur->_sub[k];
				cur->_sub[k] = NULL;
				tmp->_sub[index]->_parent = tmp;
			}
			//父节点为空时的链接
			if (cur->_parent == NULL)
			{
				_root = new BTreeNode<K, M>;
				_root->_key[0] = cur->_key[mid];
				cur->_size--;
				_root->_sub[0] = cur;
				_root->_sub[1] = tmp;
				_root->_size++;
				
				//链接
				tmp->_parent = _root;
				cur->_parent = _root;
				return true;
			}
			//父节点不为空时的链接
			key = cur->_key[mid];
			cur->_size--;
			cur = cur->_parent;
			sub = tmp;
		}
	}

　　要看完整代码，可以去我的github查看代码：https://github.com/Lynn-zhang/BTree