Java数据结构之链表的原理及LinkedList的部分源码剖析
一、为什么要学习数据结构?
- 做为一名程序员,不管你是用什么编程语言,数据结构是取底层的东西。就相当于盖楼的地基一样,地基做不好,上边再好也没有用。
- 在高级语言中,一般会对这些基础的数据结构进行封装,我们学要学习这些基础的东西吗?
当然是的,只有知道这些基础的东西,我们才能更好地使用语言封装好的api。举个最简单的例子,在Java中,List的实现类有ArrayList,LinkedList,Vector,你知道在什么情况下用哪个效率最高吗?只有知道其底层源才能更好地利用。 - 如何学习数据结构?
可以看书,看视频,看博客...但是最重要的一点,一定要自己用手去敲,比如自己去写一个链表,自己去模拟一个栈,一个队列等。可能你写的没有在语言中封装的那么用好,但是你一定会收获颇丰的。 - 视频书籍哪里找?
微信关注公众号“小鱼与Java”,后台回复数据结构,有我已经整理好的资料。
二、什么是数据和数据结构?
数据就是一些或某部分有关系的内容的组合。
数据结构是数据的存储方式。从不同的角度来讨论,分类如下:
| 按逻辑结构分 | 按物理结构分 |
|---|---|
| 线性结构 | 顺序存储结构 |
| 集合结构 | 链式存储结构 |
| 树形结构 | - |
| 图形结构 | - |
- 逻辑结构,即按照人们的思维逻辑对其分类。
- 物理结构就是数据在磁盘上的存储方式,可以是一整块存储区域,也可以是不同的存储块(但是它们之前有关系,所以就划分为一组数据)。
二、物理结构分法的分类
顺序存储
就是在磁盘上连续存储的,在Java中就是数组,它从第一个索引开始,所有的数据都是紧跟其后的。
链式存储
这些数据(称为数据元素,是不可再分隔的)在磁盘上是分开存储的,只是因为它们之间有一些关系,所以我们就将其联系到了一起,组成了一种数据结构————链表。
代码实现
对于顺序存储的来说,在Java中就是数组,所以不做代码实现。
对于链式存储,就是在其中任何一个元素,除了存储它本身的数据外,还存储另一个或多个数据元素的存储位置。主要分类有下:
单向链表:
就是在这个元素中,除了存储它自身的数据还存储了它的下一个数据

class LinkedNode<T> {
private T data;
private LinkedNode<T> next;
public LinkedNode(T data) {
this.data = data;
//在构建这个时,我们就让它的下一个指针为null
next = null;
}
}
接下来写一个管理它的类,我们写一个add(T t)方法,就是插入到最后
public class MyLinked<T> {
/**
* 用一个头指针来表示这个链表的头
*/
private LinkedNode<T> first;
public MyLinked() {
}
/**
* 提供一个有参构造方法
*
* @param t
*/
public MyLinked(T t) {
this.first = new LinkedNode<>(t);
first.next=null;
}
/**
* 往链表中添加元素,默认是添加到最后的
*
* @param t
*/
public void add(T t) {
if (first == null) {
first = new LinkedNode<>(t);
} else {
LinkedNode herd = first;
while (herd.next != null) {
herd = herd.next;
}
//当从这个循环中出来的时候,这个herd.next就是null,也就是说这个herd就是这个链表的最后一个元素
herd.next = new LinkedNode(t);
}
}
}
我们写的这个add方法,是要遍历整个链表来做此操作。
以上就是最简单的一个链表类了,我们使用了泛型为了让其更加通用。
双向链表
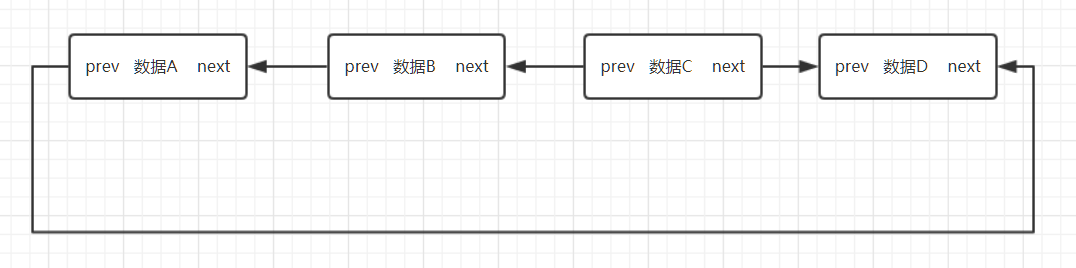
双向链表就是在这个链表中存储了自身的数据,还存储了它的前一个和后一个数据的地址。
class LinkedNode<T> {
private T data;
private LinkedNode<T> prev;
private LinkedNode<T> next;
public LinkedNode(T data) {
this.data = data;
this.prev = null;
this.next = null;
}
}
循环链表表
- 它也分为单向循环链表和双向循环链表
- 在单向链表中,最后一个元素的next不是null,而是指向第一个元素
- 在双向链表中它的第一个元素的prev是最后一个元素,最后一个元素的next是第一个元素。
- 因为它是双向循环的,所以在效率上要比单向的下快一些。
比如,这个链表的长度是50,我们要找第48个元素。如果是单身的话,它只能从0->1->2.....->48,这样要遍历前48个元素;如果是双向的话,我们只需要50->49->48,三次就够了。 - Java中的LinkedList就是底层就是双向循环链表。我们来瞅一下它的源码:
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
我们主要看一下,它的最基本的add方法,来体验一个它的魅力
- 它有add(E e)和add(int index, E e)两个方法
add(E e)就是添加到链表的最后,最终调用的方法如下:
void linkLast(E e) {
//将当前的最后一个节点保存下来
final Node<E> l = last;
//构造一个新的节点对象
final Node<E> newNode = new Node<>(l, e, null);
//将这个链表的last指向这个新元素
last = newNode;
if (l == null){
//这个条件就是说,此时链表为空。因为l是在添加之前的last,如果这个链表为空,last肯定是空的
first = newNode;
}else{
l.next = newNode;
}
size++;//当前的链表大小++
modCount++;//这个是用来记录这个链表的操作次数,对这个链表进行的任何操作,这个都会++
}
上边的构造方法
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
这个插入到时最后的链表并没有去遍历一个整个链表,而是将last.next指向了这个新的节点
add(int index, E e)插入到指定位置
这个最重要的就是利用循环列表来找到这个index是在前半边还是后半边,主要寻找的代码如下:
Node<E> node(int index) {
if (index < (size >> 1)) {
//上边的>>就是取半,除以2
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
可以看到,它判断了所在的部分进行了不同的遍历方式,就是对二分法的一次简利用
当然,它内部还写了迭代等其他的方法,感兴趣的可以自己看一下。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号