[DMY]2024 NOIP 模拟赛 Day 1

前言

今天的四道题感觉做着挺顺的。

但是挂了 100pts。

赛时

看一下 T1，发现是一道一眼看不出来解法的题。

想了半天发现可以按照数字从小到大的顺序依次构造，然后基于这个可以得出一个 $n^2$ 的 DP 状态，设 $d{p}_{i,j}$ 表示第一个人拿了 $i$ 个数字，第二个人拿了 $j$ 个数字时的方案数。

然后根据添加顺序和当前结构可以得出 $dp$ 的转移方式，然后就可以得到一个 $\mathcal{O}(n^2)$ 复杂度的解法。

蹲了个号子回来以后根据这个状态转移方程的两种转移情况相似而不相关可以想到对于每一个 $0$ 和 $1$ 的连续子序列能分开考虑。

然后结合自己的程序打表，推了一大会，我发现答案是每段的卡特兰数之和。

于是开始写，中途因为预处理边界错了一些，最后成功的调出来了。

然后我就交了，因为两种方法都能过大样例，所以为了保险起见我分了段。

赛后发现第一种方法假了，而且不知道为什么，而且赛时过了大样例，而且打表可以打出来正解，而且原题有skip导致一分没有。

写完 T1 去看 T2，直接做 Nim 可以有 30pts 的分数。

不会优化，弃了。

赛后有人通过对 $a$ 数组去重的手法得到了 40pts。

T3 题意转化一下就是给你一些限制后让你求符合条件的全排列，然后这样可以拿到 10pts。

考虑菊花图的特殊性质，赛后听说其实就是康托展开。但是题目上保证了 $n\le 5000$，所以我们直接 $n^2$ 做就行，对于当前的排列 $p$，我们一位一位考虑。若设 $num$ 为 $1\sim i$ 中没有出现过的数字个数，那么 $i$ 位置上的答案就是 $(n-i)!\cdot num$。

每次直接 $\mathcal{O}(n)$求 $num$，不需要数据结构优化。

写完以后去看 T4，一眼有一种 $\mathcal{O}(k{n}^2)$ 的暴力。

写完以调不过大样例，于是开始思考算法优劣。

我是每次直接枚举该操作哪一位，取影响最大的那个元素删除。这样可以保证正确性，但是需要的变量很多，初值什么的不容易准确，以至于一直调不出来。

想了半天发现求子段和的时候只需要在当前序列中最大的子段中随便删一个就行了，不需要删除最大数，同时这种做法的正确性有保证，同时时间复杂度能优化到 $\mathcal{O}(kn)$，因为求的时候这一位可以在计算答案的时候直接连带着算出来。

然后就写了，发现挂了一次，检查发现是第一次操作的时候直接使用了原序列，改完以后过了样例，然后就走了，此时比赛正好剩下 4min.

赛后发现很多人因为负数取模的问题挂了，但是我没有，因为一个不经意的小操作：

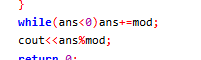
赛后

总分 0+30+25+15=70pts，除了 T1 都是大众分。

感觉没有之前挂分时那种肠子悔青的感觉了，从发现自己挂成 0pts 到现在，我内心没有一点波动。

不知道是为什么，可能是已经看淡了名次，不再那么关心得失了。也不知道是好是坏。