Tarjan算法入门

注：对文章内容有任何问题随时可以提出。
例题方面不再给出，文章仅供了解。

定义

Tarjan 本身就是一个算法，不是一类问题，所以定义中说说所有 Tarjan 问题的共性。

该算法主要用于求图的连通性问题，基于图的深度优先遍历。

在该算法中，有两个很关键的数组 dfn 与 low。

• dfn 数组，中文名时间戳，代表在进行图的深度优先遍历时，依次遍历到的点的顺序，\(dfn_i\) 表示点 \(i\) 被遍历到的顺序，这个数组中的所有值构成一个排列。

• low 数组，中文名追溯值，它的定义在有向图和无向图中略有差异。下面再讲。

还有一些关于图的连通性的概念：

• 割边（桥），在一张联通的无向图上，如果把这条边删去后，这张图会不联通，即整张图是由两个联通子图加上这条边构成。

• 割点，类似割边，在一张联通的无向图上，如果把这个点删去后，这张图会不联通，即整张图是由两个联通子图加上这个点和两条依次连向每一个子图的边构成。

• 边双联通分量，一张无向图上不存在割边的最大联通子图。

• 点双联通分量，一张无向图上不存在割点的最大联通子图。

• 强联通分量，一张有向图上所有点之间能够互相到达的最大联通子图。

• 必经边，一张有向图上两个点之间所有路径上都有的边。

• 必经点，一张有向图上两个点之间所有路径上都有的点。

• 缩点，一种操作，把图上的所有联通分量缩成一个点，缩完以后无向图会变成森林，有向图会变成 DAG。

Tarjan 这东西能求得东西显然非常多，所以一个一个来讲。

无向图问题

low 的定义与求法

它代表的是一些点的 dfn 数组的最小值。具体的，\(low_i\) 表示在搜索树中以下点时间戳的最小值：

• 点 \(i\) 子树中的点。
• 通过一条不在搜索树上的边（返祖边）能够到达 \(i\) 子树中点的点。

那么如何求解这个东西呢？

首先初始化应该为 \(low_i=dfn_i\)，然后考虑如何转移：

遍历 \(i\) 的所有连边 \(j\)。

如果 \(j\) 是搜索树中 \(i\) 子树上的点，显然有方程 \(low_i=\min(low_i,low_j)\)。

如果不是，先判断 \(j\) 在树上是否为 \(i\) 的父亲节点，不是的话说明边 \((i,j)\) 一定不在搜索树中（返祖边），即第二种情况，那么此时 \(low_i=\min(low_i,dfn_j)\)。

对于第二个转移的判断，一般链式前向星存图可以用 \(\oplus 1\) 小技巧，

但是我喜欢用 vector，所以求的时候类似树的遍历，再传一个参数 \(fa\) 代表当前点的父亲，就好判断了。

下面用一张笔者脚搓的图来形象演示两个数组（中括号外是 dfn 的值，中括号里面是 low 的值，带有 ! 的是搜索树上的边）

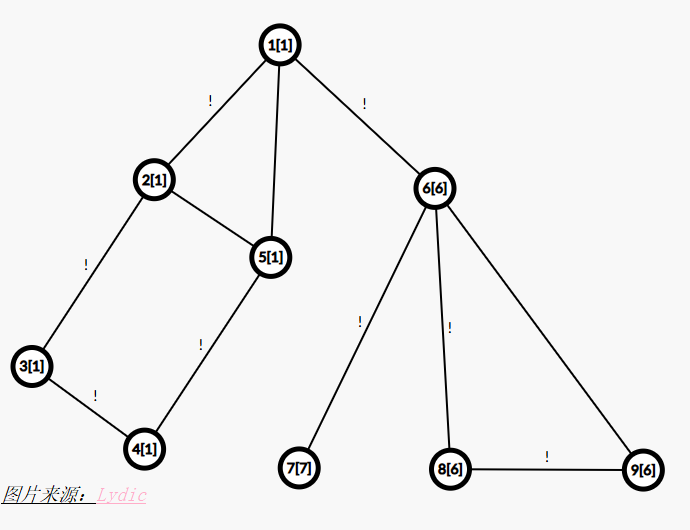
点击查看代码

vector<int> G[maxn];
int dfn[maxn],low[maxn];
int n,m,tot;
void tarjan(int u,int fa)
{
	dfn[u]=low[u]=++tot;
	for(auto y : G[u])
	{
		if(!dfn[y])
		{
			tarjan(y,u);
			low[u]=min(low[u],low[y]);
		}
		else if(y!=fa)low[u]=min(low[u],dfn[y]);
	}
}
……
signed main()
{
……
for(int i=1;i<=n;i++)
	if(!dfn[i])tarjan(i,0);
……
return 0;

无向图的割边（桥）

这就是 Tarjan 算法的神奇之处，能在 \(\mathcal{O}(n)\) 的时间内求出这东西。

尝试利用 dfn 和 low 两个数组。如果一条边 \((x,y)\) 是割边，那么它连接的两个点 \((x,y)\) 的 dfn,low 数组的值有什么特点呢？

首先不在搜索树上的边一定不是割边。

接下来在搜索树上考虑。不妨设 \(dfn_x\lt dfn_y\)，即 \(x\) 是 \(y\) 的父亲节点。根据上面的图我们可以发现，对于所有的桥，一定有 $dfn_x\lt low_y $，这就是桥的判定法则。

简单证明一下：根据两数组的定义，这个式子说明 \(y\) 的子树里没有任何点能够在不经过边 \((x,y)\) 的情况下走到子树外。因为一旦能走到它的 low 值就一定会被比 \(dfn_y\) 小的点更新，证毕。

考虑算法实现，如果要求出所有的割边，那么在上面求 low 数组的时候，只需要对第一个条件判断括号里面的话改一下即可，其余和上面的代码一样。就像这样：

if(!dfn[y])
{
	tarjan(y,u);
	low[u]=min(low[u],low[y]);
	if(low[y]>dfn[u])ans.push_back({u,y});
}

然后就做完了。

无向图的割点

这个和上面的割边很像。我们再次利用这两个数组。

依然在搜索树上考虑。容易发现，一个点 \(x\) 是割点的充要条件是存在至少一个子节点 \(y\) 使得 \(dfn_x\le low_y\)。

特别的，如果 \(x\) 是根节点，那么需要存在至少两个子节点 \(y\) 使得 \(dfn_x\le low_y\)。

这个证明和上面差不多，唯一的区别就是 \(x\) 子树里面的点可以到达 \(x\)。

需要注意的是，在割点的 Tarjan 里面，第二种转移不需要再判断反边。同时在主函数中每次需要重新让 \(root\) 赋值为 \(i\)。

代码实现和割边差不多，长这样：

点击查看代码

vector<int> G[maxn];
int dfn[maxn],low[maxn];
int n,m,tot,root;
vector<int>ans;//存储所有割点
void tarjan(int u,int fa)
{
	dfn[u]=low[u]=++tot;
	int sum=0;
	for(auto y : G[u])
	{
		if(!dfn[y])
		{
			tarjan(y,u);
			low[u]=min(low[u],low[y]);
			if(low[y]>=dfn[u])
			{
				if(u!=root||++sum>1)
					ans.push_back(u);//存储割点
			}
		}
		else low[u]=min(low[u],dfn[y]);
	}
}
……
signed main()
{
……
for(int i=1;i<=n;i++)
	if(!dfn[i])root=i,tarjan(i,0);
……
return 0;

上面的 \(sum\) 既是特判根节点用，也能同时统计删除 \(x\) 后原图会增加几个联通块。需要注意的是遍历结束后，如果 \(x\) 不是根节点，需要 \(sum\leftarrow sum+1\) 才能得到增加的联通块个数（一眼）。

无向图的边双联通分量+缩点

在正常用 Tarjan 求桥的时候，我们对所有的桥用一个 \(bool\) 数组标记为 \(1\)。然后遍历所有点，对于当前的点，递归遍历所有与它相连，不是桥，不在其它边双联通分量里面的边，并全部让其答案数组值统一，即为该边所属的边双联通分量。

全部求完后遍历数组就得到每个店所属的边双联通分量了，如果想求出每个边双里面的点，再搞一个数组专门统计就行了。

缩点的话遍历所有的边，如果边两端的点不在一个边双联通分量里面，就把它们所对应的边双联通分量连边即可。

有点麻烦的是，如果你像我一样喜欢 vector 存图，那么标记边就只能用 map<pair<int,int>,bool> 来搞，这样会使复杂度带上个 \(\log\)，所以需要在存边的时候开一个结构体，并用一个变量 \(cnt\) 记录当前加入的边是第几条，这样就好标记了，就像这样：

G[x].push_back({y,++cnt});
G[y].push_back({x,++cnt});

放一下 Tarjan 做完以后缩点过程的代码：

点击查看代码

……
int c[maxn];//记录每个店所属的边双
int num;//统计边双数量
vector<int> GG[maxn];//新图
void dfs(int x)
{
	c[x]=num;
	for(auto i : G[x])
	{
		int y=i.y,e=i.edge;
		if(c[y]||bridge[e]/*标记数组，在Tarjan里面求解*/)continue;
		dfs(y);
	}
}
……
//主函数内
for(int i=1;i<=n;i++)
{
	if(!c[i])
	{
		num++;
		dfs(i);
	}
}
for(int i=1;i<=n;i++)
{
	for(auto j : G[i])
	{
		if(c[i]==c[j])continue;
		GG[c[i]].push_back(c[j]);
		GG[c[j]].push_back(c[i]);
	}
}

无向图的点双联通分量+缩点

求解点双比边双要复杂一些，因为一个点可能属于多个点双。

为解决此问题，我们需要维护一个栈，同时需要边做 Tarjan 边记录点双。

首先根据定义，如果 \(x\) 是割点，那么判断的时候对于 \(dfn_x\le low_y\) 这个式子中的 \(y\)，从 \(x\) 出发一定能走到 \(y\)。

所以我们在 Tarjan 求割点的时候，对于每一个遍历到的节点，先都入栈。

在找到一个割点 \(x\) 的时候，我们就不断弹出栈中的元素，直到找到 \(y\) 为止，根据定义能发现这中间遇到的所有元素都在一个点双里面，我们用一个一堆 vector 表示每个点双里面的点，存储起来，并标记每一个割点。

有一点细节，我们需要特判一下根是独立点（即没有任何点和它有连边）的情况，如果是的话再开一个点双给它就行。

搞完以后遍历每一个 vector 就可以得到所有点双联通分量。

缩点的时候由于一个割点可能属于多个点双，所以我们单独开一个点双来表示这个割点，并再用一个数组记录其新编号。和边双不一样，建边的时候遍历每一个点双里面的点，如果是割点，那么让该点双和我们对这个割点新建的点双连边，否则用一个数组让这个点属于该点双即可。

由于 Tarjan 里面改动的有点多，所以完整地放一下求点双和缩点的代码，在这里由于不需要标记边，所以 vector 不用开结构体。

点击查看代码

……
vector<int> G[maxn],GG[maxn];//两张图
int dfn[maxn],low[maxn];
int n,m,tot,root;
int num;//统计点双个数
bool cut[maxn];//判断该点是否为割点
int c[maxn];//记录每个点所属的点双
vector<int> dcc[maxn];//存储每一个点双
int new_[maxn];//存储所有割点的新编号
stack<int> st;
void tarjan(int u,int fa)
{
	st.push(u);
	dfn[u]=low[u]=++tot;
	if(u==root&&G[u].empty())return dcc[++num].push_back(u),void();
	int sum=0;
	for(auto y : G[u])
	{
		if(!dfn[y])
		{
			tarjan(y,u);
			low[u]=min(low[u],low[y]);
			if(low[y]>=dfn[u])
			{
				if(u!=root||++sum>1)cut[u]=1;//标记割点
				num++;
				int z;
				do
				{
					z=st.top();st.pop();
                    dcc[num].push_back(z);//存储点双
                    c[z]=num;//记录所属点双
				}while(z!=y);
				dcc[num].push_back(u);
			}
		}
		else low[u]=min(low[u],dfn[y]);
	}
}
signed main() 
{
……
    for(int i=1;i<=n;i++)
	if(!dfn[i])root=i,tarjan(i,0);
	int qw=num;
	for(int i=1;i<=n;i++)
	{
		if(cut[i])new_[i]=++qw;
	}
	for(int i=1;i<=num;i++)
	{
		for(auto j : dcc[i])
		{
			if(cut[j])
			{
				GG[i].push_back(new_[j]);
				GG[new_[j]].push_back(i);
			}
		}
	}
……
}

有向图问题

有向图相对要复杂一点，因为不能单凭边来判断是否联通。

low 的定义与求法

根据刚才说的，既然不能只看边，那么我们如果要判断连通性，就需要存储所有遍历到的点，从而判断两点的连通性。

就像点双一样，我们可以用栈存储所有可能是在同一强连通图中的点，同时出栈的则属于同一强连通图，

在这里 low 根据用途可以直观理解为该强联通分量所在的根节点（搜索树上），根据实现 \(low_x\) 可以定义为以下节点 dfn 的最小值：

• 该节点在栈里面，即可能和 \(x\) 在同一个强联通分量中。

• 在搜索树上该节点可以由 \(x\) 子树中的一个节点通过一条有向边到达。

如果一个节点同时满足这两个条件，则可以用来更新 \(x\) 的 low 值。上面两个条件简单来说就是用来判断 \(x\) 和某节点是否属于一个强联通分量，更新 low 即为找到该强联通分量中 dfn 最小的点，即根。

具体的，我们用一个 vis 数组判断一个点是否在栈中。对于每次访问到的节点，先放进栈里面，因为都有可能产生贡献。

转移求解 low 的时候还是分两种情况，遍历 \(x\) 连的所有 \(y\)，如果 \(y\) 没有访问，则递归 \(y\)，并更新 \(low_x=\min(low_x,low_y)\)。如果 \(y\) 被访问过且在栈中，说明其满足以上条件，更新 \(low_x=\min(low_x,dfn_y)\)。

这样 low 就求完了。

代码如下：

点击查看代码

void tarjan(int x)
{
	s.push(x);
	low[x]=dfn[x]=++tot;
	v[x]=1;
	for(auto y : G[x])
	{
		if(!dfn[y])
		{
			tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(v[y])
		{
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(low[x]==dfn[x])
	{
		int y;
		do
		{
			y=s.top();
			s.pop();
			c[y]=x;
			if(x!=y) vv[x]+=vv[y];
			v[y]=0;
		}while(x!=y);
	}
}

强联通分量+缩点

接着刚才的内容。

如果发现一个点 \(x\) 满足 \(low_x=dfn_x\)，则说明它就是一个强联通分量的根节点。这时候我们就不断弹栈，直到 \(x\) 出栈，因为这时栈中元素显然都和 \(x\) 属于同一个强联通分量。

这样上面的代码解释完了，其中 \(num\) 和 \(c\) 表示的含义和无向图一样，\(scc\) 则用来存储每一个强联通分量。

主函数中对 tarjan 的调用同无向图中求桥的代码。

对于缩点，很简单，遍历所有边，如果两端点不属于一个强联通分量，就让对应的强联通分量连边即可。

代码如下：

for(int i=1;i<=n;i++)
{
    for(auto j : G[i])
    {
    	if(c[i]==c[j])continue;
    	GG[c[i]].push_back(c[j]);
	}
}

总结

Tarjan 的缩点，尤其是有向图，在各种比赛里面考的非常多，因为缩完点以后各种树形DP，拓扑什么的都能搞了，所以 Tarjan 可以理解为一种辅助算法。

耗时整整2Day，支持一下点个赞吧^_。