Kruskal重构树

这东西感觉还挺实用的，所以来讲一下。

定义

简单来说，跑 Kruskal 的时候，我们对于当前要连接的两个点 \(x\) 和 \(y\)，我们建立一个新的节点 \(now\)，并让 \(now\) 作为 \(x,y\) 的父亲节点在一张新图上进行建边，在用并查集合并时改一下合并方式，让 \(fa_x=fa_y=now\) 即可。

这样建完边以后我们可以得到一张图。通过定义可以发现，这张图它是一棵树，这棵树它是一个二叉树，这棵二叉树的所有叶子结点就是原图上的所有点。

性质

下面给一棵重构树：

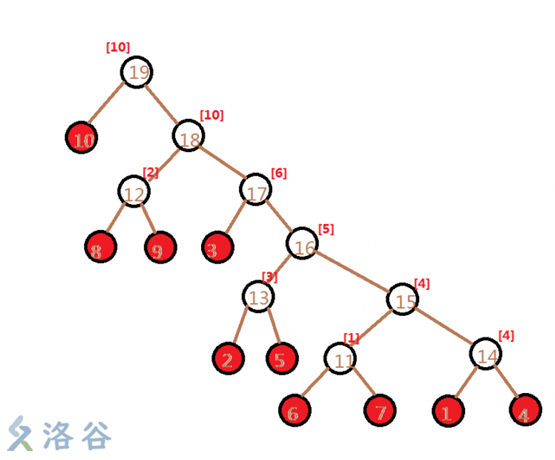
这棵树有一些性质：

• 非叶结点有点权，且为原图边权。

• 每棵子树的叶子结点在原图上都是一个联通块。

• 非叶节点点权（即原图边权）从根节点往下一定是一个大（小）根堆。

• 原图上任意两点间所有路径中最大边权的最小值（最小边权的最大值） = Kruskal 重构树上这两个点 LCA 的点权。

注：后两行括号外代表求的是最小生成树，括号内代表求的是最大生成树。

作为对一切事物都敏感的 OIER，我们可以发现这些性质都有用处。

性质四

直接就给你了，没什么好讲的。

放一手方便以后复制作为代码模板方便理解实现：

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=998244353;
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch^48);ch=getchar();}
	return w*s;
}
const int maxn=5e5+10;
int n,m,k;
struct no
{
	int x,y,v;
	inline friend bool operator < (no x,no y)
	{
		return x.v<y.v;
	}
}edge[maxn];
int fa[maxn];
int gf(int x){return fa[x]==x?x:fa[x]=gf(fa[x]);}
vector<int> G[maxn];
int c[maxn];
int d[maxn],f[maxn][21];
void add(int x,int y)
{
	G[x].push_back(y);
	G[y].push_back(x);
}
void dfs(int y,int fa)
{
	d[y]=d[fa]+1;
	f[y][0]=fa;
	for(int i=1;i<=20;i++)
	f[y][i]=f[f[y][i-1]][i-1];
	for(auto x : G[y])
	{
		if(x==fa)continue;
		dfs(x,y);
	}
}
int lca(int x,int y)
{
	if(d[x]>d[y])swap(x,y);
	int t=d[y]-d[x],j=0;
	while(t)
	{
		if(t&1)y=f[y][j];
		j++;t/=2;
	}
	if(x==y)return y;
	for(int i=20;i>=0;i--)
	{
		if(f[x][i]!=f[y][i])
		{
			x=f[x][i];
			y=f[y][i];
		}
	}
	return f[x][0];
}
signed main()
{	
	cin>>n>>m>>k;
	for(int i=1;i<=m;i++)
	{
		edge[i]={read(),read(),read()};
	}
	for(int i=1;i<=n*2+1;i++)fa[i]=i;
	sort(edge+1,edge+m+1);
	int tot=0,cnt=n;
	for(int i=1;i<=m;i++)
	{
		int fx=gf(edge[i].x),fy=gf(edge[i].y);
		if(fx!=fy)
		{
			c[++cnt]=edge[i].v;
			add(fy,cnt);
			add(fx,cnt);
			fa[fx]=fa[fy]=cnt;
			if(++tot==n-1)break;
		}
	}
	dfs(cnt,0);
	while(k--)
	{
		int x=read(),y=read();
		printf("%lld\n",c[lca(x,y)]);
	}
	return 0;
}

性质二

我们发现图上面的一些能够由子图合并贡献的问题可以在重构树上通过合并子树答案来解决，有一道经典例题：Labyrinth。

配上自己写的题解。

其实一般 Kruskal 重构树问题我们用的都是这个性质（嗯……）

性质三

我们发现点权单调，于是一眼二分倍增。比如这道题，我们可以二分边数，因为单调，所以直接倍增去找就行。

差不多的还有著名的归程。