散知识点总结（持更）
有一些小 trick，专门用一整篇博客来写不太合适，所以都放在这里吧。
逆序对
考试的时候树状数组做法显然比其他的都好写。
考虑每个元素对答案的贡献，我们需要知道在它之前有多少元素比它大。
我们只需要维护一个权值树状数组，在枚举到 \(i\) 的时候查询当前树状数组中的元素有多少比它大，为了方便处理我们倒序枚举，这样相当于求顺序对，方便树状数组计算答案。
每次累加以后只需要把当前元素加进树状数组即可。
for(int i=n;i>=1;i--)
{
ans+=ask(a[i]-1);
add(a[i],1);
}
二进制分组
如果我们有一堆数字，现在要把它们多次分成两组，要求对于每两个数字都至少有一次分在不同的组。
我们考虑二进制，对于每一位，把所有数字这一位为 \(0\) 的分成一组，为 \(1\) 的分成一组，可以证明这样一定能满足上述条件。
简单证明
对于两个不同的数字 \(i,j\)，它们的二进制表达一定至少有一位是不同的，。因此按照上述分组方法一定会至少有一次不在同一组里面。
证毕。
分组的过程很简单，所以给一道例题。
把所有感兴趣的城市进行二进制分组，然后搞两个虚拟点，一个起点一个终点，分别给两组点连 \(0\) 边权的边，然后跑最短路即可。
可爱的代码
#include<bits/stdc++.h>
#define int long long
inline int read()
{
int w=1,s=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
while(isdigit(ch)){s=(s<<1)+(s<<3)+(ch^48);ch=getchar();}
return w*s;
}
using namespace std;
const int maxn=1e6+10;
int T,n,m,k;
int a[maxn];
struct no
{
int y,v;
};
vector<no> G[maxn];
struct dij
{
int y,id;
inline friend bool operator < (dij x,dij y)
{
return x.y>y.y;
}
};
int dis[maxn];
bool vis[maxn];
void dijkstra()
{
memset(dis,0x3f,sizeof dis);
memset(vis,0,sizeof vis);
priority_queue<dij> q;
dis[0]=0;
q.push({0,0});
while(!q.empty())
{
int u=q.top().id;
q.pop();
if(vis[u])continue;
vis[u]=1;
for(auto i : G[u])
{
int y=i.y,v=i.v;
if(dis[u]+v<dis[y])
{
dis[y]=dis[u]+v;
if(!vis[y])
q.push({dis[y],y});
}
}
}
}
signed main()
{
// freopen("tourist.in","r",stdin);
// freopen("tourist.out","w",stdout);
cin>>T;
while(T--)
{
n=read(),m=read(),k=read();
for(int i=0;i<=n;i++)G[i].clear();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),v=read();
G[x].push_back({y,v});
}
for(int i=1;i<=k;i++)a[i]=read();
int ans=0x3f3f3f3f3f3f;
for(int i=0;(1<<i)<=n;i++)
{
G[0].clear();
for(int j=1;j<=k;j++)
{
if(a[j]&(1<<i))G[0].push_back({a[j],0});
else G[a[j]].push_back({n+1,0});
}
dijkstra();
ans=min(ans,dis[n+1]);
for(int j=1;j<=k;j++)
if((!(a[j]&(1<<i))))G[a[j]].pop_back();
G[0].clear();
for(int j=1;j<=k;j++)
{
if(!(a[j]&(1<<i)))G[0].push_back({a[j],0});
else G[a[j]].push_back({n+1,0});
}
dijkstra();
ans=min(ans,dis[n+1]);
for(int j=1;j<=k;j++)
if((a[j]&(1<<i))) G[a[j]].pop_back();
}
printf("%lld\n",ans);
}
return 0;
}
其实简单一想就能发现类似的还有三进制四进制之类的分组，不过这些也不常用，但知道一点是一点。
高维前缀和
这个不是树状数组区间操作的高维前缀和（这个谁用啊），而是维度。
类比ABC366D这道题，先给出一到三维前缀和数组的计算方法：
代码版(复制用)
sum[i]=a[i]+sum[i-1];
sum[i][j]=a[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];
sum[i][j][k]=a[i][j][k]+sum[i][j][k-1]+sum[i][j-1][k]+sum[i-1][j][k]-sum[i][j-1][k-1]-sum[i-1][j][k-1]-sum[i-1][j-1][k]+sum[i-1][j-1][k-1];
稍微懂一点数学的人都已经能看出来规律了。进行 \(n\) 维前缀和的时候，对于前缀和数组的每一维，我们分别对 \(1\sim n\) 个下标进行 \(-1\) 的修改，如果修改个数维奇数，则符号为加号，否则为减号。
容易发现若修改个数为 \(m\)，则共需要修改 \(n\choose m\) 次。因此太高维的一般也不常用，了解即可。
函数嵌套
适用于函数嵌套类型的动态规划进行排序时的比较操作。
对于两个一次函数 \(f(x)=k_1x+b_1\) 和 \(g(x)=k_2x+b_2\)，进行排序的时候如果我们要判断 \(f(g(x))\) 更大还是 \(g(f(x))\) 更大，本质上要比较的两个式子是 \(k_1(k_2x+b_2)+b_1\) 和 \(k_2(k_1x+b_1)+b_2\) 。可以发现展开后的比较与 \(x\) 无关，即我们要比较的是 \(k_1b_2+b_1\) 和 \(k_2b_1+b_2\)。
有了这一点，我们就可以对给定的一堆一次函数进行排序了。
排序代码
inline friend bool operator < (no a, no b)
{
return b.x*a.y+b.y>a.x*b.y+a.y;
}
螺旋矩阵
看下面的一个数组：
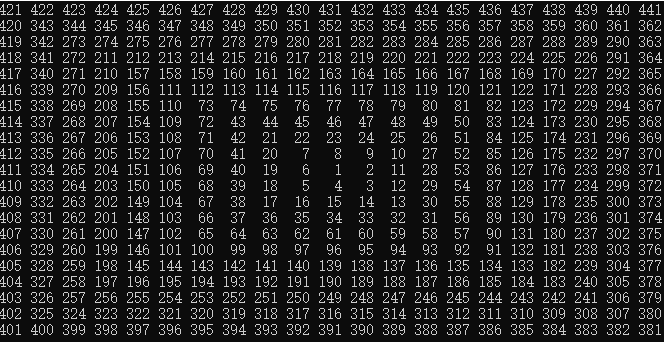
可以发现：它以 \(1\) 为中心，向外按逆时针螺旋填充数字。如果我们设 \(1\) 所在的位置是 \((0,0)\)，向右向上为正方向建立平面直角坐标系，那么 \((x,y)\) 位置表示的数字是什么呢？
我们分四个象限考虑，我的思路（可能不是最简单）是先看看当前坐标是否还属于单增的那部分，如果不是计算差了几个，然后计算每旋转一次需要多少个，最后套个等差数列（写了3h，md细节）。
点击查看代码
int calc(int x,int y)
{
int ans=0;
if(x>=0)ans=4*x*x-3*x+1;
else ans=4*x*x-x+1;
if(x>=0)
{
if(y>=0)
{
if(y<=x)
{
ans+=y;
return ans;
}
int delta=y-x-1;
ans+=x;
ans+=4*(2*x+delta)*(delta+1)+3*(delta+1);
return ans;
}
if(abs(y)<x)
{
y*=-1;
ans-=y;
return ans;
}
ans-=(x-1);
int delta=abs(y)-x;
y=-x+1;
ans+=(-4)*(2*y-delta)*(delta+1)+7*(delta+1);
return ans;
}
if(y>=0)
{
if(abs(x)>=y)
{
ans-=y;
return ans;
}
int delta=y-abs(x)-1;
ans+=x;
x=abs(x);
ans+=4*(2*x+delta)*(delta+1)+3*(delta+1);
return ans;
}
if(abs(x)>=abs(y))
{
ans+=abs(y);
return ans;
}
int delta=abs(y)-abs(x);
x=abs(x);
ans+=x;
ans=ans+4*delta*(2*x+delta+1)-delta;
return ans;
}
上取整
逆取模
使得 \(b\mid (a+d)\) 的最小 \(d\) 为 \(((b-a)\mod b+b)\mod b\)。
