线段树扩展学习

标记可持久化

这个很好理解，在进行区间修改的时候，不下传懒标记，查询的时候直接对每一层再进行处理即可。

这个主要用于线段树分治和可持久化方面的内容，也能优化常数。不过容易使节点信息溢出，所以一般不用。

动态开点

这种线段树主要用于优化空间复杂度。就是对于下标，不用常规方法存储节点的左右儿子，而用一个单独的变量 \(tot\) 来存储。

这点大家作为资深 OIER 一定都懂，下面说一下代码方面和普通线段树的区别。

在写函数的时候，需要额外定义当前节点所代表的区间的信息。

本人喜欢用结构体存储，所以需要在结构体里面增加 \(lc,rc\) 代表儿子下标，并且用宏定义优化代码长度。在调用的时候将 \(t_{t_{p*2}.lc}\) 改为 \(t_{lc(p)}\) 即可，右儿子同理。

懒标记部分判断一下 \(lc,rc\) 是否被赋值，如果没有让 \(tot++\) 然后再去赋值就行了。

区修部分需要额外开一个变量 \(p\) 来表示当前节点编号，函数里面用实参调用 \(p\)，这样方便对 \(lc,rc\) 进行赋值，其余不变。

查询部分只需要在最开始判断一下当前编号是否已经被赋值，如果没有直接返回。这也是动态开点线段树优化空间的直接表现。

稍微放下洛谷线段树模板一的代码，最开始的时候忘记 \(upd\) 了，查了好久才发现我太菜了。

最后，动态开点线段树的空间应该开到 \(Q\log V\)，一般题目为 \(5\times 10^6\sim 1\times 10^7\) 左右。

点击查看代码

#include<bits/stdc++.h>
#define int long long
const int maxn=1e6+10;
using namespace std;
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=s*10+(ch-'0');ch=getchar();}
	return w*s;
}
int n,Q,tot,st;
struct no
{
	int d,add;
	int lc,rc;
	#define lc(x) t[x].lc
	#define rc(x) t[x].rc
}t[maxn<<2];
void upd(int p)
{
	t[p].d=t[lc(p)].d+t[rc(p)].d;
}
void spread(int p,int tl,int tr)
{
	if(!t[p].add)return ;
	int mid=(tl+tr)>>1;
	if(!lc(p))t[p].lc=++tot;
	if(!rc(p))t[p].rc=++tot;
	t[lc(p)].d+=t[p].add*(mid-tl+1);
	t[rc(p)].d+=t[p].add*(tr-mid);
	t[lc(p)].add+=t[p].add;
	t[rc(p)].add+=t[p].add;
	t[p].add=0;
}
void add(int &p,int tl,int tr,int l,int r,int k)
{
	if(!p) p=++tot;
	if(tl>=l&&tr<=r)
	{
		t[p].d+=k*(tr-tl+1);
		t[p].add+=k;
		return ;
	}
	spread(p,tl,tr);
	int mid=(tl+tr)>>1;
	if(mid>=l)add(lc(p),tl,mid,l,r,k);
	if(mid<r)add(rc(p),mid+1,tr,l,r,k);
	upd(p);
}
int ask(int p,int tl,int tr,int l,int r)
{
	if(!p)return 0;
	if(tl>=l&&tr<=r)return t[p].d;
	spread(p,tl,tr);
	int mid=(tl+tr)>>1,ma=0;
	if(mid>=l)ma+=ask(lc(p),tl,mid,l,r);
	if(mid<r)ma+=ask(rc(p),mid+1,tr,l,r);
	return ma;
}
signed main()
{
	cin>>n>>Q;
	for(int i=1;i<=n;i++)
	{
		int x=read();
		add(st,1,n,i,i,x);
	}
	while(Q--)
	{
		int opt=read(),l=read(),r=read();
		if(opt==1){int k=read();add(st,1,n,l,r,k);}
		else printf("%lld\n",ask(st,1,n,l,r));
	}
	return 0;
}

线段树合并

这种方法一般处理树上线段树的问题，即合并两个节点的线段树信息。

其实很简单，对两个线段树维护的信息进行合并，需要更新下标和维护内容。

下标的话只需要特判一下是否存在，然后不存在的话新开一个节点就行，维护内容的话就正常处理，复杂度单 \(\log\)。

随便放一个众数的代码：

点击查看代码

}
int merge(int x,int y,int l,int r)
{
    if(!x||!y)return x+y;
    if(l==r)
    {
        t[x].sum+=t[y].sum;
        return x;
    }
    int mid=(l+r)>>1;
    t[x].l=merge(t[x].l,t[y].l,l,mid);
    t[x].r=merge(t[x].r,t[y].r,mid+1,r);
    upd(x);
    return x;
}

\(\Large \color{pink}{什么？你还是不会，那就接着看}\)
为了能够直观简单的理解线段树合并，我找到了一道很好的题目，完全不需要其他树剖之类的技巧，纯粹的合并：[ABC365G] AtCoder Office。

这道题合并的时候如果一颗线段树的区间完全覆盖，那么答案因为要取交集，所以显然这一部分的答案就是另一颗线段树在这个区间上的长度。

值得注意的是，这样无法通过本题，还需要记忆化等优化（具体见代码）。所以这道题仅仅是帮助理解线段树合并的含义。

点击查看代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
#define Ls(x) (x<<1)
#define Rs(x) (x<<1|1)
#define Mid (L+R>>1)
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=s*10+(ch-'0');ch=getchar();}
	return w*s;
}
const int maxn=3e5+100;
const int mod=998244353;
const int inf=1e9+7;	
int n,m,Q;
vector<int> v[maxn];
map<pair<int,int>,int> mp;
int rt[maxn],tot;
struct Seg
{
	int l,r,d;
	#define lc(p) t[p].l
	#define rc(p) t[p].r
}t[maxn<<7];
void upd(int p){t[p].d=t[lc(p)].d+t[rc(p)].d;}
void change(int &p,int tl,int tr,int l,int r)
{
	if(!p)p=++tot;
	if(tl>=l&&tr<=r)
	{
		t[p].d=tr-tl+1;
		return ;
	}
	int mid=(tl+tr)>>1;
	if(mid>=l)change(lc(p),tl,mid,l,r);
	if(mid<r)change(rc(p),mid+1,tr,l,r);
	upd(p);
}
int ask(int x,int y,int l,int r)
{
	if(!x||!y)return 0;
	if(t[x].d==r-l+1)return t[y].d;
	if(t[y].d==r-l+1)return t[x].d;
	int mid=(l+r)>>1;
	return ask(lc(x),lc(y),l,mid)+ask(rc(x),rc(y),mid+1,r);
}
signed main()
{
#ifdef Lydic
	freopen(".in","r",stdin);
	freopen(".out","w",stdout);
//  #else
//   	freopen("Stone.in","r",stdin);
//   	freopen("Stone.out","w",stdout);
#endif
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int t=read(),p=read();
		v[p].push_back(t);
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<v[i].size();j+=2)
		{
			change(rt[i],1,inf,v[i][j],v[i][j+1]-1);
			// cout<<v[i][j]<<' '<<v[i][j+1]<<endl;
		}
	}
	Q=read();
	while(Q--)
	{
		int x=read(),y=read();
		if(x>y)swap(x,y);
		if(mp.find({x,y})!=mp.end())printf("%lld\n",mp[{x,y}]);
		else printf("%lld\n",mp[{x,y}]=ask(rt[x],rt[y],1,inf));
	}
	return 0;
}

线段树优化建图

这个比前面的稍微难一点，不过也还行。

放一道模板题。

考虑建图的时候如果需要让一个节点和一个区间内的所有节点连边，那么正常情况下会爆时间。

所以我们把连边操作放到线段树里面。连边时，我们只需要让节点对对应区间连边即可。

但是如果有无向边的话，一颗线段树会乱套，所以我们建两棵线段树，分别存储点连向线段树区间节点和线段树区间结点连向点的边。下文我们称它们分别为入树和出树。

最开始的时候，我们让入树中左右节点连向它的两个儿子，出树则让儿子连向它的父亲节点，都是有向边，边权为 \(0\)。同时让两棵树对应位置的所有叶节点也连上边权为 \(0\) 的无向边，这样两棵线段树就完成了初始化。

对于编号的话，我们让入树的节点编号正常搞，出树则根据数据范围加上一个偏移量 \(k\)。对于所有叶节点，我们用一个数组 \(id\) 表示原数组中的位置在入树中所对应的叶节点编号，然后对于出树，叶节点编号直接就是 \(id_i+k\) 了。

以点连向区间为例，我们让出树中对应的叶节点连向入树中覆盖该区间的节点，另一种操作同理。

模板题要求跑单源最短路，那么我们找到起点在出树中所对的编号，然后正常 dijkstra 即可。

当然，我们还有一道模板题。这道题是区间连区间，我们只需要对第一个区间所有需要连的点存进一个数组，然后对于第二个区间，递归找的时候每找到一个就对这个数组里面的所有点进行连边，这样建边的复杂度是 \(\mathcal{O}(mlog^2n)\) 的，常数比较大。

第一题的代码

#include<bits/stdc++.h>
#define int long long
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=(s<<1)+(s<<3)+(ch^48);ch=getchar();}
	return w*s;
} 
using namespace std;
const int maxn=2e6+100;
int n,m,s,k;
struct Seg
{
	int l,r;
}t[3000100];
struct no
{
	int y,v;
};
vector<no> G[maxn];
void add(int x,int y,int v)
{
	G[x].push_back({y,v});
}
int id[maxn];
void build(int p,int l,int r)
{
	t[p].l=l,t[p].r=r;
	if(l==r)
	{
		id[l]=p;
		return ;
	}
	int mid=(l+r)>>1;
	add(p,p*2,0);add(p,p*2+1,0);
	add(p*2+k,p+k,0);add(p*2+1+k,p+k,0);
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
}
void change(int p,int l,int r,int x,int v,int opt)
{
	if(t[p].l>=l&&t[p].r<=r)
	{
		if(opt==2)add(x+k,p,v);
		else add(p+k,x,v);
		return ;
	}
	int mid=(t[p].l+t[p].r)>>1;
	if(l<=mid)change(p*2,l,r,x,v,opt);
	if(mid<r)change(p*2+1,l,r,x,v,opt);
}
struct dii
{
	int y,id;
	inline friend bool operator < (dii x,dii y)
	{
		return x.y>y.y;
	}
};
int dis[maxn];
bool vis[maxn];
void distla(int s)
{
	memset(dis,0x3f,sizeof dis);
	priority_queue<dii> q;
	dis[s]=0;
	q.push({0,s});
	while(!q.empty())
	{
		int u=q.top().id;
		q.pop();
		if(vis[u])continue;
		vis[u]=1;
		for(auto i : G[u])
		{
			int y=i.y,v=i.v;
			if(dis[u]+v<dis[y])
			{
				dis[y]=dis[u]+v;
				if(!vis[y])
				q.push({dis[y],y});
			}
		}
	}
}
signed main()
{
	cin>>n>>m>>s;
	k=5e5;
	build(1,1,n);
	for(int i=1;i<=n;i++)
	{
		add(id[i],id[i]+k,0);
		add(id[i]+k,id[i],0);
	}
	for(int i=1;i<=m;i++)
	{
		int opt=read(),x=read();
		if(opt==1)
		{
			int y=read(),v=read();
			add(id[x]+k,id[y],v);
		}
		else if(opt==2||opt==3)
		{
			int l=read(),r=read(),v=read();
			change(1,l,r,id[x],v,opt);
		}
	}
	distla(id[s]+k);
	for(int i=1;i<=n;i++)
	cout<<(dis[id[i]]==0x3f3f3f3f3f3f3f3fll?-1:dis[id[i]])<<' ';
	return 0;
}

第二题的代码

#include<bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
#define int long long
using namespace std;
// using namespace  __gnu_pbds;
// tree<int,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update> tr;//从小到大
// int findnum(int k){auto it=tr.find_by_order(k-1);return ((it!=tr.end())?(*it):1e9+7);}//查元素
// int findrank(int x){return tr.order_of_key(x)+1;}//查排名
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=s*10+(ch-'0');ch=getchar();}
	return w*s;
}
const int mod=1e9+7;
const int maxn=1e6+10;
const int inf=1e17;
const double eps=1e-10;
int n,m,s,k;
struct Seg
{
	int l,r;
}t[5000100];
struct no
{
	int y,v;
};
vector<no> G[maxn];
void add(int x,int y,int v)
{
	G[x].push_back({y,v});
}
int id[maxn];
void build(int p,int l,int r)
{
	t[p].l=l,t[p].r=r;
	if(l==r)
	{
		id[l]=p;
		return ;
	}
	int mid=(l+r)>>1;
	add(p,p*2,0);add(p,p*2+1,0);
	add(p*2+k,p+k,0);add(p*2+1+k,p+k,0);
	build(p*2,l,mid);
	build(p*2+1,mid+1,r);
}
vector<int> vv;
void change(int p,int l1,int r1)
{
	if(t[p].l>=l1&&t[p].r<=r1)
	{
		vv.push_back(p);
		return ;
	}
	int mid=(t[p].l+t[p].r)>>1;
	if(l1<=mid)change(p*2,l1,r1);
	if(mid<r1)change(p*2+1,l1,r1);
}
void change2(int p,int l1,int r1)
{
	if(t[p].l>=l1&&t[p].r<=r1)
	{
		for(auto i : vv)
		{
			add(i+k,p,1);
			add(p+k,i,1);
		}
		return ;
	}
	int mid=(t[p].l+t[p].r)>>1;
	if(l1<=mid)change2(p*2,l1,r1);
	if(mid<r1)change2(p*2+1,l1,r1);
}
struct dii
{
	int y,id;
	inline friend bool operator < (dii x,dii y)
	{
		return x.y>y.y;
	}
};
int dis[maxn];
bool vis[maxn];
void distla(int s)
{
	memset(dis,0x3f,sizeof dis);
	priority_queue<dii> q;
	dis[s]=0;
	q.push({0,s});
	while(!q.empty())
	{
		int u=q.top().id;
		q.pop();
		if(vis[u])continue;
		vis[u]=1;
		for(auto i : G[u])
		{
			int y=i.y,v=i.v;
			if(dis[u]+v<dis[y])
			{
				dis[y]=dis[u]+v;
				if(!vis[y])
				q.push({dis[y],y});
			}
		}
	}
}
signed main()
{
#ifdef Lydic
    freopen(".in","r",stdin);
    freopen(".out","w",stdout);
#endif
	cin>>n>>m>>s;
	k=5e5+1;
	build(1,1,n);
	for(int i=1;i<=n;i++)
	{
		add(id[i],id[i]+k,0);
		add(id[i]+k,id[i],0);
	}
	for(int i=1;i<=m;i++)
	{
		int l1=read(),r1=read(),l2=read(),r2=read();
		vv.clear();
		change(1,l1,r1);
		change2(1,l2,r2);
	}
	distla(id[s]+k);
	for(int i=1;i<=n;i++)
	cout<<(dis[id[i]]==0x3f3f3f3f3f3f3f3fll?-1:dis[id[i]])<<endl;
	return 0;
}

吉司机线段树

这种线段树主要维护区间最值修改。

具体的，给一道例题（luogu的例题维护的东西太多了，作者懒，所以不用了）。

具体的，在这道题里面，线段树对每个节点维护四个信息。分别是最大值 \(mx\)，最大值个数 \(smax\)，次大值 \(rmax\)，区间和 \(sum\)。

对于区间最值操作，即形如 \(\forall x \in [l,r]，a_x=min(a_x,t)\)，我们分三种情况讨论：

若 \(mx\leq t\)，则不操作。

若 \(rmax\lt t\lt mx\)，则修改 \(sum+=smax\times (t-mx)\) 和 \(mx=t\)，并进行懒标记。

否则不更新，直接递归。

其余的就是正常操作了。

不同的地方主要是 \(spread\) 函数，取最小值时信息的修改和 \(update\) 函数，这里放一下这几个东西的代码和它们对应的位置（伪代码）。

点击查看代码

void update(int p) 
{  
	t[p].sum=t[p*2].sum+t[p*2+1].sum;
	if(t[p*2].mx==t[p*2+1].mx) 
	{
		t[p].mx=t[p*2+1].mx;
		t[p].rmax=max(t[p*2].rmax,t[p*2+1].rmax);
		t[p].smax=t[p*2].smax+t[p*2+1].smax;
	} 
	else if(t[p*2].mx>t[p*2+1].mx) 
	{
		t[p].mx=t[p*2].mx;
		t[p].rmax=max(t[p*2].rmax,t[p*2+1].mx);
		t[p].smax=t[p*2].smax;
	} 
	else 
	{
		t[p].mx=t[p*2+1].mx;
		t[p].rmax=max(t[p*2].mx,t[p*2+1].rmax);
		t[p].smax=t[p*2+1].smax;
	}
}
void work(int p,int k)
{
	if(t[p].mx<=k)return ;
	/*剩下两种情况在这里是等价的*/
	t[p].sum+=(k-t[p].mx)*t[p].smax;
	t[p].mx=k;
	t[p].add=k;
}
void spread(int p)
{
	if(!t[p].add)return ;
	work(p*2,t[p].add);work(p*2+1,t[p].add);
	t[p].add=0;
}
void change()
{
	if()
	{
		work();
		return ;
	}
	spread();
	if()change();
	if()change();
	update();
}
int askmx()
{
	if()
	{
		return t[p].mx;
	}
	spread();
	askmx();
	askmx();
}
int asksum()
{
	if()
	{
		return t[p].sum;
	}
	spread();
	asksum();
	assum();
}

扫描线

这玩意网上一堆，也好理解，所以不写了。

李超线段树

咕了三个月终于更了（作者太废物了）。

这玩意太实用啦。

OI-WiKi 上面讲的就是一坨。

这个其实很好理解。以这道例题为例，我们可以先考虑直线的情况。

我们让线段树的每个节点存储一个结构体，表示这段区间中点处最优的线段表达式。此时如果是叶节点，显然就是答案，不是的话也可以帮助我们递归。

插入的时候，如果新直线在中点处比原直线更优，我们就直接交换两直线去更新该节点的答案。然后因为要下传懒标记，所以需要考虑新直线对左右哪段区间会产生影响，只去下传有影响的那半部分从而保证复杂度。分别对左右端点考虑，由于直线具有单调性，参考零点存在性定理的思想可以发现只有当新直线此端点的的值大于原直线此端点的值时，该区间才需要下传标记，另一个区间一定全部都是原直线最优。这样只递归一个区间的话可以保证复杂度是单 \(\log\) 级的。

查询的时候就正常查，复杂度还是单 \(\log\)。

那么回到这道题，编号的话显然可以跟着一起处理出来。对于线段的话可以用一个小技巧，在计算这条线段在某点的取值时，如果不在定义域里面，直接返回极小值。这其实等价于该线段被分成了 \(\log\) 条直线，这样一次修改的复杂度是 \(\log^2\)。

这道题的细节是真TM多啊。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=s*10+(ch-'0');ch=getchar();}
	return w*s;
}
const int mod=998244353;
const int maxn=1e6+10;
const int inf=1e9+7;
const int R=50000;
int Q;
struct Seg
{
	double k,b;
	int l,r;
	int id;
	inline double operator () (int x)
    {return (x>=l&&x<=r?k*x+b:-inf);}
};
struct LC
{
	int l,r;
	Seg d;
	#define lc(p) t[p].l
	#define rc(p) t[p].r
}t[maxn<<2];
struct no
{
	double y;
	int id;
};
no maxx(no a,no b)
{
	if(a.y-b.y>1e-8)return a;
	else if(b.y-a.y>1e-8)return b;
	else return (a.id>b.id?b:a);
}
int tot,rt;
void change(int &p,int tl,int tr,Seg k)
{
    if(tl>=k.l&&tr<=k.r)
    {
        if(!p)
        {
            p=++tot;
            t[p].d=k;
            return ;
        }
        int mid=(tl+tr)>>1;
        if(k(mid)-t[p].d(mid)>1e-8||fabs(k(mid)-t[p].d(mid))<1e-8&&k.id<t[p].d.id)swap(k,t[p].d);
        if(k(tl)-t[p].d(tl)>1e-8||fabs(k(tl)-t[p].d(tl))<1e-8&&k.id<t[p].d.id)change(lc(p),tl,mid,k);
        if(k(tr)-t[p].d(tr)>1e-8||fabs(k(tr)-t[p].d(tr))<1e-8&&k.id<t[p].d.id)change(rc(p),mid+1,tr,k);
        return ;
    }
    else
    {
        if(!p)p=++tot;
        int mid=(tl+tr)>>1;
        if(mid>=k.l)change(lc(p),tl,mid,k);
        if(mid<k.r)change(rc(p),mid+1,tr,k);
    }
}
no ask(int p,int tl,int tr,int k)
{
	// if(!p)return {0,0};     
	no res={t[p].d(k),t[p].d.id};
    if(tl==tr)return res;
	int mid=(tl+tr)>>1;
	if(mid>=k)res=maxx(res,ask(lc(p),tl,mid,k));
	else res=maxx(res,ask(rc(p),mid+1,tr,k));
	return res;
}
signed main()
{
#ifdef Lydic
	freopen(".in", "r", stdin);
	freopen(".out", "w", stdout);
//  #else
//   	freopen("Stone.in","r",stdin);
//   	freopen("Stone.out","w",stdout);
#endif
	cin>>Q;
	int la=0,idd=0;
	while(Q--)
	{
		int opt=read();
		if(opt==0)
		{
			int x=(read()+la-1)%39989+1;
			printf("%lld\n",la=ask(rt,1,R,x).id);
            // for(int i=1;i<=10;i++)cout<<ask(rt,1,R,i).id<<' ';cout<<endl;
		}	
		else
		{
			idd++;
			int sx=(read()+la-1)%39989+1,sy=(read()+la-1)%1000000000+1;
			int tx=(read()+la-1)%39989+1,ty=(read()+la-1)%1000000000+1;
			Seg x;
			if(sx>tx){swap(sx,tx);swap(sy,ty);}
			if(sx==tx)x={0,(double)max(sy,ty),sx,tx,idd};
			else
			{
				double k=(ty-sy)*1.0/((tx-sx)*1.0);
				double b=sy*1.0-sx*k*1.0;
				x={k,b,sx,tx,idd};
			}
			change(rt,1,R,x);
		}
	}
	return 0;
}

李超线段树最广泛的应用就是动态规划的斜率优化。挑一道简单直观的题目：[CEOI2017] Building Bridges。

这道题可以一眼看出 DP 转移方程为：

\[dp_i=\min_{j=1}^{i-1}dp_j+h_i^2+h_j^2-2h_ih_j+sum_{i-1}-sum{j} \]

然后我们尝试分离参数，可以得到：

\[dp_i=h_i^2+sum_{i-1}+\min_{j=1}^{i-1}(-2h_j\times h_i+dp_j+h_j^2-sum_{j}) \]

考虑 \(\min\) 函数里的东西，我们把 \(h_i\) 看做自变量，那么括号内的可以看做一个一次函数。我们把这些东西插到一颗李超树里面，就可以维护值了。

下面的代码也可以当做模板代码使用：

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=s*10+(ch-'0');ch=getchar();}
	return w*s;
}
const int mod=998244353;
const int maxn=2e5+10;
const int inf=1e14+7;
const int R=2e6+10;
int Q;
struct Seg
{
	int k,b;
	inline int operator () (int x){return k*x+b;}
}x[maxn];
struct LC
{
	int l,r;
	Seg d;
	#define lc(p) t[p].l
	#define rc(p) t[p].r
    LC()
    {
        d.k=0;
        d.b=inf;
    }
}t[maxn<<2];
int tot,rt;
void change(int &p,int tl,int tr,Seg k)
{
    if(!p)p=++tot; 
    if(tl==tr)
    {
        int x1=t[p].d.k*tl+t[p].d.b;
        int x2=k.k*tl+k.b;
        if(x2<x1)t[p].d=k;
        return ;
    }
    int mid=(tl+tr)>>1;
    if(k(mid)<t[p].d(mid))swap(k,t[p].d);
    if(k(tl)<t[p].d(tl))change(lc(p),tl,mid,k);
    if(k(tr)<t[p].d(tr))change(rc(p),mid+1,tr,k);
    return ;
}
int ask(int p,int tl,int tr,int k)
{
    int res=t[p].d(k);
    if(tl==tr)return res;
    int mid=(tl+tr)>>1;
    if(mid>=k)res=min(res,ask(lc(p),tl,mid,k));
    else res=min(res,ask(rc(p),mid+1,tr,k));
    return res;
}
int n,h[maxn],w[maxn],dp[maxn];
int sum[maxn];
signed main()
{
#ifdef Lydic
	freopen(".in", "r", stdin);
	freopen(".out", "w", stdout);
//  #else
//   	freopen("Stone.in","r",stdin);
//   	freopen("Stone.out","w",stdout);
#endif
	cin>>n;
    for(int i=1;i<=n;i++)h[i]=read();
    for(int i=1;i<=n;i++)w[i]=read(),sum[i]=sum[i-1]+w[i];
    dp[1]=0;
    x[0].b=inf;
    x[1].k=-2*h[1];
    x[1].b=h[1]*h[1]-w[1];
    change(rt,0,R,x[1]);
    for(int i=2;i<=n;i++)
    {
        dp[i]=h[i]*h[i]+sum[i-1]+ask(rt,0,R,h[i]);
        x[i]={-2*h[i],dp[i]+h[i]*h[i]-sum[i]};
        change(rt,0,R,x[i]);
    }
    cout<<dp[n];
	return 0;
}

关于李超线段树的一点小拓展

我们发现，李超线段树的基本实现依赖于函数的单调性，所以我们大胆拓展，即它可以维护大部分单调函数的信息。

所以可以给出一道例题：[POI2011] Lightning Conductor

这道题稍微变一下式子可以得到：

\[p_{min}=-a_i+\max_{j=1}^{n}(a_j+\sqrt{|i-j|}) \]

然后 \(\max\) 里面的东西可以看做一个关于 \(i\) 的一个函数。这个函数画出来大概长这样：

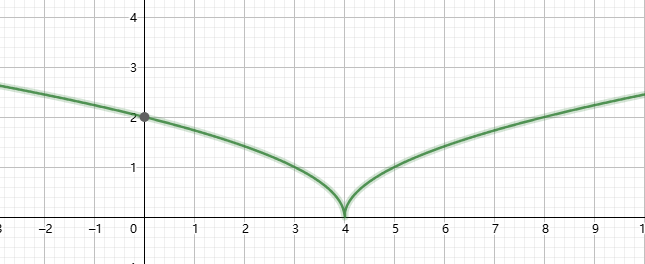
它好像不单调，怎么办呢？很简单，把绝对值拆开，分类讨论跑两次就可以啦。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
	int w=1,s=0;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch)){s=s*10+(ch-'0');ch=getchar();}
	return w*s;
}
const int mod=998244353;
const int maxn=5e5+10;
const int inf=1e9+7;
const int R=1e12+10;
const double eps=1e-8;
bool pro;
struct Seg
{
	double k,b;
	inline double operator () (int x)
    {
        double y=((!pro)?x-b:b-x);
        if(y<=0.0)return -inf;
        return k+sqrt(y);
    }
}x[maxn];
struct LC
{
	int l,r,d;
	#define lc(p) t[p].l
	#define rc(p) t[p].r
}t[maxn<<2];
int tot,rt;
void change(int &p,int tl,int tr,int k)
{
    if(!p){p=++tot;t[p].d=k;return ;}
    int mid=(tl+tr)>>1;
    if(x[k](mid)>x[t[p].d](mid)+eps)swap(k,t[p].d);
    if(x[k](tl)>x[t[p].d](tl)+eps)change(lc(p),tl,mid,k);
    if(x[k](tr)>x[t[p].d](tr)+eps)change(rc(p),mid+1,tr,k);
    return ;
}
double ask(int p,int tl,int tr,int k)
{
    if(!p)return 0;
    double res=x[t[p].d](k);
    if(tl==tr)return res;
    int mid=(tl+tr)>>1;
    if(mid>=k)res=max(res,ask(lc(p),tl,mid,k));
    else res=max(res,ask(rc(p),mid+1,tr,k));
    return res;
}
int n,a[maxn];
int anx[maxn],any[maxn];
signed main()
{
#ifdef Lydic
	freopen(".in", "r", stdin);
	freopen(".out", "w", stdout);
//  #else
//   	freopen("Stone.in","r",stdin);
//   	freopen("Stone.out","w",stdout);
#endif
	cin>>n;
    for(int i=1;i<=n;i++)a[i]=read();
    for(int i=1;i<=n;i++)x[i]={(double)a[i],(double)i};
    for(int i=1;i<=n;i++)
    {
        anx[i]=ceil(ask(rt,1,n,i));
        change(rt,1,n,i);
    }
    for(int i=1;i<=tot;i++)t[i]={0,0,0};
    tot=0;rt=0;pro=1;
    for(int i=n;i>=1;i--)
    {
        any[i]=ceil(ask(rt,1,n,i));
        change(rt,1,n,i);
    }
    for(int i=1;i<=n;i++)
    {
        printf("%lld\n",max(max(anx[i],any[i])-a[i],0ll));
    }
	return 0;
}