CGAffineTransform 放射变换
矩阵乘法
A B相乘要A的列数等于B的行数才有定义，结果是一个 A行B列的矩阵C，C的每个元素值为A对应的行与B对应的列的元素乘积的和
具体看这里
原理
CGAffineTransform
CGAffineTransform 的结构如下
struct CGAffineTransform {
CGFloat a;
CGFloat b;
CGFloat c;
CGFloat d;
CGFloat tx;
CGFloat ty;
};
typedef struct CGAffineTransform CGAffineTransform;
它其实表示的是一个矩阵
因为最后一列总是是(0,0,1)，所以有用的信息就是前面两列
对一个view进行仿射变化就相当于对view上的每个点做一个乘法
结果就是
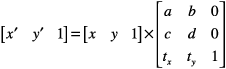
基本上就是如果不看c和b的话
a表示x水平方向的缩放，tx表示x水平方向的偏移
d表示y垂直方向的缩放，ty表示y垂直方向的偏移
如果b和c不为零的话，那么视图肯定发生了旋转
常量
CGAffineTransformIdentity const CGAffineTransformCGAffineTransformIdentity;
这个就是没有变化的最初的样子
创建一个仿射矩阵
- CGAffineTransformMake 直接赋值来创建
- CGAffineTransformMakeRotation 设置角度来生成矩阵
- 结果就是
- CGAffineTransformMakeScale 设置缩放，及改变a、d的值
- CGAffineTransformMakeTranslation 设置偏移
改变已经存在的放射矩阵
- CGAffineTransformTranslate 原始的基础上加上偏移
- CGAffineTransformScale加上缩放
- CGAffineTransformRotate加上旋转
- CGAffineTransformInvert 反向的仿射矩阵比如（x，y）通过矩阵t得到了（x',y'）那么通过这个函数生成的t'作用与（x',y'）就能得到原始的(x,y)
- CGAffineTransformConcat 通过两个已经存在的放射矩阵生成一个新的矩阵t' = t1 * t2
应用仿射矩阵
- CGPointApplyAffineTransform 得到新的点
- CGSizeApplyAffineTransform 得到新的size
- CGRectApplyAffineTransform 得到新的rect
评测矩阵
- CGAffineTransformIsIdentity 是否是CGAffineTransformIsIdentity
- CGAffineTransformEqualToTransform 看两个矩阵是否相等
还原transform
缩放
水平方向缩放
sqrt(a^2+c^2)
垂直方向缩放
sqrt(b^2+d^2)
旋转的角度
tan(angle) = b / a
偏移 tx， ty
CGAffineTransform makeTransform(CGFloat xScale, CGFloat yScale,
CGFloat theta, CGFloat tx, CGFloat ty)
{
CGAffineTransform transform = CGAffineTransformIdentity;
transform.a = xScale * cos(theta);
transform.b = yScale * sin(theta);
transform.c = xScale * -sin(theta);
transform.d = yScale * cos(theta);
transform.tx = tx;
transform.ty = ty;
return transform;
}
应用
放射矩阵一个常用的情形就是根据用户的手势来相应的改变视图的变换
UIPanGestureRecognizer 对应位移
UIPinchGestureRecognizer 对应缩放
UIRotationGestureRecognizer 对应旋转
通常如果需要看到实时的手指移动视图就相应的变换的技巧就是，每次接收到对应的gesture时间就相应的改变view的transform，然后吧这个gesture对应的translation、scale、rotation置为初始值。
转自Jlins博客 博客地址
