KS-检验(Kolmogorov-Smirnov test)
转:https://www.cnblogs.com/arkenstone/p/5496761.html
Kolmogorov-Smirnov是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。其原假设H0:两个数据分布一致或者数据符合理论分布。D=max| f(x)- g(x)|,当实际观测值D>D(n,α)则拒绝H0,否则则接受H0假设。
KS检验与t-检验之类的其他方法不同是KS检验不需要知道数据的分布情况,可以算是一种非参数检验方法。当然这样方便的代价就是当检验的数据分布符合特定的分布事,KS检验的灵敏度没有相应的检验来的高。在样本量比较小的时候,KS检验最为非参数检验在分析两组数据之间是否不同时相当常用。
PS:t-检验的假设是检验的数据满足正态分布,否则对于小样本不满足正态分布的数据用t-检验就会造成较大的偏差,虽然对于大样本不满足正态分布的数据而言t-检验还是相当精确有效的手段。
KS检验是如何工作的?
-
首先观察下分析数据
对于以下两组数据:
controlB={1.26, 0.34, 0.70, 1.75, 50.57, 1.55, 0.08, 0.42, 0.50, 3.20, 0.15, 0.49, 0.95, 0.24, 1.37, 0.17, 6.98, 0.10, 0.94, 0.38}
treatmentB= {2.37, 2.16, 14.82, 1.73, 41.04, 0.23, 1.32, 2.91, 39.41, 0.11, 27.44, 4.51, 0.51, 4.50, 0.18, 14.68, 4.66, 1.30, 2.06, 1.19}
对于controlB,这些数据的统计描述如下:
Mean = 3.61
Median = 0.60
High = 50.6 Low = 0.08
Standard Deviation = 11.2
可以发现这组数据并不符合正态分布, 否则大约有15%的数据会小于均值-标准差(3.61-11.2),而数据中显然没有小于0的数。 -
观察数据的累计分段函数(Cumulative Fraction Function)
对controlB数据从小到大进行排序:
sorted controlB={0.08, 0.10, 0.15, 0.17, 0.24, 0.34, 0.38, 0.42, 0.49, 0.50, 0.70, 0.94, 0.95, 1.26, 1.37, 1.55, 1.75, 3.20, 6.98, 50.57}。10%的数据(2/20)小于0.15,85%(17/20)的数据小于3。所以,对任何数x来说,其累计分段就是所有比x小的数在数据集中所占的比例。下图就是controlB数据集的累计分段图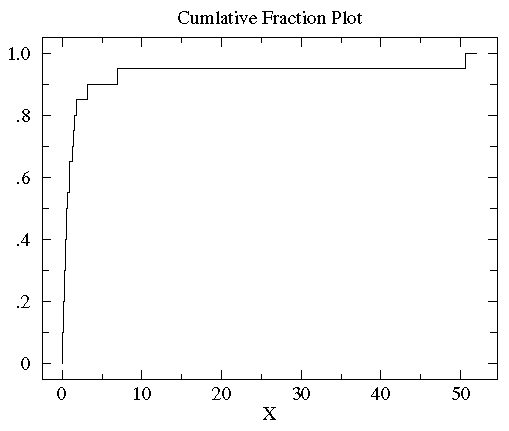
可以看到大多数数据都几种在图片左侧(数据值比较小),这就是非正态分布的标志。为了更好的观测数据在x轴上的分布,可以对x轴的坐标进行非等分的划分。在数据都为正的时候有一个很好的方法就是对x轴进行log转换。下图就是上图做log转换以后的图: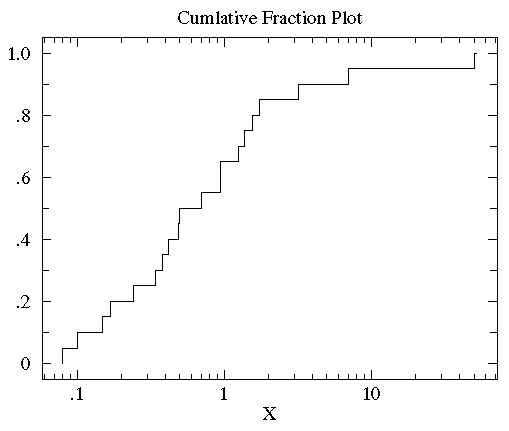
将treatmentB的数据也做相同的图(如下),可以发现treatmentB和controlB的数据分布范围大致相同(0.1 - 50)。但是对于大部分x值,在controlB数据集中比x小的数据所占的比例比在treatmentB中要高,也就是说达到相同累计比例的值在treatment组中比control中要高。KS检验使用的是两条累计分布曲线之间的最大垂直差作为D值(statistic D)作为描述两组数据之间的差异。在此图中这个D值出现在x=1附近,而D值为0.45(0.65-0.25)。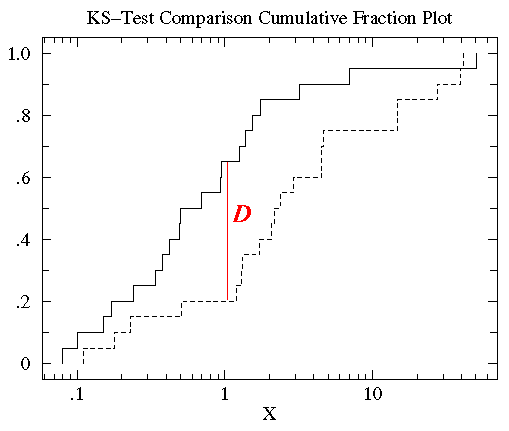
值得注意的是虽然累计分布曲线的性状会随着对数据做转换处理而改变(如log转换),但是D值的大小是不会变的。 -
百分比图(percentile plot)
估算分布函数肩形图(Estimated Distribution Function Ogive)是一种累计分段图的替代方式。其优势在于可以让你使用概率图纸作图(坐标轴经过特殊分段处理,y轴上的数值间隔符合正态分布),从而根据概率在y轴上的分布可以直观的判断数据到底有多符合正态分布,因为正态分布的数据在这种坐标上是呈一条直线。
那么这种图是如何画的呢?
假设我们有这5个数{-0.45, 1.11, 0.48, -0.82, -1.26},从小到大对它们进行排序,{ -1.26, -0.82, -0.45, 0.48, 1.11 }。0.45是中位数,百分比为0.5,而0.45的累计分布函数中占了0.4到0.6的区间。根据数据x在数据集(N)中排位r可以计算x的百分数(percentile)为r/(N+1)。将上述数据与他们的百分数配对,得到{ (-1.26,.167), (-0.82,.333), (-0.45,.5), (0.48,.667), (1.11,.833) }。然后将各点之间用直线连接就是百分比图了。如下图中红线所示(另一条线为累计分段曲线)。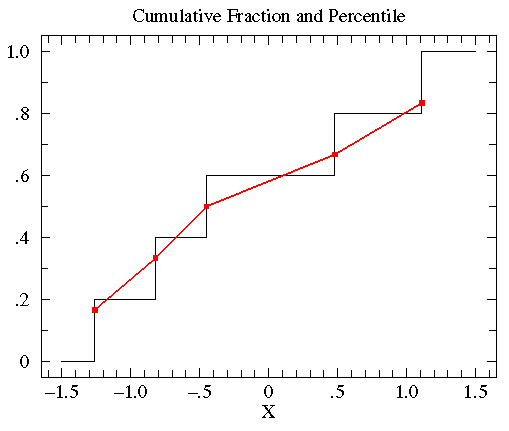
treatmentB的数据近似对数正态分布,其几何均值为2.563,标准差为6.795。该数据的百分图(红)与其近似的对数正态分布曲线(蓝)如下。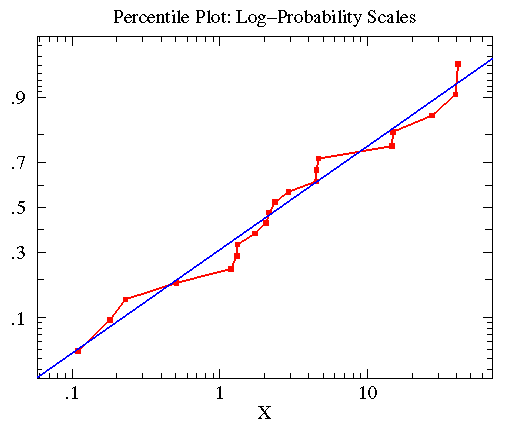
由于数据近似正态分布,所以对其采用t-检验是最佳的检验方法。
如何使用KS检验
在R中可以使用ks.test()函数。
与类似的分布检验方式比较
- 经常使用的拟合优度检验和Kolmogorov-Smirnov检验的检验功效较低,在许多计算机软件的Kolmogorov-Smirnov检验无论是大小样本都用大样本近似的公式,很不精准,一般使用Shapiro-Wilk检验和Lilliefor检验。
- Kolmogorov-Smirnov检验只能检验是否一个样本来自于一个已知样本,而Lilliefor检验可以检验是否来自未知总体。
- Shapiro-Wilk检验和Lilliefor检验都是进行大小排序后得到的,所以易受异常值的影响。
- Shapiro-Wilk检验只适用于小样本场合(3≤n≤50),其他方法的检验功效一般随样本容量的增大而增大。
- 拟合优度检验和Kolmogorov-Smirnov检验都采用实际频数和期望频数进行检验,前者既可用于连续总体,又可用于离散总体,而Kolmogorov-Smirnov检验只适用于连续和定量数据。
- 拟合优度检验的检验结果依赖于分组,而其他方法的检验结果与区间划分无关。



