PRML7-常数密度轮廓线

常数密度轮廓线(constant probability density contour)

对于PRML这本书中的图2.7，我不了解这张图表达的含义，于是谷歌到了这个名词。

在多元高斯分布中，对于某一常数\(c\)，满足下列公式的所有点\({\boldsymbol x}\)的集合组合成常数密度轮廓线：

\[(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})=c^2 \nonumber \\ ||\boldsymbol\Sigma^{-1/2}(\boldsymbol{x}-\boldsymbol{\mu})||=c^2 \]

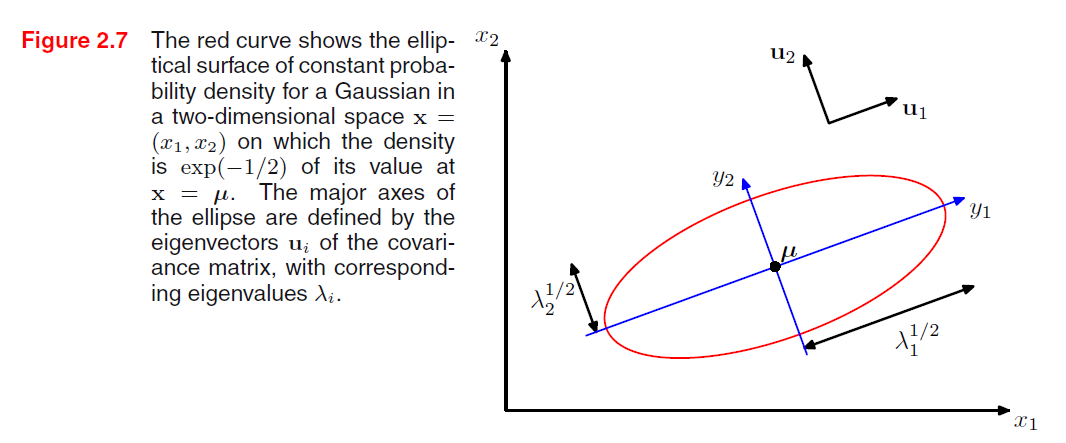
上图即为PRML书中图2.7，红色椭圆即为二维高斯分布中常数为exp(-1/2)存疑的常数密度轮廓线。取值为椭圆上的点的概率相同。但是对于椭圆内部的点，其概率要大于椭圆上的点（考虑z轴）。

这是以\(\boldsymbol \mu\)为中心，\(\pm c\sqrt{\lambda_j}\)为轴的椭球面，\(\lambda_j\)为协方差矩阵的其中一个特征值。

对于协方差矩阵\(\boldsymbol \Sigma\)进行特征分解，我们可以得到对角矩阵\(\boldsymbol\Lambda\)，正交矩阵\(\boldsymbol U\)，使得\(\boldsymbol \Sigma=\boldsymbol U\boldsymbol \Lambda\boldsymbol U^T\),而\(\boldsymbol U\)的第\(i\)列即为特征值\(\lambda_i\)的特征向量\(u_i\)。正交矩阵表示了坐标的旋转信息，对角矩阵则表示了坐标的放缩，所以说明了椭圆的轴平行于特征向量，半径大小正比于对应的特征值。

求解二维高斯分布

对于特征向量和特征值：

\[\begin{align} 0&=|\boldsymbol \Sigma-\lambda \boldsymbol I| \nonumber \\ 0&=\left|\begin{bmatrix} \sigma_1^2-\lambda & \rho \sigma_1\sigma_2\\ \rho \sigma_1\sigma_2 & \sigma_2^2-\lambda \end{bmatrix}\right| \nonumber \\ 0 &= (1-\rho^2)\sigma_1^2\sigma_2^2-\lambda(\sigma_1^2+\sigma_2^2)+\lambda^2 \nonumber \end{align} \]

根据一元二次求根公式可以求出：

\[\begin{align} \triangle &= \sqrt{(\sigma_1^2+\sigma_2^2)^2-4(1-\rho^2)\sigma_1^2\sigma_2^2} \nonumber \\ \lambda_1 &= \frac{1}{2}\left[(\sigma_1^2+\sigma_2^2)+\triangle\right]\nonumber \\ \lambda_2 &= \frac{1}{2}\left[(\sigma_1^2+\sigma_2^2)-\triangle\right] \nonumber \\ \end{align} \]

对于\(\lambda_1\)的特征向量：

\[u_2 = k_1u_1\nonumber \\ k_1 = \frac{\sigma_2^2-\sigma_1^2+2\lambda_1}{2\rho\sigma_1\sigma_2}\nonumber \\ \boldsymbol e_1=c_1\begin{bmatrix}1\\k_1 \end{bmatrix}\nonumber \]

又因为特征向量为正交矩阵，那么常数\(c_1\)为：

\[c_1 = \pm\frac{1}{\sqrt{1+k_1^2}} \]

同理可得\(\lambda_2\)的特征向量为：

\[\boldsymbol e_2 = c_2\begin{bmatrix}1\\k_2\end{bmatrix}\nonumber \\k_2 =\frac{\sigma_2^2-\sigma_1^2-2\lambda_1}{2\rho\sigma_1\sigma_2}\nonumber \\ c_2=\pm\frac{1}{\sqrt{1+k_2^2}}\nonumber \]

这样既满足特征向量为正交向量，也满足两个特征值的特征向量正交(\(\boldsymbol e_1^T\boldsymbol e_2=0\))。

当$\sigma_1=\sigma_2 $时，可以取特征向量：

\[\boldsymbol e_1=\begin{bmatrix}1\\1\end{bmatrix} ,\ \ \ \ \boldsymbol e_2=\begin{bmatrix}1\\-1\end{bmatrix} \]

根据之前的知识可以知道，只要相关系数\(\rho>0\)，那么椭圆会呈\(45^\circ\)倾斜，其数值大小不重要了。相反，若相关系数小于零，那么椭圆的主轴会垂直于\(45^\circ\)线。

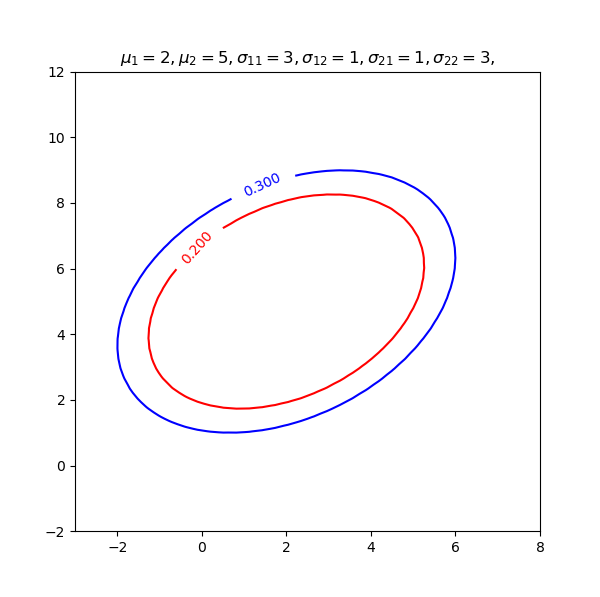
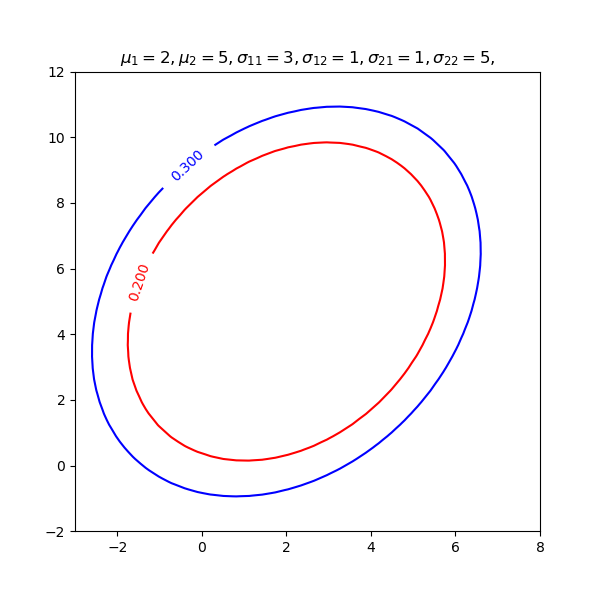
画图代码如下，虽然只有短短几行，却让我查了好久的资料。

import numpy as np
sampleNum = 50
x = np.linspace(-5, 10, sampleNum)
y = np.linspace(-5, 12, sampleNum)
x, y = np.meshgrid(x, y)
mean = np.array([2,5])
cov = np.array([[3,1],[1,5]])
data = [i for i in zip(x.flat, y.flat)]
z = np.array([])
a = 2*np.pi*np.sqrt(np.linalg.det(cov))
c = np.linalg.inv(cov)
for i in data:
    b = np.array(i)-mean
    z = np.append(z, 1/a*np.dot(np.dot(b, c), b.T))

import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
m= plt.tricontour(x.ravel(),y.ravel(),z.ravel(),[0.2,0.3], colors = ('r','b'))
plt.clabel(m, colors = ('r','b'))
plt.title(r'$\mu_1 = 2, \mu_2 = 5, \sigma_{11}=3,\sigma_{12}=1,\sigma_{21}=1,\sigma_{22}=5,$')
plt.xlim(-3, 8)
plt.ylim(-2,12)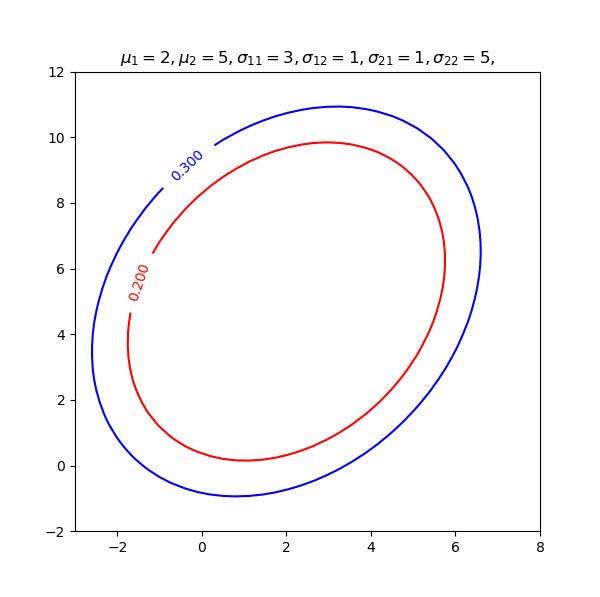![](https://img2018.cnblogs.com/blog/1012967/202002/1012967-20200216191617898-1598349157.png)

plt.show()

参考

pyplot的contour函数

python matplotlib contour画等高线图