2024.11
P10099 [ROIR 2023 Day 2] 美丽序列
枚举当前点放哪个数,上一个
距离的取值只有
P2993 [FJOI2014] 最短路径树问题
建出最短路图(若
从
这样为什么是对的?
对于两条到
若
后面是点分治板子。submission
P3164 [CQOI2014] 和谐矩阵
不难列出
如果矩阵满秩,一定无解,因为最终可以消成
否则把任意一个自由元设为
P9905 [COCI 2023/2024 #1] AN2DL
二维单调队列板子。
P4796 [BalticOI 2018] 路径
P3165 [CQOI2014] 排序机械臂
平衡树裸题:1. 区间翻转 2. 单点删除 3. 查询子树最小值。
P3172 [CQOI2015] 选数
设
选出
整除分块,杜教筛求
$1:杜教筛
记
移项:
$2:一个精妙的容斥
对于
记
设
所求即
P4792 [BalticOI 2018] 火星人的 DNA
双指针板子。下位黄,哪来蓝的。
P10100 [ROIR 2023 Day 2] 石头
对于询问
不妨考虑第一种。
假设起始点为
我们需要循环往复执行一下操作:左移
称
说的形象一点,设左边的阈值下标集合为
左侧最大阈值必须小于
也就是说,
左边最大阈值必须大于右边除
否则左边比右边先走完。
现在找到了判断某个
如果
否则只需考虑
从右往左枚举
P10101 [ROIR 2023 Day 2] 一个普通的字符串问题
题意:求长度为
所求
枚举起点终点,终点向起点连边,转化为BEST定理求欧拉回路,最后除以每条重边的阶乘。
(新加的边是和原来重边区分的)
QOJ 5981
原问题转化为,求最小的花费,确定
如果
这启发我们进行区间DP,
为什么要取max?因为我们考虑的是最坏情况,
答案很小,容易构造出一个上界
交换值域定义域,
考虑在
因此
树状数组优化转移,细节较多,且时空复杂度很劣,过不了原题。
$正解
把上面朴素方程的
初始化
设
枚举
令 <-- 表示更新。
上述转移只能更新到边界,因此还需
最多访问到
沙漠点列(link)
题意:给出一个沙漠,删去其中的
如果存在割边,则删割边。
否则需要断环来创造割边,断开一个长度为
tarjan找环,贪心的按环长排序。
QOJ 5173
肯定是单方向从
显然有染色上界
如果某个
推广一下,如果存在
问题转化为,选出最多的二元组
假设当前在
问题转化为,从
据说倍增卡常,对
并查集必须按秩合并路径压缩都加上复杂度才是
QOJ 7855
点分树维护路径问题。
对于每一个分治中心,只有最小和次小的两个
如果
对每个分治中心维护一个大小为
如何修改?点分树将包含
全局答案如果用可删堆维护会多一个log,同样指针维护,因为答案是不降的。
时空复杂度
P5921 [POI1999] 原始生物
一个自然的想法是连边
问题转化为:添加最少的边,使得原图存在一条欧拉路径。
独立考虑每个弱连通分量,显然
如果
如果
接下来同理,新增边数为
P5944 [POI2002] 出圈游戏
稍微转化一下就是
excrt 板子,难点在于唐氏题面。
P3426 [POI2005] SZA-Template
记前缀
显然
-
设
-
对于
border 的 border 还是 border,因此
令
根据上述两个推论,要么
证明:
P5913 [POI2004] KAG
每个连通块只能通过第一类操作合并为原图,单独考虑每个连通块。
注意到,第二类操作等价于补图意义下的第一类操作。
- 依次检查原图每个极大连通块。
- 建出补图,依次检查每个连通块的补图。
交替执行上述操作,若最终能被拆分为若干单点,则原图是
操作一是
每次操作二至少消耗
优化操作二,如何找到
链表维护当前未被拓展的点,对应当前点枚举所有未被拓展的点。
如果他们没有边相连,说明他们在补图上连通,把他加入队列并从链表中删除。
每个点只会拓展一次,而"有边相连"的情况只会发生
总复杂度
P3429 [POI2005] DWA-Two Parties
假设答案为
高斯消元
现在证明该方程组一定有解。
无解当且仅当从中选出若干方程,他们异或起来满足左边各项系数为
第
-
有奇数个奇度点被选,这保证了右边为
-
每个被选奇度点,有奇数个相邻点被选;其他所有点(不一定被选)有偶数个相邻点被选。
选
构造一个新图,满足点集仍是原图点集,边集为
新图中,
奇数个奇度点度数仍是奇数,这与无向图度数和为偶数矛盾,故
P5919 [POI2004] MAK
不难得到一个置换的
问题转化为,求一组正整数
如果已知
对于一个环
其能产生的最小字典序为
一个环所占值域一定是一段连续区间。
贪心的将长度小的环放在前面,从
-
如果
贪心的将自环放在最开头,显然自环多的字典序小。
-
一定存在一组最优方案,使得所有环长两两互质。
假设
-
一定存在一组最优方案,使得所有环长都是质数幂次。
假如
显然将
证明就是对于大于
考虑筛出
较大的质数基本用不到,实测取前
由于只要比对大小,我们不妨将 double 下比较。
如果最优方案的总和不满
P6756 [BalticOI2013] Brunhilda’s Birthday
记
考虑填表法,
下面说明
假设
如果
否则
设
P9179 [COCI2022-2023#5] Logaritam
对于
一个数改动,说明其至少有一个质因子发生改动。
一个质数改动,只会改动其所有倍数,且不产生矛盾,贪心的选最大指数即可。
P9180 [COCI2022-2023#5] Slastičarnica
在钦定当前左端点位置,满足了几个要求下,显然右端点越远越好。
设
设
同理
以上信息容易
考虑第
P2048 [NOI2010] 超级钢琴
通过某种方式找到前
设
容易st表预处理后
假设当前全局最大值为
优先队列维护一个bfs状物即可。
NFLSOJ 12394
题意:给定
求最长好子序列的长度,
注意到,
找到第一个
对于
综上所述,每次最多改动一个位置,且这个位置唯一确定,时间复杂度
P3226 [HNOI2012] 集合选数
构造一个矩阵:
1 2 4 8 16 32 ...
3 6 12 24 48 96 ...
9 18 36 72 ...
27 ...
设左上角元素为
问题转化为,在这个矩阵中,选出一个集合,满足没有相邻的两个元素被同时选中的方案数。
行列都只有
然而光是这一个矩阵不能覆盖所有
根据乘法原理,每个矩阵的结果相乘即可。
NFLSOJ 971
题意:构造一颗恰有
限制:
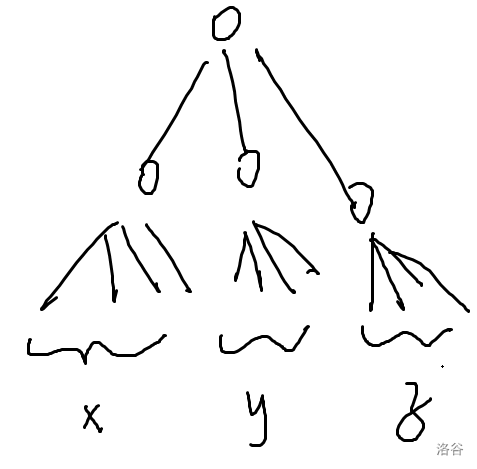
这样就花费
类似的,可以构造出一棵
打表验证,上面两种已经覆盖了全部情况。
P6869 [COCI2019-2020#5] Putovanje
统计每条边遍历次数,树上差分解决。
P6742 [BalticOI 2014 Day2] Portals
自己手玩一下,存在一种最优方案使得两个传送门是从同一点发射的。
肯定是挑离自己最近的一个墙壁发射一个,然后传送到另一个方向的墙壁。
预处理每个点到四个方向墙壁中的最短距离,然后跑最短路即可。
HDU 6883
题意:给定
选出一个物品必须先选其上方所有物品,
给定
每个堆对答案的贡献只有四种:不选,
把一个堆拆为两个互相独立的物品:体积
决策新物品选或不选就能覆盖原问题的全部情况。
贪心的按
如果某个前缀的体积和恰好为
否则这个前缀恰好比
两种调整办法:在已选物品中找到体积为
排序部分如果桶排可以做到
P7913 [CSP-S 2021] 廊桥分配
一眼三分,然后假了,因为存在一段连续的函数值相同。
假设一开始有无限多个廊桥:
按照时间顺序给每个飞机分配当前可用编号最小的廊桥,设
如果限制廊桥个数只有
处理一个前缀和数组然后枚举
P7915 [CSP-S 2021] 回文
根据第一步的决策进行分类讨论,假设第一步选 L。
找到和
问题转换为:给你两个栈
还是考虑第一步,如果要弹出
在
把栈顶和对应栈底都弹出后,变为了一个规模为
P7914 [CSP-S 2021] 括号序列
基本独立想出来的(因为用了std调试)。
()、(S)是好的,S表示仅由不超过*组成的非空字符串。- 如果
A和B是好的,那么AB、ASB是好的。 - 如果
A是好的,那么(A)、(SA)、(AS)是好的。
设 S 串。
设 A 或 S 或 SA 或 AS 的方案数。
考虑如何计算
如果
对于某个固定的
那么:
后面那个用后缀和优化下就能变成
P7960 [NOIP2021] 报数
小常数 1e7 单 log 是能冲过 1s 的。
P7961 [NOIP2021] 数列
设
往后转移,决策放了
复杂度
P7962 [NOIP2021] 方差
假设现在有四个数
变换前后差分数组分别为
不难发现,该操作等价于交换差分。
感性理解一下,存在一组最优解使得差分数组是单谷的,因为这样能使数组尽可能平均。
将差分数组排序,从小到大插入,每次插在前面或后面。
化简答案:
直接维护两个东西的差不是很好做,考虑把一维记在状态里。
转移考虑每个
差分为
时间复杂度
CF2035B
题意:构造一个长度为
不会出现
P3561 [POI2017] Turysta
【参考】:竞赛图性质研究。
结论1:竞赛图强连通缩点后的DAG呈链状,且前面的所有点向后面的所有点连边。
归纳证明,逐个加入强连通分量。
设橙色点为当前加入的 scc:如果
否则
结论2:任意竞赛图存在一条哈密顿链。
增量构造,考虑在当前链的基础上加入点
如果
否则,用
一定存在相邻的
时间复杂度
结论3:强连通的竞赛图一定存在哈密顿圈。
假设已经找出了一条链。
找到指向链头的一个点
一定存在这么一个
考虑加入
如果
否则找到第一个
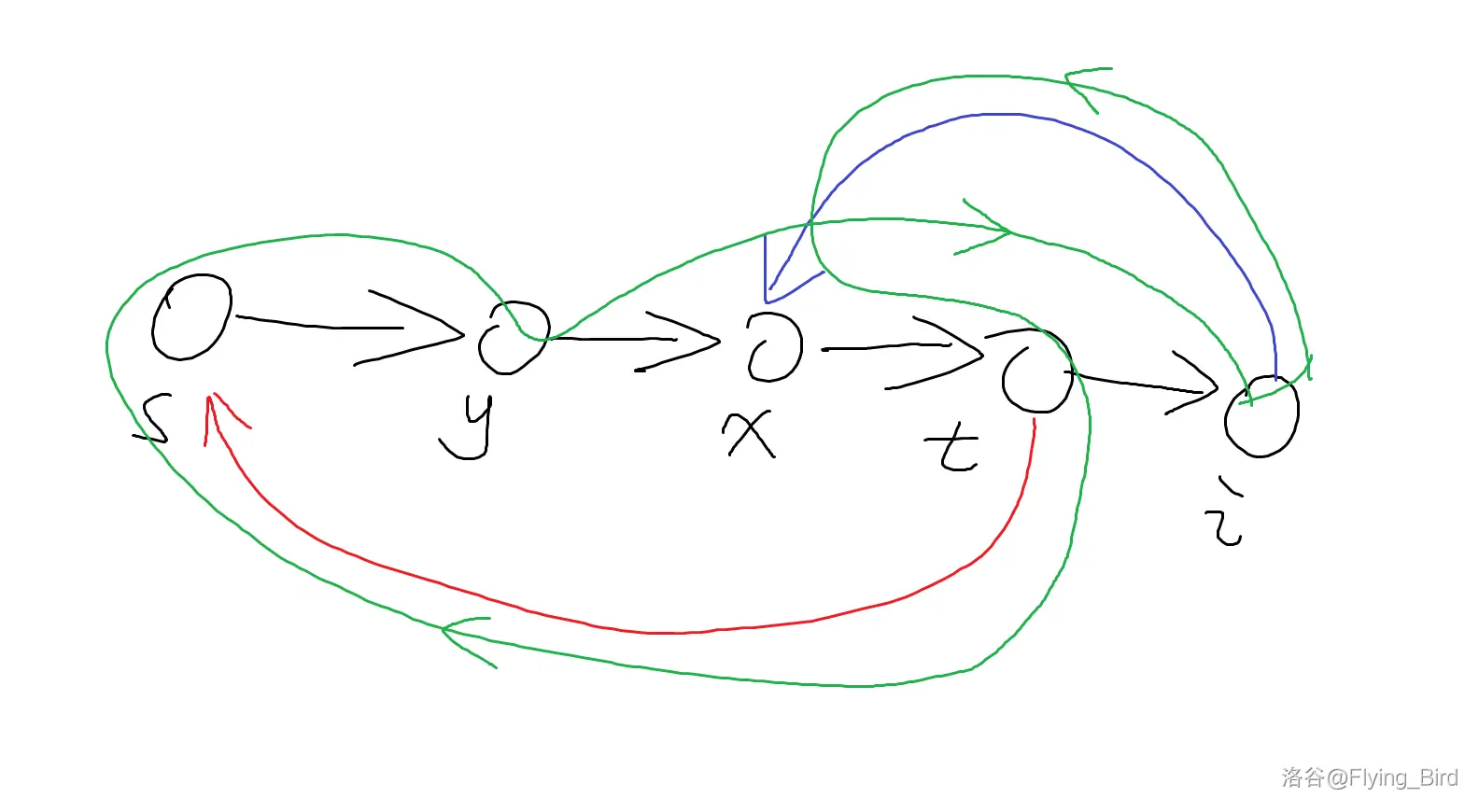
即设
因为
如果找不到
不妨先跳过当前点继续往下走,直到找到一个
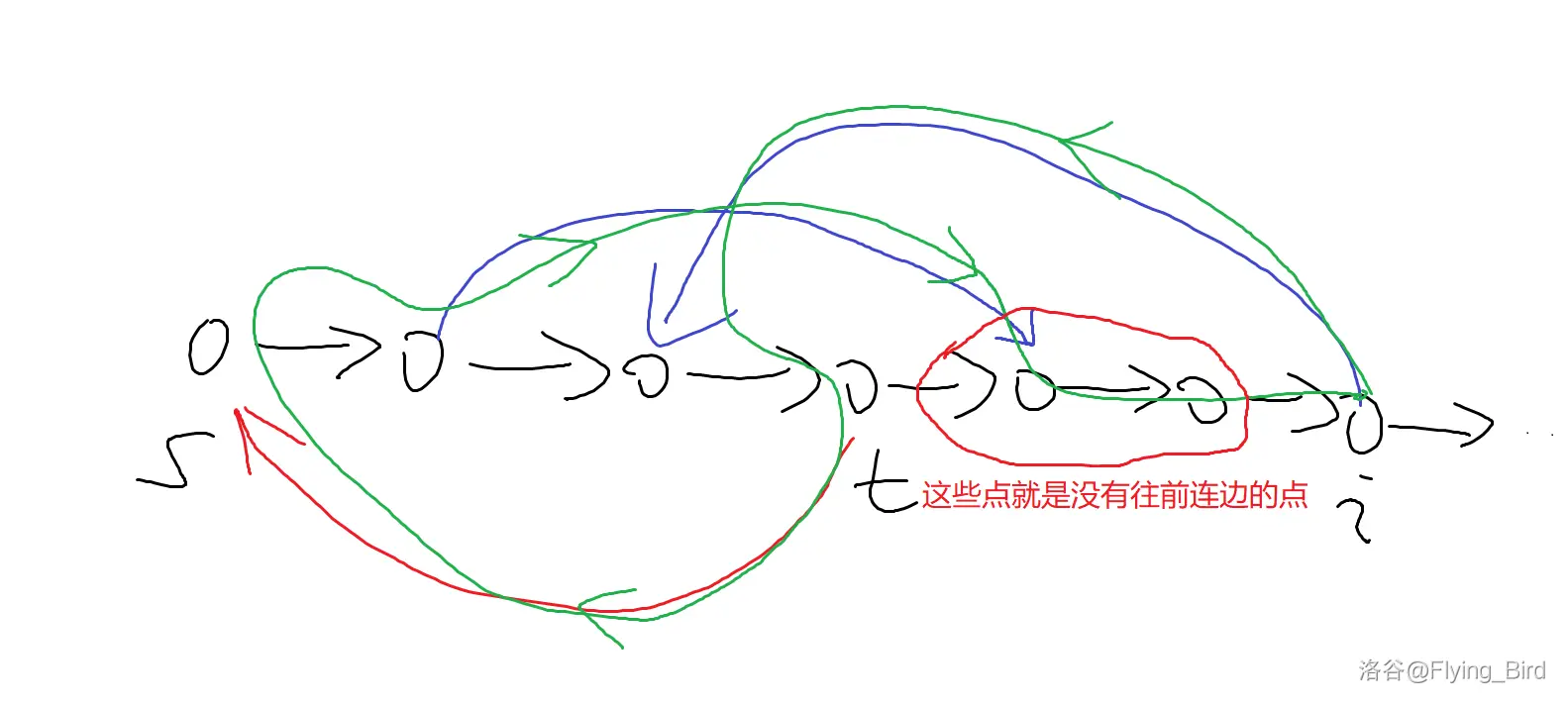
即:
同时更新
本题做法:
缩点,对于每个强连通分量跑出哈密顿回路。
对于每组询问,从
CF1685C
用
一个重要的观察:答案不超过
设
对于
答案为零容易判断,现在只要考虑答案是否为
假设翻转
设
那么
贪心的选
**マス目と整数 **(link)
前面忘了,黑降绿,后面忘了。
a b
c d
e f
推广到相邻两列差值相同,等价于任意两列差值相同(相同行元素)。这是条件成立的充要条件。
如果同时存在
带权并查集判断是否出现矛盾。
否则所有列的差值关系都被确定,接下来考虑点权非负的限制。
对于每个连通块,选出基准列
以该基准列出发,跑出该连通块其他权值,看是否非负即可。
CF883D
二分答案
设
如果
如果
如果某个
因此如果
时间复杂度
P11290 【MX-S6-T2】「KDOI-11」飞船
设当前速度为
当
二分出终点前第一个加油站位置并统计答案即可。
CF461E
如果
注意到
因此
有如下贪心:对于每一段,能延伸就延伸(在
在段数相同的情况下要最小化总长度,这样才能在总长度确定时最大化段数。
设
倍增优化:
问题转化为求
其代表的子串在将来一定是接一个
把以
- 是
- 是
- 不是
因此在相同长度下,一三比二更优。
固定长度为
存在一三串当且仅当
对所有后缀建出树高为
统计答案:从高到低枚举
由于有“不能接”这一限制,贪心的让
P9195 [JOI Open 2016] JOIRIS
如果所有
在模
存在一种构造,是一个长度为
设
在
从左往右做一遍,这样可以使
P9350 [JOI 2023 Final] Advertisement 2
把
这两种情况又能统一为
这是一个二维偏序问题,
按照横纵标排序,跑一个纵坐标的单调栈即可。
P3557 [POI2013] GRA-Tower Defense Game
称距离为
证明以下策略是正确的:随便找到一个未被染色的点并往外拓展。
设原图一个大小为
从
每次至少会走到一个新的
- 和
- 存在
因此
CF1592D
由于
如何让询问的点集连通?
可以在长度为
询问次数为
NFLSOJ 10305
题意:给定无向图
- 不存在
其中
数据范围:
小数完全没用,因为不等号两边可以同时乘
设边权
- 一条正权边。
- 一个边权和为正的环。
- 一个边权和大于
显然如果第二种情况存在,必然第一种情况存在,因此只需判断有无正权边。
现在所有边为负,要找一个边权和最大的奇环。
拆点,设
对每个
当且仅当 d[x] + w > d[y] 才松弛可以使最长路上的点不重复。
但是没有保证原图上的点也不重复,即可能出现同一个点的奇点偶点同时出现在路径中的情况。
取这两个点之间的一段作为新环,边数为奇,且总和一定大于
AT_code_festival_2017_qualc_f
设
假设已经知道
从后往前考虑。
即这三个数在
再考虑倒数第二步,同样只要满足
不会对第
此时
因此操作序列确定时,
问题转化为有多少合法的
当
合法当且仅当对于任意
计算系数时,已经保证了
现在只要保证
考虑
上下两部分无交,元素总数为
为什么要从后往前考虑?因为如果从前往后,不能取的上下两部分有交,不容易计算。
因此合法
设计一个DP:
前缀和优化一下就能
[ARC172D] Distance Ranking
记
构造
现在考虑
注意第二项展开后有
P5361 [SDOI2019] 热闹的聚会与尴尬的聚会
题意:找一个导出子图,设其最小度数为
需要满足:
分析一下这个奇怪的条件:
即不管整不整除,两个限制都等价于
最大化
最大化
考虑如下策略:每次选度数最小的点,并删除他和他的邻域。
被选点度数一定不超过
因此每选一个点,最多新删除
一直选点直到所有点被删除,有
P6982 [NEERC2015] Jump
题意:每次询问一个 01 串
在不超过
考虑
在这
证明:
现在已经得到了一个交集为
设
对
固定
枚举
这样我们就得到了一个最坏询问次数为
考虑随机来得到第一步:一次正确的概率为
QOJ 7864. Random Tree Parking
题意:给定一棵树,求长度为
枚举
数据范围:
注意到如下事实:一个合法的
考虑进行子树 DP,统计
把所有属于
设
我们可以知道
现在考虑合并
现在往子节点组成的序列中插入
最后
由于整棵树随机,树高期望
QOJ 8049. Equal Sums
朴素 DP:
前缀和优化可以做到
考虑状态
这样就把第三维控制在了
QOJ 9479. And DNA
题意:计数序列
数据范围:
逐位考虑,
在最低位时,满足对于所有
我们发现,只有全
由于进位是统一的,这说明在更高位
设
设
-
-
唯一问题只剩
考虑对序列
如果这个
如果组成
有递推式
DP 过程中有没有可能出现
AT_joi2020ho_c
断环成链,
P9743 「KDOI-06-J」旅行
- 从上面走下来:
- 从左边走过来:
- 原地买一张往下的票:
- 原地买一张往右的票:
如果一个方案满足两类票在
因此最后还要减去
时间复杂度
P9034 「KDOI-04」Again Counting Set
题意:对可重集
对于第三条限制:要么
如果全
现在设
感性理解一下
- 满足
P11323 【MX-S7-T1】「SMOI-R2」Happy Card
优先花三带一最优。把炸弹看成三带自己。
每种牌尽可能多的分成
一张
一张
因此先用
一张或两张
按照平均花费,一定是四张四张花最优,最后再处理余数。
贪心,太困难了!
P11324 【MX-S7-T2】「SMOI-R2」Speaker
题意:每次给出
设
设
问题转化为查询
P10217 [省选联考 2024] 季风
首先有
我们想让
得到条件成立的一个必要条件:
随便构造一组
此时
调整
把绝对值拆成四个不等式,一个
枚举
分别解四个不等式可以得到合法
P9755 [CSP-S 2023] 种树
二分答案,设
如果没被种,把他到根的一条链都种上(其他位置
[ARC188A] ABC Symmetry
首先解决判定问题,一个串合法当且仅当 A B C 出现次数的奇偶性相同。
设 AC 的个数为偶,B 个数为奇的前缀个数。
不难设计一个朴素状态
因此不妨将互补的状态合并,
一种更巧妙的方式是 ABC 分别看作 123,
AT_joi2019ho_b
画框从小到大排序,画按美丽度从小到大排序。
第
选取能放进第
AT_s8pc_5_e
题意:给定一张包含 #.G 的网格,G 为终点,# 为石砖,. 为冰砖。
冰砖不能转向,石砖能转向。每经过一个石砖走一步的代价增加
对于所有起点,求出他们到 G 的最短路,
把所有石砖和终点拉出来建图,总边数
设 G 的最短路,从大到小 DP。
由于最多经过
对于每个冰砖
AT_s8pc_5_f
换种表达描述贡献:从大到小遍历
否则
一旦一个
当前清算完的区间是没有后效性的,这启发我们使用区间 DP:
如果
否则根据
其中
时间复杂度
P9871 [NOIP2023] 天天爱打卡
把
设
其中
考虑扫描线,在右端点处加入每个线段,设
经典把
线段树维护
每加入一个线段
注意到一个线段右端点到下一个右端点之间的
而对于转移用的断点,其一定是某个左端点减一,否则不优。
这启发我们把所有右端点和左端点减一离散化,时间复杂度优化至
P9754 [CSP-S 2023] 结构体
完全不需要考虑复杂度,直接模拟。
P9119 [春季测试 2023] 圣诞树
对于这种产生交点的情况,走
存在一种最优方案使得路径无交。
因此我们从
断环成链,跑区间 DP 即可。
P8817 [CSP-S 2022] 假期计划
枚举 B, C,枚举 B 能到达且 1 也能到达的点作为 A,同样枚举 D。
贪心的取 A 为符合条件的点中价值最大的,但可能出现 A 和 C, D 相等的情况。
枚举 A 为符合条件的点中最大的前三个,这样一定能遍历到最优解,且枚举量降为
P8867 [NOIP2022] 建造军营
边双缩点成一棵树,所有树边都是原图割边。
如果两个边双内部都有点被选,那么其在新树上的路径必须全部被选。
设
设
那么
钦定
本质在被选点集形成的虚树沿着被选边往上延伸到到的最高点
另一种更自然的统计方法是枚举点集的 LCA(虚树的根),但是转移方程不如上述方法简洁。
P5664 [CSP-S2019] Emiya 家今天的饭
- 被选点集非空。
- 每一行至多选一个点。
- 设选出的总点数为
如果只有前两条限制,那么总方案为
现在考虑容斥减掉符合前两条但不符合第三条的方案。
注意到
枚举这个非法的列,设
将
转化一下条件,非法当且仅当
[ARC104D] Multiset Mean
P11268 【MX-S5-T2】买东西题
[ARC136E] Non-coprime DAG
[ABC163E] Active Infants
[ARC107D] Number of Multisets
P4778 Counting swaps




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 25岁的心里话
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· 零经验选手,Compose 一天开发一款小游戏!
· 因为Apifox不支持离线,我果断选择了Apipost!
· 通过 API 将Deepseek响应流式内容输出到前端