CSP2024-38
2A
题意:定义 \(S(n, k)\) 为 \(n\) 在 \(k\) 进制下的数位和。
给定 \(n, k, x\),求 \(\sum_{i = 2}^k[S(n, i) \le x]\)。\(n \le 10^{12},\ k, x \le 10^{18}\)。
-
\(i \le \sqrt n\),直接枚举。
-
\(i > \sqrt n\),最多两位数,总和等于 \(\lfloor\dfrac{n}{i}\rfloor + (n\bmod i) = n - (i - 1) \lfloor\dfrac{n}{i}\rfloor\)。
枚举 \(\lfloor\dfrac{n}{i}\rfloor\),算合法范围即可。
时间复杂度 \(O(n\sqrt n)\)。submission
A
题意:\(n\times m\) 的网格,每个位置可以水平和垂直方向各连一条边。
当且仅当两个位置互相连边会产生价值 \(a_i \oplus a_j + \text{popcount}(a_i \oplus a_j)\),问最大价值和。
不难发现每行每列都是独立的,分别做线性 DP 即可。
B
题意:维护长度为 \(n\) 的序列,每次全局加减一个数,对 \(0\) 取 \(\max\),\(a_i\) 对 \(i\) 取 \(\max\),求全局和。
数据范围:\(n\le 10^9,q \le 10^6\)。
(由于题解图画太好了,所以全部贺过来了)
初始状态,高度代表容量。
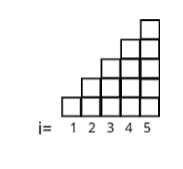
初始 \(l, r\) 指针汇聚在 \(0\),加水对应 \(r\) 上升,减水对应 \(l\) 上升。

此时如果再加水可以发现是从最底层开始加的,即新增指针 \(l_1 = 1,\ r_2 = d\)。

如果 \(r\) 与上次层的 \(l\) 相遇,则两部分合并,并向上溢出。
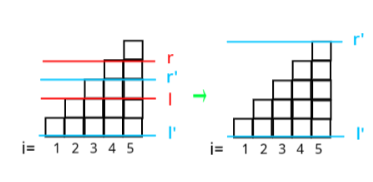
此时再减水是从下往上考虑每个区间,上移 \(l\) 直到 \(l, r\) 相遇,该区间消失。
栈维护所有区间,栈顶存储最底下的元素,时间复杂度 \(O(q)\)。
C
题意:长度为 \(n\) 的序列,初始将 \(m\) 段区间染成黑色(可以重复染色)。
一次操作定义为将长度为 \(x\) 的区间染成黑色,求至多 \(k\) 次操作后最长连续黑色区间长度。
数据范围:\(1\le, k, x\le n\le 10^9,\ 1\le m \le 10^5\)。
首先可以一边扫描将有交区间全部合并。
如果答案区间不包含原区间:贡献为 \(\max(n, k\times x)\)。
否则枚举其包含的最左侧的原区间:
左边的决策:一直放 \([l- x,\ l - 1]\),\(l\) 表示当前左端点(\(l - x < 1\) 时可能向右偏移部分,此时产生负贡献)。
右边的决策:一直放 \([r + 1, r + x]\),如果 \(r\) 被包含在某个原有区间 \([l_0, r_0]\),直接跳到 \(r_0 + 1\),产生正贡献。
这里的正负贡献都是相对于 “不考虑原区间,直接放” 而言的。
显然是要让正贡献越多越好,即往右边跳越多个原区间。
对于某个线段 \([l_0, r_0]\),显然是一直跳与 \(r_0 + 1\) 在模 \(x\) 意义下同余的位置,直到被某个右侧线段覆盖。
这可以从后往前线段树维护区间覆盖得到(当然可以颜色均摊段)。
考虑倍增,找到最多能在 \(k\) 限制下跳多少个线段,然后利用剩余步数往左右延伸即可。


