题意:将一个圆等分为 分,给出其中 个等分点的编号,。
有向边 存在,当且仅当 是距离 最大的点(不唯一),且与图中其他边无交点(端点不算)。
求图中最多有多少条边。。
引理:不存在 ,其中 互不相同。
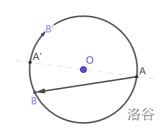
作过 的直径 ,作 关于 的对称点
- 如果 或 在 上,由于大弧对大角 , 的边不能存在,矛盾。
- 如果 包含于 ,,矛盾。
- 如果 在 , 在 ,两边相交,不合法。
因此合法的状态只有两种:以某个点为中心的菊花状图;三条边首尾相连形成的等腰三角形。
注意两点的距离可以由对应弧长表示,也可以表示为跨过了多少整段:,这是个凸函数,可以二分找分界点。
求出离每个 距离最大的点集(最多两个),时间复杂度 。(双指针能做到线性)
submission
题意:给出字符串 ,文本串 的权值定义为 作为子序列在 出现的次数乘上 作为子序列在 出现的此次数。
给定 ,求 所有子串的权值和。。
考虑没对子序列 对答案的贡献(被多少区间包含),显然是第一个出现的位置乘上从最后位置开始的一个后缀长度。
设 表示前 个字符,匹配到 的第 位, 的第 位的开头位置和。
考虑以 结尾的贡献,不能从第五种转移过来(因为对应方案 不是结尾),前四种转移过后的 乘上 。
submission
定义函数:
给定长度为 的数组 ,定义一段区间 的优美度等于:
次询问,每次给出 和参数 ,求 的最大优美度,以及对应最小的 。
数据范围:。
交换一下求和号:
注意到 ,其中 表示 的所有正因子和。
那么所求为:
记 :
注意到 是关于 的一次函数,且斜率和截距均容易计算。
我们将询问离线,从前往后插入直线,问题转化横坐标为 时 的最大值(及编号),李超线段树维护。
submission(你说得对但是我不会线性筛 sigma)




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步