训练记录（Jul.）

杂题

CF1778F *2600/省选/NOI-

CF1167E *2100/提高+/省选-

CF156C *2000/普及+/提高

结论：和相同的任意一种状态都能到达。

证明：看做 $n$ 堆硬币，每堆任何时候不超过 $25$，始终存在一种方式移动一枚硬币到其他地方。

等价于求 $x_1 + x_2 + \cdots + x_n = \sum a_i \quad (x_i \in [1, 26])$ 的解的数量。

法一：$f_{i, s}$ 表示前 $i$ 个数，和为 $s$ 的方案数，$f_{i, s} = \sum f_{i - 1, s - x_i}$。

法二：容斥，钦定一些位置大于 $26$，$\sum\limits_{i = 0}^n (-1)^i \begin{pmatrix} n\\i\end{pmatrix} \begin{pmatrix} s - 26i - 1\\n - 1\end{pmatrix}$。

法三：生成函数暴力草。

CF622C *1700/普及+/提高

线段树查询 $[l, r]$ 最小/最大值下标，学数据结构学的。

更简单的做法：$lst_i$ 表示上一个与 $a_i$ 不同的数的下标，$a_r \ne x$ 直接输出；$a_r = x$ 且 $lst_i < l$ 无解；$a_r = x$ 且 $lst_i \ge l$，输出 $lst_i$。

CF671A *1800/普及+/提高

需要决策的只有第一步，如果两个人的最优决策互不干扰，直接选就是了，否则讨论以下次优决策。

有可能出现一个人压根没走的情况。

CF597C *1900/普及+/提高

$f_{i, j}$ 表示以 $a_i$ 结尾长度为 $j$ 的序列个数，随便写个 bit 优化即可，这也配绿？

CF1840D *1400

最大值最小，二分答案。首先对 $a$ 排序，选的点一定在 $a_1 \sim a_n$ 之间，否则不优。

设当前答案为 $d$，选一个点能覆盖 $2d$ 的区间，看最后点数是否 $\le3$。

CF1833G *1800

很直白的题，叶子的删边方式是唯一的，自下而上模拟即可。

CF476D *1900

所有数都除 $k$ 后即找 $n$ 个两两互素的四元组，且最大值最小。

一个四元组内只能有一个偶数 $e$，也就是必须消耗 $3$ 个奇数。

不妨猜想每个组都形如 $\{e - 1,\ e,\ e + 1,\ e + 3\}$，证明他们两两互素。

$e + 1 \not\perp e + 3$。

如果存在 $d > 1$ 使得 $d \mid e + 1$ 且 $d \mid e + 3$，则 $d \mid (e + 3) - (e + 1)$，矛盾。

同理可证 $e - 1 \not\perp e + 3$ 和 $e \not\perp e + 3$。

KMP

几个定义：

$pre_i = s[1, i]$，$suf_i = s[n - i + 1, n]$。
$p$ 是 $s$ 的 border 当且仅当 $pre_p = suf_p$，特殊的，$n$ 一定是 $s$ 的 border。
$p$ 是 $s$ 的周期当且仅当 $\forall i > p,\ s_i = s_{i - p}$，特殊的，$n$ 一定是 $s$ 的周期。
周期 $p$ 是 $s$ 的 循环节 当且仅当 $p \mid n$，特殊的，$n$ 一定是 $s$ 的循环节。

定理1：$p$ 是 $s$ 的周期等价于 $n - p$ 是 $s$ 的 border。

证明：$q$ 是 $s$ 的 border：$s_1 = s_{n - q + 1}, \cdots, s_q = s_n$。不难得到 $n - q$ 是 $s$ 的周期。

注意：border 没有二分性。

border 的暴力求法：枚举 $1 \le i \le n$，检验是否有 $pre_i = suf_i$，时间复杂度 $O(n^2)$。

优雅的暴力：哈希 $O(1)$ 判定前后缀相等。缺点：常数大，会被卡。

定理2：$s$ 的 border 的 border 也是 $s$ 的 border。

证明：画个图很好理解。

推论：求 $s$ 的所有 border 等价于求所有前缀的最大 border。

$p = n$ 是 $s$ 的最大 border，然后我们要求 $p$ 的最大（不为本身） border，化归为子问题。

Next 数组

定义：$ne_i$ 表示 $pre_i$ 的最大非平凡 border，其中 $ne_1 = 0$。

不难发现 $pre_i$ 的所有 border 减 $1$ 一定是是 $pre_{i - 1}$ 的 border。

因此我们依次检查 $ne_{i - 1}, ne_{ne_{i - 1}}\cdots$ （即 $pre_{i - 1}$ 的所有 border）的下一位是否等于 $s_i$，以此递推出 $ne_i$。

时间复杂度分析：

如果 $ne_i = ne_{i - 1} + 1$，势能（最大迭代次数）增加 $1$，
否则会先迭代到某个 $ne_j$，然后 $ne_i = ne_j + 1$，势能不增。
否则 $ne_i = 0$，势能清空。

综上，势能总量为 $O(n)$，时间复杂度 $O(n)$，常数大概在 $2$ 左右。

P3375 【模板】KMP：0-base，1-base

NC15165

对于 $s$，求最长的子串 $t$，满足：$t$ 是 $s$ 的前缀；$t$ 是 $s$ 的后缀；$t$ 在 $s$ 中至少出现 $3$ 次。

如果 $ne_n$ 在中间出现过至少一次，那么答案就是 $ne_n$。
否则取 $ne_{ne_n}$，次长 border 至少出现 $4$ 次，满足限制条件。

submisson

NC16638

2024牛客暑期多校训练营3

妈的你不知道我不会证明也不会猜吗。

一定有一个 $8$ 不在边界，保留一个即可。

抽象下题意：$x = D$，每次使 $x \to \vert x - a_i \vert$ 。

令 $[a]$ 表示 $a_i$ 的一个线性组合。

如果不反弹，$x$ 显然形如 $D - [a]$，其中 $a_i$ 的系数非负。

考虑第一次反弹，$x$ 形如 $[a] - D$，其中 $a_i$ 的系数非负。

此时再减若干 $a_i$，$[a]$ 的系数可能出现负数，$x$ 的形式仅取决于 $[a], D$ 的大小。

那么 $\min \bigg\vert [a] - D \bigg\vert$，根据裴蜀定理拓展，$[a]$ 是所有 $\gcd$ 的倍数，容易得到答案。

预处理从 $i$ 开始跑一小轮的结果 $c_i$，和长度 $len_i$。

倍增求出 $p_{i, k}$ 表示从 $i$ 开始走 $2^k$ 小轮到什么位置，$s_{i, k}$ 表示 $2^k$ 小轮的结果和。

对于每一大轮，二分步数，求出能确定结果的最小步数。

牛魔贪心。

我们想消耗尽可能少的体力，最小化来回次数：$R$ 个人过去，$L$ 个人回来，每次过去 $R - L$ 个人。

总来回次数 $x = \lceil \dfrac{n - R}{R - L} \rceil$。

如果一个人有体力 $h_i$，那么他最多可以来回 $a_i = \lfloor \dfrac{h_i - 1}{2} \rfloor$。

一个显然的必要条件为 $\sum \min(a_i, x) \ge L \times x$。

证明他也是充分的：

每次让最大的 $L$ 个 $a_i$ 减 $1$，显然 $\sum \min (a_i', x) \ge L \times (x - 1)$，然后即可归纳证明。

（把最大的 $L$ 个中不在对岸的运到对岸，其他随便运）

如果存在一个数出现次数超过 $n + 1$，一定无解，因为 $(2, 3), (4, 5), \cdots, (2n- 2, 2n - 1)$ 要求不同。

对于所有 $x \ne y$ 的牌，存在很朴素的构造。

优先考虑 $x = y$ 的牌。

我们每次将 $val \ne lst$ 且剩余数量最大的牌放到右侧，如果有剩余则用 $x \ne y$ 的牌插空，最后补齐所有的 $x \ne y$。

~~题解称这样是一定有解的，我会证我来看你干什么。~~

对 $n$ 个串建出 trie 树。

题目要求的过程即在树上走 $n$ 次，每次走完把这个串删掉。

对于一个节点 $x$，记 $sz(x)$ 表示以 $x$ 为根有多少个叶子（有多少串以该点为前缀）。

那么在上述过程中从 $x$ 出发恰好往左走 $sz(l)$ 次，恰好往右走 $sz(r)$。

即 $f_{x, y}$ 表示序列中恰好存在 $x$ 个 $1$ $y$ 个 $0$ 的最大概率，每次抉择当前选 $0$ 还是选 $1：

\[f_{x, y} = \max\bigg( p \times f_{x - 1, y} + (1 - p) \times f_{x, y - 1},\ p \times f_{x, y - 1} + (1 - p) \times f_{x - 1, y} \bigg) \]

我们发现每个点独立对应一个 01 操作序列，答案即 $\prod\limits_{x} f_{sz(l), sz(r)}$

HDU2024多校2

7450

\[\begin{aligned} & f_{x} = (1 - \frac{p_x}{15}) \times f_x + \frac{p_x}{15} \times \max_{y \in \text{son(}x)} f_{y} + 1\\ \\ \implies & f_x= \max_{y \in \text{son(}x)} f_{y} + \frac{15}{p_x}\\ \end{aligned} \]

可以自己实现一个有理数类。

7451：语法题。

7454

手动模拟：$12345678 \to 1357 \to 15$，比较 $s_1, s_5$ 个数即可。

7445

最大鸡爪数显然是 $\lfloor \dfrac{n}{3}\rfloor$，难点在于构造最小字典序。

如果鸡爪数 $\le 2$，直接特判掉。

考虑鸡爪数 $\ge 3$ 的情况，最小化最大中心的编号：

第一个鸡爪需要四个点。
第二个鸡爪必须新建一个中心，此时连向 $1, 2, 3$ 是最优的。
以此类推。

我们要让编号小的节点度数大，贪心的取 $1, 2, \cdots, n/3$ 作为鸡爪中心。

$1$ 向 $n/3 + 1, n / 3 + 2, n / 3 + 3$ 连边，$2$ 向 $1, n/3 + 1, n / 3 + 2$ 连边，$3$ 向 $1, 2, n/3 + 1$ 连边。

如果边数不够，不断新增节点与 $1$ 连边即可。

7447

最多三步是给暴搜的，~~你要模拟十二种转的方式~~，发现只有 $8$ 个角有用，等效为一个二阶魔方，简化代码。

实际上步数没有上界也能做，注意到一个角的三个面相对位置在旋转过程中不会改变。

我们让一个角的三个面按逆时针排列，并将最小的一面作为第一个元素，这样就建立了角与字符串的一一映射。

然后枚举八个角，看在原先的集合里有没有出现。

7452

如果直径经过点 $x$，那么一定能经过 $x$ 拓展一次的所有点，同样可以经过由 $x$ 拓展的点再拓展的所有点。

那么把经过 $m$ 轮变换后 $x$ 生成的点数作为权值求带权直径。

一个度数为 $d$ 的点在一轮变换后会生成 $2$ 个二度点，$d - 2$ 个三度点。

也就是：

\[f^m(d) = 2 \times f^{m - 1}(2) + (d - 2) \times f^{m - 1} (3) \]

将 $d = 2$ 和 $3$ 分别代入：

\[f^m(2) = 2^m,\ f^m(3) = 2^{m + 1} - 1 \]

所以

\[f^m(d) = (d - 1) \times (2^m - 1) + 1 \]

对于 $m \le 20$，直接算，不会超过 long long。

否则对于二元组 $(d - 1, 1)$ 做加减，比较大小以 $d - 1$ 为第一关键字，因为所有的 $1$ 加起来也没一个 $2^m - 1$ 大。

7456

7446

Codeforces Round 960 (Div. 2)

如果 $mx$ 有奇数个，先手是必胜态。否则第一步选 $mx$ 必败。

考虑选次大值 $mx'$，如果 $mx'$ 有奇数个，先手必胜，否则第一个必败态的 $mx$ 一定是先手取到。

因此有结论，如果存在数 $x$ 的出现次数为奇，先手必胜。

第一想法是 $[y, x]$ 全赋为 $1$，但这样做有缺陷：-1, -1, -1, 1, 1 的最大前缀不是 $5$ 而是 $1$。

如果 ....-1, 1, -1 1, 1, 1 -1, 1, -1, ...

就可以将 $y$ 之前的前缀和要么等于 $[0, -1]$ 要么等于 $[0, 1]$，无论哪种在加上长度大于 $1$ 的 $[y, x]$ 段后都符合条件。

第一次操作后：数组元素单调不降。

如果所有相同数值段长度都不小于 $2$，那么一次操作后数组整体平移。

第一次操作后数组可能还存在单个的数，那么再做一次就能满足上述条件了。

贪不了一点心。

什么时候会用到操作 $1$？花费 $k$ 次填满 $k + 1$ 行。

$f_{i, 0/1, 0/1}$ 表示在第 $i$ 行 $12$ 或 $34$ 有没有凸出来的最优方案。

显然 $f_{i, 1, 1}$ 这个状态是永远不优的，因为可以同样花费两次把 $i$ 和 $i + 1$ 直接填满。

\[\begin{aligned} f_{i, 0, 0} &= \min \begin{cases} f_{i - 1, 0, 0} + [a_i \ne 0] \\ \\ f_{i - 1, 1, 0} & a_i \le 2 \end{cases} \\ \\ f_{i, 1, 0} &= \min \begin{cases} f_{i - 1, 0, 0} + 1 & a_i \le 2 \\ f_{i - 1, 0, 1} + 1 & a_i \le 4 \end{cases} \\ \\ f_{i, 0, 1} &= f_{i - 1, 1, 0} + 1 & a_i \le 4 \end{aligned} \]

AtCoder Beginner Contest 363

D：先找到答案的长度，然后从高到低确定每一位，时间复杂度 $O(n + \log^2 n)$。

E：优先队列里存当前边界的点，有点出队就向四周拓展。

F：设计函数 $f(n)$ 返回 $n$ 的一个合法字符串。

如果 $n$ 已经合法，直接输出。

否则枚举 $i \le \text{ rev} (i)$ 的因子， $f(n) = i + f( \dfrac{n}{i \times \text{ rev}(i)}) + \text{ rev}(i)$，不难发现 $i^2 \le n$。

所有调用的 $f$ 都是 $n$ 的因子，不妨直接预处理，时间复杂度 $O\bigg( d(n)\sqrt n\bigg)$。

G：线段树分治 + 模拟费用流，jly 写了 1h，待补。

HDU2024多校1

7440

7434

7433

7435

7438

7436

2024牛客暑期多校训练营2

对于奇数，简单的取 $x \oplus 1$ 即可，特判 $1$ 无解。

对于偶数 xxxx1000，把末尾的 $0$ 砍掉就行了，答案为 $x - \text{ lowbit } x$。

还需证明所有的 $x = 2^k$ 无解，如果 $x \oplus y = d$，显然 $d$ 是小于 $k$ 的 $2$ 的次幂，这样 $y = x \oplus d > x$ 矛盾。

首先证明，最优路径的横坐标可以单调不降。

枚举左端点，求出左端点一直到 $n$ 会走到拿个 $(tx, ty)$，看 $(tx, ty)$ 和 $(x, y)$ 差了多少。

找到离左端点最近的作用范围为 $(\Delta x, \Delta y)$ 的后缀，那么该后缀之后的所有点都能作为右端点。

根号分治。

如果 $k < \sqrt n$，直接 $k^2$ 跑 prim。

2024牛客暑期多校训练营1

暴力做法是维护一颗线段树，支持区间加区间推平，注意推平标记在 add 之前下传。

稍微分析一下就是求 $\sum i \times a_i$，从维护后缀转化到维护前缀，可以做到线性。

H：语法题。

把原序列划分成两部分：$S_0 = \{a_i \mid 1 \not\in a_i \},\ S_1 = \{a_i \mid 1 \in a_i \}$。

显然 $S_0$ 中元素不会出现出现在子序列中。

如果当前 $S_1$ 的一个子集满足按位与等于 $1$，那么同属 $S_1$ 的该子集的超集也能满足条件。

所以 $A$ 能满足条件当且仅当 $S_1$ 按位与等于 $1$。

枚举 $S_1$ 的大小：

\[\sum_{i = 1}^{n} \begin{pmatrix}n\\i\end{pmatrix} \times (2^{i} - 1)^{m - 1} \times 2^{(n - i)\times (m - 1)} \]

正难则反，用 A 题答案减去非法方案。

设当前有 $i$ 个奇数，称 $j$ 为特殊位当且仅当 $i$ 个数里只有一个第 $j$ 位为 $0$（$i > 1$）。

显然非法方案的充要条件是每个数至少对应一个特殊位。

定义 $f_{i, j}$ 表示 $i$ 个数，对应 $j$ 个特殊位的方案数：$f_{i, j} = i \times (f_{i - 1, j - 1} + f_{i, j - 1})\quad j \ge i,\ f_{i, i} = i!$。

这里相当与钦定了位数是单调递增的，在 $f_{i - 1, j - 1}$ 转移时需要考虑 $i$ 插在哪个位置。

那么方案数即：

\[\sum_{i = 2}^n \begin{pmatrix}n\\i\end{pmatrix} \times 2^{(n - i)\times (m - 1)} \sum_{j = i}^{m - 1} \begin{pmatrix}m - 1\\j\end{pmatrix} \times f_{i, j} \times (2^i - i - 1)^{m - j - 1} \]

I：大模拟，不会想写。

模数等于 $2^{21}$，于是只要求答案的前 $21$ 位。

注意到只对末尾操作，前缀不受影响，于是令 $s_i = s - p_{i - 1}$，$s$ 是当前总和。

按位计算，第 $d$ 位为 $1$ 当前仅当 $\sum\limits_{i = 0}^{n - 1} [s - p_i\text { 第 } d \text{ 位为一}]$ 是奇数。

稍作转化：$\sum\limits_{i = 0}^{n - 1} [s - p_i \bmod 2^{d + 1} \ge 0]$。

记 $s' = s \bmod 2^{d + 1},\ x = -p_{i - 1} \bmod 2^{d + 1}$，保证 $s',x \in [0, 2^{d + 1})$。

现在求满足 $(s' + x) \bmod 2^{d + 1} \ge 2^d$ 的 $x$ 的范围。

$s' \le 2^d$，$x \in [2^d - s', 2^{d + 1} - s')$。
$s' > 2^d$，$x \in [0, 2^{d + 1} - s') \cup [2^d + 2^{d + 1} - s',2^{d + 1})$。

树状数组维护区间和。

Codeforces Round 958 (Div. 2)

数据范围没必要推公式，发现多重集中的非一元素最多一个，时间复杂度 $O(n/k)$。

首先所有连续的 $0$ 都可以缩成一个，如果 $1$ 的数量大于 $0$ 的数量，直接取整个区间即可。

否则每次操作一定是 $101\to 1$ 的形式，即不断删一个 $01$，最后一定有剩余，直接判无解。

第二个数往后的最高位一定是 $1$，第三个数往后的次高位一定是 $1$，以此类推。

因此可以这样构造：第二个数最高为 $1$，次高位为 $0$，第三个数次高位为 $1$，下个位为 $0$。

这样是一定能构造的，且长度最长。

一上来想的跑最大权独立集是假的，因为删除后不能保证后续操作最优。

$f_{x, i}$ 表示 $x$ 在第 $i$ 轮被删除的最小代价，方程很好写，主要 $i$ 的上界怎么证明。

NOI2024-div2模拟赛66

NOI2024-div2模拟赛65

$a_i^2 + a_j = x^2 \implies a_j = (x - a_i)(x + a_i)$。

预处理 $a_i$ 的因子，时间复杂度 $O(m \ln m)$，我直接根号枚举也不慢。

std 的线段树 + 单调栈没看懂，更好写的 cdq 分治做法：

判断 $[l, r]$ 合法的条件很简单：$\max[l, r] - \min[l, r] = r - l$。

假设当前在处理 $[l, r]$，左端点 $i \in [l, mid]$，右端点 $j \in [mid + 1, r]$。

预处理 $mx_i/mx_j$ 表示从分治中心到 $i, j$ 的后缀/前缀最大，同样处理 $mi_i/mi_j$。

极值在同一侧，拿都在左边举例：

枚举 $i$，那么 $j = i + mx_i - mi_i$，判断是否满足限制条件即可。
极值不在同侧，假设 $mx_i > mx_j$ 且 $mi_i > mi_j$。

从大到小枚举 $i$，发现无论哪个条件的 $j$ 都是单调不降的，双指针维护合法区间，哈希表统计答案。

时间复杂度 $O(n\log n)$。

如果 $(a, b)$ 合法且 $a\to c$ 有长度为 $2$ 的路径，且 $(b, d) \in E$，则 $(c, d)$ 也合法。

反过来如果 $(a, b)$ 对于某个 $c$ 合法，则一定能从 $(c, c)$ 拓展过来。

考虑 bfs，设 $(a, b, 0)$ 表示 $(a, b)$ 合法，$(a, b, 1)$ 表示从合法状态往 $a$ 走了一条边，$(a, b, 2)$ 表示合法状态往 $a$ 走两条边。

$O(n^3)$ 暴力：$f_{l, r} = \begin{cases}\max(g_{l, r}, f_{l + 1, r - 1})\\ \min \bigg(\max(f_{l, mid}, f_{mid + 1, r})\bigg) \end{cases}$。

如果枚举答案 $lim$，转化为可行性问题：是否能仅用 $g_{i, j} \le lim$ 删掉整个序列。

二分答案，bitset 优化：

\[\begin{aligned} \implies &f_{i, j} = f_{i + 1, j - 1} \land[g_{i, j} \le lim]\\ \\ \implies & f_{i} = f_{i} \text{ bitwise or } f_{j + 1} & f_{i, j} = \text{ true} \end{aligned} \]

$O(\dfrac{n^3}{w}\log n)$，很幽默的复杂度，但是能过。

std 做法：

每次把 $lim$ 增大 $1$，相当于加入一对新的 $(i, j)$，尝试更新 $f_{i, j}$。

进一步的，如果 $f_{i, j} = \text{ true}$，根据转移方程，尝试更新 $f_{i - 1, j + 1},\ f_{i, *},\ f_{*, j}$。

把所有合法状态放入队列，$O(n ^2)$ 个状态，每个状态利用 _Find_next $O(\dfrac{n}{w})$ 更新，时间复杂度 $O(\dfrac{n^3}{w})$。

整体二分

莫队

CF1000F *2400

$O(n\sqrt n \log n)$ 的做法非常脑残，但是过不去。

值域分块维护，这样可以 $O(\sqrt n)$ 查询，$O(1)$ 修改。

CDQ 分治

P3810 【模板】三维偏序（陌上花开） *省选/NOI-

先按 $a_i$ 排序，设当前分治区间为 $[l, mid, r]$：

递归 $[l, mid]$ 同时让左边按 $b_i$ 排序。
递归 $[mid + 1, r]$ 同时让右边按 $b_i$ 排序。

归并左右两边，树状数组处理二维偏序。

也可以排好序后对第二维继续 cdq，这种方法能过拓展到更高纬度的偏序问题。

CF1093E *2400/省选/NOI-

考虑映射 $f(a_i) = i$，令 $b_i \to f(b_i)$，这样可以把一组询问 $[l_a, r_b],[l_b, r_b]$转化为：

\[\sum_{i = l_b}^{r_b} \big[b_i \in [l_a, r_a]\big] \]

把 $b$ 写成点对 $(i, b_i)$，每个点权值为 $1$，上式即 $x \in [l_b, r_b], y\in [l_a, r_a]$ 的点 $(x, y)$ 的权值和。

根据二位前缀和的经验，一个询问拆成四个询问，每次求出 $\{(0, 0) ,\ (x, y)\}$ 的矩阵和。询问点显然权值为 $0$。

我们对每个点多维护一个时间戳，表示加入平面的时间戳。

比如时间 $t$ 时交换 $x, y$，相当于在 $(x, b_x)$ 加入一个权值为 $-1$ 的点，同时在 $(x, b_y)$ 加入一个权值为 $1$ 的点。

这样就转化为：对于每个点 $(x, y, t)$，求出所有 $x_i \le x, y_i \le y, t_i \le t$ 的点权和，三维偏序模板。

AT_joisc2014_i *省选/NOI-

先按横坐标排序，设当前分治区间为 $[l, r]$，保证两侧的纵坐标严格递减。

在 $[l, mid]$ 自上而下枚举左下角，考虑哪些右上角不可能成为答案。

如果 $a, b$ 满足 $a_y < b_y$ 且 $a_x < b_x$，那么 $b$ 就没用了，因此对右边维护一个单调栈，满足横坐标递增。

再考虑左边其他点的影响：

纵坐标小于当前点的没有影响。
横坐标小于当前的的没有影响。

所以左边维护一个横坐标递减的单调栈，每次根据栈顶元素的纵坐标在右边单调栈二分。

P5094 [USACO04OPEN] MooFest G 加强版 *普及+/提高

把原问题分成两份： $x_i \le x_j \land v_i \le v_j$；$x_i \ge x_j \land v_i < v_j$。

二维偏序树状数组就行，不过可以写 cdq 练练手。

P4690 [Ynoi2016] 镜中的昆虫 *NOI/NOI+/CTSC

如果只有单点修是好做的，把 $(i, pre_{i})$ 看成点，就是 CF1073E 的带修矩阵和。

现在证明：$m$ 次区间修改后 $pre_i$ 的变动次数是 $O(n + m)$ 的。

类似 odt 的维护方式，我们把序列划分为若干连续颜色段。

考虑把 $[l, r]$ 从 $v$ 改变为 $v'$，$pre$ 值发生改变的点只有：$l$，离 $r$ 最近的 $v$ 点，离 $r$ 最近的 $v'$ 点。

把修改看成一个删除后新建的过程，删除一个 $(l, r, v)$ 最多需要改变 $1$ 个点，新建一个 $(l, r, v')$ 最多需要改变 $2$ 个点。

最坏情况下，一个节点贡献三次修改。

而一次推平操作最多新建 $3$ 个节点（左右 split 出来两个，最后推平一个），所以 $pre_i$ 的修改次数是 $O(n + m)$ 的。

对整个序列和每种颜色都开一个 odt，暴力修改 $pre_i$ 即可。

线段树分治

LOJ121「离线可过」动态图连通性

对于一条存活时间在 $[l, r]$ 的边 $e$，把他加到所有被 $[l, r]$ 覆盖的节点，有点像标记永久化。

并查集维护连通性，由于在遍历线段树时需要回溯，所有该并查集需要支持回退。

路径压缩会破坏树的形态，采用启发式合并，把有改动的地方压入栈中，回退即逆操作。

一共会加 $O(n \log n)$ 条边，外层线段树也是 $O(n \log n)$，加边操作 $O(\log n)$，总复杂度 $O(n\log^2 n)$。

P5787 二分图 /【模板】线段树分治 *提高+/省选−

分治部分与上题一致，主要怎么用并查集判二分图。

设 $x_{1/0}$ 分别为 $x$ 的偶点/奇点，$(x, y) \in E \iff (x_0, y_1) \land (x_1, y_0)$。

这样保证了奇偶相同的点只能通过偶数条边到达。

如果在连接 $(x, y)$ 时 $x_0, y_0$ 同属一个集合，那么加上这条边后就会出现奇环。

GYM105231F

思路很好想，合并很毒瘤。

CF603E *3000/NOI/NOI+/CTSC

结论：存在边集使得每个点度数为奇 $\iff$ 图中不存在奇连通块。

证明：

充分性：每条边对总度数贡献为 $2$，总度数是偶，矛盾。

必要性：对于一个偶联通块，随便找一棵生成树，自下而上跑以下算法：

如果儿子向自己连了偶数条边，选连向父亲的边；否则不选。

这样可以保证除根之外都满足条件，又因为总度数为偶，除根外总度数为奇，所以根的度数也为奇。

先考虑静态问题：

按边权排序，不断往里加边，奇连通块数是非增的，如果不存在奇连通块就得到了答案。

考虑动态的过程，按时间往里加边，如果当前符合条件，尝试删掉最大的边。

我们发现一条边在在答案边集的时间是一段连续区间，称为这条边的存活时间。

按边权排序，边权小的边存活时间右端点就越大。

因此我们从右往左分治，从小到大更新存活时间，这也说明在分治过程中 kruscal（近似）的指针是非降的。

设当前访问叶子对应时间 $t$，当前扫到的边出现时间为 $i$，那么他的存活时间为 $[i, t]$。

不断加边，直到奇连通块数为 $0$，说明只用前 $x$ 条边就能在时间 $t$ 符合条件，第 $x + 1$ 条边无论怎样都不会出现在 $\ge t$ 的答案中。

边分治边求出存活时间，内套可撤销并查集，时复 $O(m\log m\log n)$。

CF576E *3300/NOI/NOI+/CTSC

NOI2024-div2模拟赛64

“如果 N 市存在一条单向道路 $(u,v)$，那么保证从街区 $v$ 出发无法到达街区 $u$。”

容易发现（我没发现），把只通过无向边连接的连通块缩点，剩下的是一张 DAG。

每个连通块内跑 dij，按拓扑序更新。

B：圆方树 dp，待补。

拆位，设 $a_i = \sum b_{i, k} \times 2^{k}$，则：

\[(a_i \oplus a_j)^2 = \sum\limits_{k_1}\sum\limits_{k_2} [b_{i, k_1} \ne b_{j, k_1}][b_{i, k_2} \ne b_{j, k_2}] 2^{k_1 + k_2} \]

记 $f_{k_1, k_2, 0/1, 0/1}$ 表示以 $x$ 为根的子树与 $x$ 距离不大于 $k$ 的集合中第 $k_i$ 为 $v_i$ 的元素数量。

容易做到 $O(log ^2 V)$ 的插入/删除，并同时维护答案，赛时没想到拆位，只做到了 $O(V^2)$。

启发式合并是很好写的，总复杂度 $O(n\log n \log^2V)$，能够通过。也可以树上差分少掉一个 log。

KD Tree

FHQ Treap

CF1725K *2500/省选/NOI-

操作一：题解的按排名分裂好像有 bug，更简单的做法：

如果 $x$ 是根，$root = \text{merge}(ls, rs)$，并将 $root$ 的父亲改为空。
否则设 $x$ 的父亲为 $p$，设 $y = \text{merge}(ls, rs)$，把 $y$ 挂到 $x$ 原来的位置，父亲改为 $p$。
插入修改后的 $x$。

操作二：把 $x$ 到根的所有懒标记下传，直接输出 $x$ 的值。

操作三：$[l, mid]$ 打上 $l - 1$，$[mid + 1, r]$ 打上 $r + 1$，对树的形态并不会有影响。

CF809D *2900/省选/NOI-

设 $f_j$ 表示长度为 $j$ 的演的上升序列结尾最小值。

\[f_j = \begin{cases} \min(f_j, l) & f_{j - 1} < l\\ f_{j - 1} + 1 & f_{j - 1} \in [l, r)\\ f_j & f_{j - 1} \ge r \end{cases} \]

$f$ 数组严格上升，平衡树优化 dp。

在小于 $l$ 的最大的位置后面插入 $l$，后面的位置相当整体右移。
把 $[l, r)$ 区间加一并右移一位，而第一步已经右移好了。
对于 $\ge r$ 的部分保持不变，而数组已经偏移，所以把 $\ge r$ 的最小的删掉。

最后答案就是平衡树的大小（神题，数形结合）。

CF702F *2800/省选/NOI-

把物品按题意排序，设当前物品需要花费 $v$。

现在要把剩余钱数 $\ge v$ 的人钱数减 $v$，操作数加 $1$。

如果剩余数组是有序，很容易用平衡树维护，把 $\ge v$ 的部分分裂出来并打上标记。

但是钱数减 $v$ 后数组不能保证数组的有序性。

发现剩余钱数 $\ge 2v$ 的部分是能保证的，唯一有问题的是 $[v, 2v)$ 这一段。

不妨 split 成三段：$[0, v)[v, 2v)[2v, +\infty)$。

暴力修改第二段，每次 $v$ 至少减少一半，所以暴力插入次数不超过 $O(n\log V)$。

时间复杂度 $O(n\log n\log V)$。

李超线段树

~~LCT~~

支持的操作：1. 加入一条线段；2. 询问与 $x = k$ 交点纵坐标最大的线段编号。

维护的信息（标记）：完全覆盖当前区间且在区间中点数值最大的编号。

插入：设 $[l, r]$ 原来标记为 $i$，现加入 $j$。

如果 $[l, r]$ 没有标记，直接打上 $i$ 返回。否则 $i, j$ 没法合并，需要递归地下传。

如果 $f_{i}(mid) < f_j(mid)$，交换 $i, j$。

（已经默认了 $i$ 在 $mid$ 比 $j$ 优）如果 $f_{j}(l) > f_{i}(l)$，说明在左边 $j$ 会反超 $i$，把 $j$ 传给左儿子。

如果 $f_{j}(r) > f_{i}(r)$，说明在右边 $j$ 会反超 $i$，把 $j$ 传给右儿子。

有 $O(\log n)$ 个节点需要下传，每次下传只会走 $O(\log n)$ 个点（一次只走一边），总复杂度 $O(\log^2 n)$。

查询：类似标记永久化，把根到叶子的路径取 $\max$。

P4655 [CEOI2017] Building Bridges *省选/NOI−

朴素转移：$f_i = f_j + (h_i - h_j)^2 + s_{i - 1} - s_j$。

出现当前信息与转移信息的乘积，化成斜优（单调队列/平衡树维护凸包）的形式：

\[f_j + h_j^ 2 - s_j = 2h_i\times h_j + (f_i - s_{i - 1} - h_i^2) \]

这很不对，考虑怎么转换能够用李超树维护。

把 $y, b$ 交换一下：

\[s_{i - 1} + h_i^2 - f_i = 2h_j\times h_i + (s_j - f_j - h_j^ 2) \]

这样就是每次加一条直线，询问 $h_i$ 处的最大 $y$。

CF932F *2700/省选/NOI−

$f_i = b_j \times a_i + f_j$，现在只要合并子节点李超树。

一种方法是启发式合并，只要把有改动的节点丢进栈里，就可以做到与修改同阶的清空，时复 $O(n\log^2n)$。

直接合并李超树也是可行的。具体来说：如果合并的 $x, y$ 都不为空，先递归得到左右儿子，再把 $y$ 的标记传给 $x$。

时间复杂度不是很显然：

除合并外，其他地方复杂度不超过 $O(n\log n)$。
由于加的是直线，李超树中的标记（直线）数量不超过 $n$。
在合并过程中，如果两棵树都不为空，要么将另一条直线直接废弃，要么使这条直线的深度加一。
线段树树高只有 $O(\log)$，所以复杂度等于树高乘直线数等于 $O(n\log n)$。

P4069 [SDOI2016] 游戏 *NOI/NOI+/CTSC

CF1303G *2700/省选/NOI−

NOI2024-div2模拟赛63

?一共三道题你出两道交互。。

题目暗示很明显了，最后要询问两组十次得到答案。

显然用第一组得到数的组成，再由第二组得到组成的排列。

复杂分块

P4117 [Ynoi2018] 五彩斑斓的世界 *NOI/NOI+/CTSC

第二分块（？突刺贯穿的第二分块）。

区间所有大于 $x$ 的减 $x$ $\iff$ 区间小于等于 $x$ 的加 $x$（维护懒标记）

设当前区间最大值为 $v$。

$2x \ge v$，把 $[x + 1, v]$ 并到 $[1, v - x]$ 上，花费 $O(v - x) \times O(\text{ds})$ 使 $v$ 减小 $O(v - x)$。
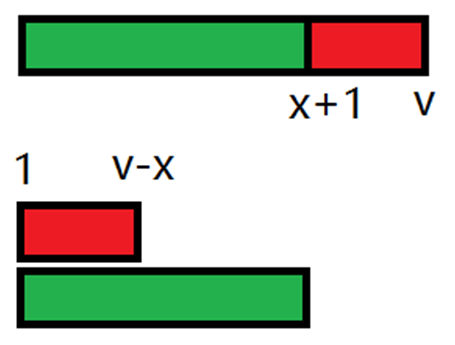
$2x < v$，把 $[1, x]$ 并到 $[x + 1, 2x]$ 上，花费 $O(x) \times O(\text{ds})$ 使 $v$ 减小 $O(x)$。

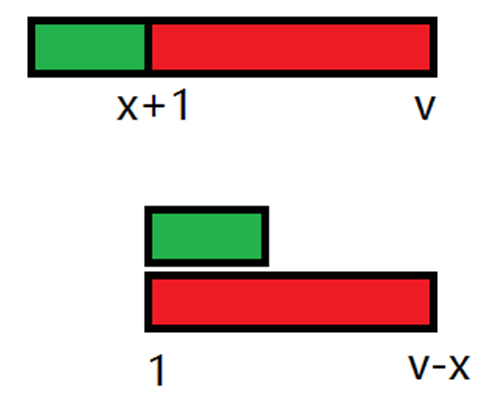
对于每个块，初始 $v$ 是 $O(n)$ 的，根据上述操作，把 $v$ 减到 $0$ 只要 $O(n) \times O(\text{ds})$。

整块修改：并查集维护每个值的数量（每次把一个根接到另一个根下面），每个块 $O(n)$。

散块修改：把每个位置的当前值还原，暴力重构，暴力修改，单次 $O(\sqrt n)$，每个询问对应 $O(1)$ 个散块。

整块查询：单次 $O(1)$。散块查询：暴力，单次 $O(\sqrt n)$。总时间复杂度 $O(n \sqrt n)$。

离线每个块对答案的贡献，这样空间复杂度也是 $O(n)$ 的。（inline 和 register 记岔了，inline 在高版本还是有用的）

CF1375H *3300/NOI/NOI+/CTSC

树套树

可持久化数据结构

P2839 [国家集训队] middle *省选/NOI−

如果 $x$ 是长度为 $n$ 的序列的中位数，那么 $\sum [y \ge x] \ge \lceil\frac{n}{2}\rceil$。

钦定 $x$，把小于 $x$ 的值赋为 $-1$，大于等于 $x$ 的值赋为 $1$，得到 $a'$。

如果 $\sum_{i = l}^r a_i' \ge 0$，说明 $[l, r]$ 的中位数大于等于 $x$，答案有单调性，考虑二分。

对于每个不同的 $x$，如何得到对应的 $a'$。这件事很容易用主席树做到。

现在要最大化 $l \in [x_1, y_1],\ r \in [x_2, y_2]$ 的子段和。

只要维护 $[x_1, y_1]$ 的最大后缀，$[x_2, y_2]$ 的最大前缀已经 $(y_1, x_2)$ 的整段和即可。

不在当前区间的 $x$ 是否可能成为答案？设所选区间 $a$ 个小于 $x$，$b$ 个大于等于 $x$，选第 $a + 1$ 个数不会比 $x$ 劣。

动态 DP

值域变换法

如果转移方程形如 $dp_i = F(dp_{i - 1}, info_i)$ 且值域 $M$ 很小。

可以把这个方程当成一种值域上的变换（$dp_{i - 1} \to dp_{i}$）。

在线段树上操作，对于区间 $[l, r]$，进来 $dp_{l - 1}$，出去 $dp_r$。

我们不关心 $dp_{l - 1}$ 具体是什么，只需要计算所有 $x \in $M 经过 $\text{F}_{l, r}$ 的 $dp_r$

左右儿子合并就是变换的复合，显然满足结合律。

值域变换支持单点修改，区间查询。

CF1076G *3000/NOI/NOI+/CTSC

感觉这比后面的紫简单很多。。？

如果 $(i, i + m]$ 中存在必败点，直接跳过去，先手必胜。

否则两个人的最优决策都是把 $a_i$ 耗完，如果 $a_i$ 是奇数，先手必胜，否则必败。

先朴素 dp，$f_i$ 表示第 $i$ 个点是不是先手必胜。

\[f_i = \begin{cases} 0 & \bigg(\sum\limits_{j = i + 1}^{i + m} f_i = m\bigg) \land\bigg(a_i \equiv 1\pmod 2\bigg) \\ 1 & \text{otherwise} \end{cases} \]

值域是什么呢？我们可以把后面 $m$ 个数压成一维，则值域就是 $2^m$，最大才 $32$。

乍一看已经做完了，但值域变换不支持区间修改。

如果 $d$ 是偶数，忽略这一操作。

否则类似翻转操作，我们可以一开始就对 $[l, r]$ 记录两个变换：翻转后的和原来的，然后用懒标记维护是否翻转即可。

实际上只要关心右边第一个必败点的位置，值域缩小为 $m$。

广义矩乘

定义广义矩乘 $(\oplus, \otimes)$：$C_{i, j} = \bigoplus\limits_{k = 1}^n A_{i, k} \oplus B_{k, j}$。

其中：$\oplus$ 满足交换律，$\otimes$ 满足结合律和交换律，且 $\oplus$ 对 $\otimes$ 有分配律。

比较常见的：$(\max, +)$，$(\min, +)$。

我们也可以写出该运算下的单位矩阵，对 $(\max, i)$ 来说：$I = \begin{bmatrix}0 & -\infty &\cdots & - \infty\\ -\infty & 0 & \cdots & -\infty \\ \vdots & \vdots & \ddots & \vdots \\ -\infty & -\infty & \cdots & 0\end{bmatrix}$。

如果用 dp 值和有关信息组成的向量 $F$ 满足 $F_i = M \times F_{i - 1}$，那么 dp 可以写成广义矩乘。

一些本来只能迭代计算的修改能够支持合并操作，从而支持单点修改，区间询问。

一定要注意是左乘还是右乘（鉴定为被矩阵快速幂惯的）。

SP1716 *提高+/省选−

朴素方程：$f_i = a_i + \max(f_{i - 1}, 0)$ 表示以 $i$ 结尾的最大子段和。

写成 $(\max, +)$ 矩乘：

\[\begin{bmatrix} f_i\\ 0\\ mx_i\\ \end{bmatrix} = \begin{bmatrix} a_i & a_i & -\infty\\ -\infty & 0 & -\infty\\ a_i & a_i & 0 \end{bmatrix} \begin{bmatrix} f_{i - 1}\\ 0\\ mx_{i - 1}\\ \end{bmatrix} \]

对于一个询问，初始向量为 $\begin{bmatrix}0\\0\\-\infty\end{bmatrix}$。

CF1609E *2400/提高+/省选−

$f_{i, 0/1/2}$ 表示 $s$ 的前 $i$ 位已经和 "abc" 匹配了 0/1/2 位的最小代价。

令 $abc \to 012$。

\[\begin{aligned} f_{i, j} &= f_{i - 1, j} + [s_i = j]\\ \\ f_{i, j} &= f_{i - 1, j - 1} + [s_i \ne j - 1]\\ \end{aligned} \]

写个 $3\times 3$ 的矩阵随便维护一下。

CF750E *2600/省选/NOI-

写法和上题基本一致，先对字符集做映射：$2017 \to 0123,\ 6 \to 4$。

\[\begin{aligned} f_{i,j} &= f_{i - 1, j} + [s_i = j \lor (j = 3 \land s_i = 4)]\\ \\ f_{i, j} &= f_{i - 1, j - 1} + [s_i \ne j - 1] (+ \infty) \end{aligned} \]

CF1681E *2600/省选/NOI−

dp 状态 $f_{i_{0/1}, j_{0/1}}$ 表示 $i$ 的第 0/1 扇门走到 $j$ 的第 0/1 扇门的最短路。

暴力转移是 $O(qn^2)$ 的。

但是每次的转移矩阵是相同的，线段树维护区间乘法。

\[\begin{bmatrix} f(i_0, j_0)\\ f(i_0, j_1)\\ f(i_1, j_0)\\ f(i_1, j_1)\\ \end{bmatrix} = \begin{bmatrix} d(j - 1_0, j_0) & d(j - 1_1, j_0) & \infty & \infty\\ d(j - 1_0, j_1) & d(j - 1_1, j_1) & \infty & \infty\\ \infty & \infty & d(j - 1_0, j_0) & d(j - 1_1, j_0)\\ \infty & \infty & d(j - 1_0, j_1) & d(j - 1_1, j_1)\\ \end{bmatrix} \begin{bmatrix} f(i_0, j-1_0)\\ f(i_0, j-1_1)\\ f(i_1, j-1_0)\\ f(i_1, j-1_1)\\ \end{bmatrix} \]

树剖套 DDP

如果 dp 方程能写成：$F_x = M_{x \text{ 与轻儿子}} \times F_{\text{重儿子}}$。

那么可以将 $O(n)$ 的修改优化到 $O(\log n^2)$。（全局平衡二叉树能优化到单 log）

具体来讲，对于每个节点维护一个矩阵 $M_x$ 记录 $x$ 和其亲儿子的贡献。

不难发现，最后的 $F_x$ 即从 $x$ 到当前重链底端所有 $M$ 之积乘上空节点（叶子的儿子）的向量。

考虑单点修改 $x$：与 $x$ 在同一重链的祖先不会发生变化。

需要修改的节点有：$x,\ fa_{top_x},\ fa_{top_{fa_{top_x}}} \cdots$，只有 $O(\log n)$ 个。

P4719 【模板】"动态 DP" *省选/NOI−

$f_{x, 0/1}$ 为在 $x$ 的子树中选/不选 $x$ 的最大权独立集。

$g_{x, 0/1}$ 为在 $x$ 的子树中不考虑重儿子选/不选 $x$ 的最大权独立集。

\[\begin{aligned} \begin{bmatrix} f_{x, 0} & f_{x, 1} \end{bmatrix} = \begin{bmatrix} f_{son_i, 0} & f_{son_i, 1} \end{bmatrix} \oplus \begin{bmatrix} g_{i,0} & g_{i, 1}\\ g_{i, 0} & -\infty\\ \end{bmatrix} \\ \\ \bigg(C = A \oplus B \implies C_{i, j} = \max (A_{i,k} + B_{k, j})\bigg) \end{aligned} \]

P6845 [CEOI2019] Dynamic Diameter *省选/NOI−

$f_{x, 0}$ 表示从 $x$ 往下走的最长链长度加上到父亲的权值。$f_{x, 1}$ 表示 $x$ 子树中的最长链长度。

设轻儿子集合为 $l(x)$。

\[\begin{bmatrix} f_{x, 0}\\ f_{x, 1}\\ 0 \end{bmatrix} = \begin{bmatrix} w_{x} & -\infty & w + \max\limits_{y \in l(x)}(f_{y, 0})\\ \max\limits_{y \in l(x)}(f_{y, 0}) & 0 & \max\bigg(\max\limits_{y \in l(x)} f_{y, 1},\ \max\limits_{y, z \in l(x)}( f_{y, 0} + f_{z, 0})\bigg)\\ -\infty & -\infty & 0 \end{bmatrix} \begin{bmatrix} f_{son, 0}\\ f_{son, 1}\\ 0 \end{bmatrix} \]

用堆（multiset）动态维护轻儿子信息，时间复杂度 $O(n\log^3n)$。

DP 套 DP

特指一类 dp，把一个需要 dp 判定的判定性问题改成计数性问题。让你计算在某一条件下判定为真的输入有多少个。

判定性 dp 本身值域很小，且 f[i] 只与很近的几个 f[j] 有关。

可以将 f[j]...f[i] 这一段状压成 S。

计数性 dp[i][S] 表示输入 i 个数，判定性 dp 最近几个状态为 S 的输入数量。

说人话，把内层 dp 的结果作为外层 dp 的状态进行转移。

本质是一个 NFA 转 DFA 的过程。

AT_abc228_g *2649/省选/NOI−

建个图（NFA）理解一下。

行为右部点，列为左部点，$i, j$ 连有一条权值为 $g_{i, j}$ 的无向边。

要求长为 $2n$，边权相连后不同的路经数。

如果状态仅为 $f_{i, j}$ 表示第 $i$ 步走到 $j$ 的方案数是不对的，会重复计算。

更改状态为 $f_{i, S}$ 表示能使第 $i$ 步走到集合 $S$ 中的所有点的序列数，不同集合中的序列一定不同。

枚举第 $k \to k + 1$ 步的边权 $x$：

\[f_{k, S} \to f_{k + 1, T = \{j \ \mid \exists i \in T,\ g_{i, j} = x \}} \]

在外层循环枚举这一步的决策，在内层循环枚举上一步的状态 $S$，并由 $S \to T$，由于上一步里不同集合答案不同，保证了这一步是不重不漏的。

LOJ6274. 数字

朴素做法：枚举 $V$。

设 $f(pos, l_1, r_!, l_2, r_2)$ 表示在第 $pos$ 位，限制条件的满足情况为 $l_1, r_1, l_2, r_2$ 时是否存在 $x \lor y = T$ 且 $x\land y = V$。

这是一个存在性问题，可以数位 dp 解决。

存在性改计数性，把后面四个状态压成一个 $i \in [0, 16)$，再把所有 $f_{pos, i}$ 的值压进计数 dp 的状态。

新的 $f_{pos, i}$ 表示第 $i$ 为，满足状态集合为 $i$ 的有多少 $V$。

BZOJ3864. Hero meet devil

P4590 [TJOI2018] 游园会 *省选/NOI−

P5279 [ZJOI2019] 麻将 *NOI/NOI+/CTSC

NOI2024-div2模拟赛62

如果一个环只有一个点度数大于 $2$，显然单独把这个环分出来是最好的。

如果一个环不只一个点度数大于 $2$，与其单独取环，不如把环分给出去的链。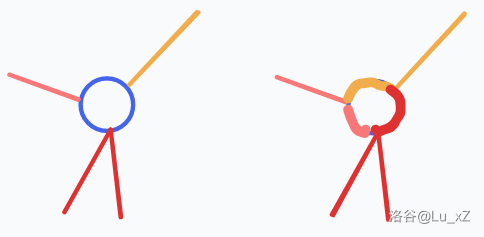

考虑最少要多少条链才能覆盖整张图。稍作转化：链 = 链的端点数 / 2。

如果 $i$ 的度数 $d_i$ 是偶数，那么可以两两匹配出边和入边，$i$ 可以不是端点。

否则 $i$ 一定是端点，答案为 $\sum [d_i \bmod 2 = 1]$ 加上单独的环个数。

NOI2024-div2模拟赛61

A：整体二分或SA，待补。

注意 $V = N /d \le 100$，考虑容斥。

设 $f_{i, j, x, y}$ 表示前 $i$ 个位置，找到了 $j$ 个位置，钦定了 $x + y$ 个位置大于 $a_i$，选了其中 $x$ 个的容斥系数。

记 $z = \frac{a_i + 1}{d}$，转移时考虑选/不选，容斥/不容斥。

\[\begin{aligned} f_{i, j, x, y} = &+ f_{i - 1, j, x, y} \times (1 - p_i)\\ &+ f_{i - 1, j - 1, x, y} \times p_i\\ &- f_{i - 1, j, x, y - z} \times (1 - p_i)\\ &- f_{i - 1, j - 1, x - z, y} \times p_i \end{aligned} \]

那么答案等于 $\sum f_{m, j, x, y} \times \text{满足 }x,y \text{ 限制且找到的 } j \text{ 个位置不小于 } n \text{ 的方案数}$。

记 $z = N - (x + y) \times d, \ w = n - xd$，表示还剩多少钥匙，$j$ 个位置还差多少。

如果 $z < w$，方案数为 $0$。

如果 $w < 0$，说明已经满足 $j, x, y$ 的限制已经满足，剩下随便放：$\begin{pmatrix}z + m - 1\\m - 1\end{pmatrix}$。

否则问题等价于前 $j$ 个位置不小于 $n$ 的方案数。

从前往后放钥匙，满足第 $i$ 个钥匙的位置不小于 $i - 1$ 个钥匙。

枚举第 $w$ 个钥匙的位置，方案即：

\[\sum_{i = 1}^{j} \begin{pmatrix}w - 1 + i - 1\\i - 1\end{pmatrix}\begin{pmatrix}z - w + m - i\\m - i\end{pmatrix} \]

时间复杂度 $O(m^2V^2)$。

对纵坐标分治，设当前分治中心为 $mid$。

$a_y \le mid$ 的权值最大的点和 $b_y > mid$ 的权值最大的点两者至少取其一（显然）。

这样有贡献的点对只有 $O(n\log n)$ 个。使其中一维有序，正反各做一边扫描线。

7/3

被爆了，老老实实加训。

NOI2024-div2训练赛60

A：写了一个以 vector 为键的神秘背包，复杂度和正解应该是一样的。

对于 $P \le 3000$，直接以 $f(pos, sum, mod)$ 为状态数位 dp，时间复杂度 $O(10^2\times \log^2N \times P)$。
对于 $P > 3000$，枚举数位和 $s$，时间复杂度 $O(90 \times \dfrac{N}{P})$，南外神机跑的飞快。

$(i, j)$ 为 $1$ 当且仅当第 $i$ 行和第 $j$ 列的总操作次数。

如果有 $i$ 行操作了奇数次，$j$ 列操作了奇数次，那么当前矩阵有 $i\times (m - j) + (n - i)\times j$ 个 $1$。

枚举 $i, j$，检查 $1$ 的个数是否为 $s$。

只考虑行，先 $n$ 个里面选 $i$ 个，剩下 $R - i$ 次操作必须两个两个分配给每行，即 $ x_1 + x_2 + \cdots + x_n = \frac{R - i }2$ 的非负整数解。

一对合法的 $(i, j)$ 贡献为：

\[\begin{pmatrix}n\\i\end{pmatrix} \begin{pmatrix}m\\j\end{pmatrix}\begin{pmatrix}\frac{R - i}2 + n - 1\\n - 1\end{pmatrix}\begin{pmatrix}\frac{C - j}2 + m - 1\\m - 1\end{pmatrix} \]

不难求出最多操作次数 $tot$。

有了 $tot$ 限制后，由于本题只求方案数，不需要再考虑花费。

假设当前在第 $i$ 步，只关心三元组 $(x, y, z)$ 表示有 $x$ 个位置已经和 $b$ 相同，$y$ 个位置再走一步相同，$z$ 个位置再走两步才相同。

用一个向量 $F_i$ 表示第 $i$ 步时所有状态的方案数。

\[\begin{bmatrix} f_{0, 0, n}\\ f_{0, 1, n - 1}\\ f_{0, 2, n - 2}\\ \vdots\\ f_{n, 0, 0}\\ s_{n, 0, 0}\\ \end{bmatrix} \]

由于题目要求不超过 $tot$ 的 $f_{n, 0, 0}$，所以再记录 $s_{n, 0, 0}$ 表示合法方案的前缀和。

系数矩阵很好推（$(x, y, z) \to x\times (x - 1, y, z + 1)$），时间复杂度 $O(n^6\log V)$。（还有 $O(n^2)$ 的大跌做法）

$k \in \{0, 1, 2\}$，依次分讨。

不妨先做弱化版：计算满足 $k$ 的限制的无向图个数，不一定联通。

$k = 0$：

\[calc_0(n, m) = \begin{pmatrix}\frac{n(n - 1)}{2}\\m\end{pmatrix} \]

$k = 1$：

\[calc_1(n, m) = calc_0(n - 1, m - 2)\begin{pmatrix}n - 1\\2\end{pmatrix} \]

$k = 2$：

\[calc_2(n, m) = \begin{cases} calc_0(n - 2, m - 3)\times (n - 2)^2 & 1,2 \text{ 之间有边} & n \ge3\\ \\ calc_0(n - 2, m - 4)\times \begin{pmatrix}n - 2\\2\end{pmatrix}^2 & 1,2 \text{ 之间没边} & n \ge 4\\ \end{cases} \]

回归原问题，用 $calc_k(n, m)$ 减去不连通的情况。

这里可以枚举 $1$ 所在连通块大小及边数，剩下的部分任意连边。

\[\begin{aligned} f_{0,i, j} = calc_0(i, j) &- \sum_{k}\begin{pmatrix}i - 1\\k - 1\end{pmatrix}\sum_{l} f_{0, k, l} \times calc_0(i - k, j - l)\\ \\ f_{1,i, j} = calc_1(i, j) &- \sum_{k}\begin{pmatrix}i - 1\\k - 1\end{pmatrix}\sum_{l} f_{1, k, l} \times calc_0(i - k, j - l)\\ \\ f_{2,i, j} = calc_2(i, j) &- \sum_{k}\begin{pmatrix}i - 2\\k - 2\end{pmatrix}\sum_{l} f_{2, k, l} \times calc_0(i - k, j - l) &\text{包含 }2\\ \\ &- \sum_{k}\begin{pmatrix}i - 2\\k - 1\end{pmatrix}\sum_{l} f_{1, k, l} \times calc_1(i - k, j - l) & \text{不含 }2\\ \\ & (j \ge i - 1) \end{aligned} \]

区间 DP

AT_abc217_f *提高+/省选-

$g_{i, j}$ 表示 $i, j$ 是否相连，设 $f_{i, j}$ 为把 $[i, j]$ 消去的方案数。

如果 $g_{i, j} = 1$：$f_{i, j} \gets f_{i + 1, j - 1}$。

对于一般情况，不难想到枚举中转点：

\[f_{i, j} \gets \sum f_{i, k} \times f_{k + 1, j} \times \begin{pmatrix}\frac{j - i + 1}{2}\\ \frac{k - i + 1}{2}\end{pmatrix} \]

可以默认左右各自的消去顺序已经确定，只要考虑如何分配即可。

但是这样是不对的，对于 ()()()... 的情况会重复计算，因此强制让 $i, k$ 匹配即可。

\[f_{i, j} \gets \sum g_{i, k} \times f_{i + 1, k - 1} \times f_{k + 1, j} \times \begin{pmatrix}\frac{j - i + 1}{2}\\ \frac{k - i + 1}{2}\end{pmatrix} \]

P3607 [USACO17JAN] Subsequence Reversal P *省选/NOI-

$f_{i, j, L, R}$ 表示 $[i, j]$ 段，值域为 $[L, R]$ 的最大长度。

小值域到大值域：$f_{i, j, L, R} \gets \max \bigg(f_{i, j, L + 1, R}, f_{i, j, L, R - 1}\bigg)$。
小区间到大区间：$f_{i, j, L, R} \gets \max \begin{cases}f_{i + 1 , j, L, R} + [a_i = L] \\ f_{i, j - 1, L, R} + [a_r = R]\end{cases}$。

考虑所谓翻转操作：

1 6 2 3 4 3 5 3 4
  ^         ^ ^ ^
  |         +-+ |
  +-------------+

翻转序列两侧可以两两匹配，正好符合区间 dp 的步骤。

尝试翻转左右两端元素：$f_{i, j, L, R} \gets f_{i + 1, j - 1, L, R} + [a_i = R] + [a_j = L]$。

CF1922F *2500

状态很好想，之前是因为转移成环所以没补，结果发现也可以没环。

$f_{l, r, x}$ 表示把 $[l, r]$ 推平成 $x$ 的最小代价。

$g_{l, r, x}$ 表示 $[l, r]$ 中不含 $x$ 的最小代价。

\[g_{l, r, x} = \min \begin{cases} g_{l, mid, x} + g_{mid + 1, r, x}\\ \\ g_{l, r, y} + 1\quad y \ne x \end{cases} \quad f_{l, r, x} = \min \begin{cases} f_{l, mid, x} + f_{mid + 1, r, x}\\ \\ g_{l, r, x} + 1 \end{cases} \]

树形 DP

AT_abc223_g *提高+/省选−

直接用最大匹配转移比较复杂，树是二分图：最大匹配 = 点数 - 最大独立集。

也就是求满足下列条件的点数：

\[n - \text{ 原图最大独立集} = (n - 1) - \text{挖掉 }x\text{ 后的新图的最大独立集} \]

剩下的问题即与 CF1984E 相同。

第一遍扫描求出 $f_{x, 0/1}$ 表示在以 $x$ 为根的子树中选/不选 $x$ 的最大独立集：$\begin{cases}f_{x, 0} = \sum \max(f_{y, 0}, f_{y, 1})\\f_{x, 1} = \sum f_{y, 0}\end{cases}$。

第二遍扫描求出 $g_{x, 0/1}$ 表示选/不选 $x$ 的最大独立集：$\begin{cases}g_{x, 0} = \max\bigg(g_{fa, 1}, f_{x, 0} + g_{fa, 0} - \max(f_{x, 0}, f_{x, 1})\bigg) \\ g_{x, 1} = f_{x, 1} + g_{fa, 0} - \max(f_{x, 0}, f_{x, 1}) \end{cases}$。

状压 DP

AT_abc328_g *提高+/省选−

从 $1 \sim n$ 依次枚举 $a_i$ 的位置。

设当前 $b$ 已经被填的集合为 $S$，记 $f_{S}$ 表示集合为 $S$ 时的最小花费。

考虑 $f_{S}$ 怎么去更新后续节点。

设 $l = \vert S\vert + 1$，则 $1 \sim l - 1$ 已经填完了，接下来要填的一定是 $l\sim r$ 的连续一段。

枚举 $r$，从 $b$ 的 $p$ 位置开始填（$[p, p + len)$ 都不能被填过）：

\[f_{S \cup [l, r]} \gets f_S + c + \sum_{i \in {[l, r]}} \vert a_i - b_{p + i- l} \vert \]

摸底考。打得一坨还有 rk9，结果全是初中生。。upd：全是小学生，换组了。

F：离散化，建权值线段树。每个节点记录：

$cnt$：当前区间有多少个数。
$s_i$：当前区间内的坐标模 $5$ 相同的数之和。

上传子树信息：

\[\begin{cases} cnt = l_{cnt} + r_{cnt}\\ \\ s_i = l_{s_i} + r_{s_j} & j + l_{cnt} \equiv i \pmod 5 \end{cases} \]

G：暴力 + 二分，喜提全场唯一 40 pts。

从下至上扫描，枚举哪一种颜色不选，此时所选区间的矩阵已经确定。

还要考虑没有上边界的点，枚举每一对颜色相同的相邻点作为左右边界。

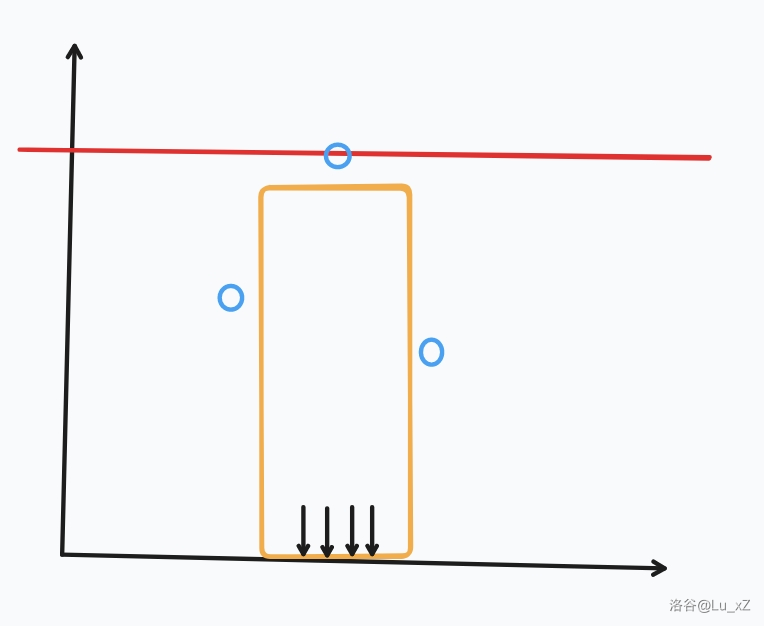
H：初中✌泰牛。

把字符串补成等长，少的部分用 # 补齐，默认 # 的字典序小于 a。

对字符集做一个映射：$\# \to 0,\quad a\sim z\to 1 \sim 26,\quad ? \to 27$。

预处理 $g_{x, y, z, a, b}$ 表示 $s_{1} = x,\ s_{2} = y,\ s_3 = z$ 且 $x, y$ 的大小关系位 $a$，$y, z$ 大小关系为 $b$ 是的方案数。

其中大小关系 $\text {cmp}(x, y) = \begin{cases} 0 & x < 1\\ 1 & x = y \\2&x > y \end{cases}$。

设 $g_{i, 0/1, 0/1}$ 表示前 $i$ 位 $s_1$ 和 $s_2$ 的字典序大小为 $0/1$（$0$ 为相等，$1$ 为 $s_1 < s_2$）， $s_2$ 和 $s_3$ 的字典序大小为 $0/1$ 时的方案。

设 $s_{1, i} = A,\ s_{2, i} = B,\ s_{3, i} = C$，枚举大其小关系 $x, y$。

\[f_{i, j, k} \gets g_{A, B, C, x, y} \times f_{i - 1, a, b} \]

$a$ 为 $0$ 则 $x$ 不为 $2$，同理 $b$ 为 $0$ 则 $y$ 不为 $2$。
若 $a$ 为 $1$ 或 $x$ 为 $0$，则 $j$ 为 $1$，同理若 $b$ 为 $1$ 或 $y$ 为 $0$，则 $k$ 为 $1$。

posted @ 2024-07-03 01:02 Lu_xZ 阅读(28) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部