学习笔记:Miller-Rabin 与 Pollard-Rho
Miller_Rabin
首先考虑方程 \(x^2 \equiv 1 \pmod n\)。
可以写成 \((x + 1)(x - 1) = kn\)。
当 \(n\) 为素数时,只可能 \(n \mid x + 1\) 或 \(n \mid x - 1\),反之合数不满足。
得到结论:
在模素数意义下,一个数的平方等于 \(1\) 当且仅当这个数同余于 \(1\) 或 \(-1\)。
我们知道,对于素数 \(p\),有 \(x^{p - 1} \equiv 1 \pmod p\)。
那 \(x^{\frac{p - 1}{2}}\) 呢?
将 \(p - 1\) 看做 \(2^k\cdot u\) 的形式,其中 \(u\) 是奇数。
依次计算 \(x^u, x^{2u}, \cdots, x^{p - 1}\),每个数都是前一个数的平方。
- 如果最后一项不为 \(1\),则 \(p\) 一定不是质数。
- 如果中间一项为 \(1\),而它的前一项不是 \(-1\),则 \(p\) 一定不是质数。
只要选取合适的底数进行检验,那么排除合数的概率很大。
取前 \(12\) 个质数作为底数,那么 \(64\) 位整数范围内都能保证正确性。
bool miller_rabin(ll n) {
if(n <= 2 || !(n & 1)) {
return n == 2;
}
static int base[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
ll u = n - 1, k = 0;
while(u % 2 == 0) u >>= 1, ++ k;
for(int x : base) {
if(x % n == 0) continue;
ll v = qpow(x, u, n);
if(v == 1 || v == n - 1) continue;
for(int i = 1; i <= k; ++ i) {
ll lst = v;
v = (__int128)v * v % n;
if(v == 1) {
if(lst != n - 1) return false;
break;
}
}
if(v != 1) return false;
}
return true;
}
Pollard_Rho
随机生成均匀分布在 \([0, n)\) 的整数,那么生成一个之前出现过的数的期望次数是 \(O(\sqrt n)\) 的。
定义伪随机生成器 \(f(x) = (x^2 + c)\bmod n\),\(c\) 是一个常数。
指定一个 \(x_0\),生成序列 \(x_0, f(x_0), f(f(x_0)), \cdots\)。
我们让前一项向后一项连边,得到下图:
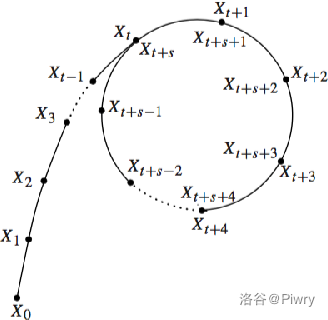
形如字母 \(\rho\),也是该算法名字由来。
对于 \(x_i = x_j\),显然有 \(n \mid x_i - x_j\)。
考虑 \(n\) 的一个因子 \(d\),一定存在 \(i, j\) 使得 \(d \mid x_i - x_j\)。
如何理解呢?
把序列 \(a\) 整体模 \(d\),那么在新图中会出现一个新环,环上相同的两点 \(x_i, x_j\) 即满足条件。
也就是说,找因子的过程等价于找环的过程。
如何找环?
初始令 \(x = y = x_0\),每次让 \(x = f(x), y = f(f(x))\),\(y\) 的速度比 \(x\) 快,找到环后一定会追上 \(x\)。
令 \(d = \gcd(x - y, n)\),\(x, y\) 为模 \(d\) 意义上的环上同一点。
如果 \(d > 1\),返回 \(d\),否则继续找环。
找到模 \(n\) 意义下的环是 \(O(n^{1/2})\) 的,找到模 \(d\) 意义下的环是 \(O(n^{1/4})\) 的。
pollard_rho 的朴素实现,理论复杂度 \(O(n^{1/4}\log n)\)。
mt19937_64 mt(time(nullptr));
ll pollard_rho(ll n) {
uniform_int_distribution<ll> u0(0, n - 1);
ll c = u0(mt);
auto f = [&](ll x) {return ((__int128)x * x + c) % n;};
ll x = u0(mt), y = x;
while(1) {
x = f(x), y = f(f(y));
ll d = __gcd(abs(x - y), n);
if(d != 1) {
return d;
}
}
}
gcd 调用过于频繁,衍生出倍增优化版本。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll qpow(__int128 a, ll b, ll p) {
ll ret = 1;
while(b) {
if(b & 1) ret = ret * a % p;
b >>= 1;
a = a * a % p;
}
return ret;
}
bool miller_rabin(ll n) {
if(n <= 2 || !(n & 1)) {
return n == 2;
}
static int base[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
ll u = n - 1, k = 0;
while(u % 2 == 0) u >>= 1, ++ k;
for(int x : base) {
if(x % n == 0) continue;
ll v = qpow(x, u, n);
if(v == 1 || v == n - 1) continue;
for(int i = 1; i <= k; ++ i) {
ll lst = v;
v = (__int128)v * v % n;
if(v == 1) {
if(lst != n - 1) return false;
break;
}
}
if(v != 1) return false;
}
return true;
}
mt19937_64 mt(time(nullptr));
ll pollard_rho(ll n) {
uniform_int_distribution<ll> u0(0, n - 1);
ll c = u0(mt);
auto f = [&](ll x) {return ((__int128)x * x + c) % n;};
ll x = 0, y = 0, s = 1;
for(int k = 1;; k <<= 1, y = x, s = 1) {
for(int i = 1; i <= k; ++ i) {
x = f(x);
s = (__int128)s * abs(x - y) % n;
if(i % 127 == 0) {
ll d = gcd(s, n);
if(d > 1) return d;
}
}
ll d = gcd(s, n);
if(d > 1) return d;
}
}
ll mx;
void get_factor(ll n) {
if(miller_rabin(n)) {
mx = max(mx, n);
return;
}
if(n == 4) {
mx = max(mx, 2ll);
return;
}
ll p = pollard_rho(n);
while(p == n) p = pollard_rho(n);
get_factor(p);
get_factor(n / p);
}
void solve() {
ll x; cin >> x, mx = 0;
get_factor(x);
if(mx == x) {
cout << "Prime\n";
return;
}
cout << mx << '\n';
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int T;
cin >> T;
while(T --) {
solve();
}
return 0;
}


