训练记录（Jun.）

6/24

CF1883F *1400

性质题。

如果子串的开头不是这个元素的第一个位置 x...xaaaaaa，子序列不唯一。

如果子串的结尾不是这个元素最后一个位置 aaaaaax...x，子序列不唯一。

如果子串的开头是一个位置，结尾是最后一个位置 ...xaaaaaay...，子序列唯一。

CF1759E *1500

嗑药顺序确定后，贪心策略也确定，直接枚举嗑药顺序。

CF1862E *1600

手推一下式子，前后项相消，$s = a_{i_1} + a_{i_2} + \cdots a_{i_k} - i_k \times d$。

枚举最后一个数，维护少于 $m$ 个数的最大子序列和。

CF1196D2 *1600

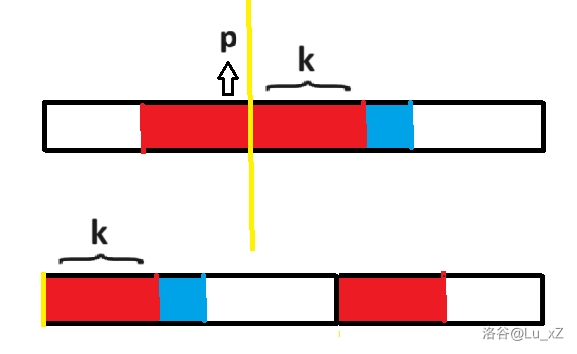
整串只会变成 RGB... GBR... BRG... 三种，记录代价的前缀和，依次检查每个长度为 $k$ 的区间。

CF1085D *1700

猜了发结论，过了：所有权值均分给叶子，答案即 $2s / \sum [d_i = 0]$。

有一个叶子不放，答案变大。
放一个在其他地方，答案可能变大。

CF833A *1700

$a$ 乘 $k$，$b$ 乘 $k^2$，又或 $a$ 乘 $k ^2$，$b$ 乘 $k$。

最后 $a \times b$ 一定是某个数 $k$ 的三次方且 $k \mid a\land k \mid b$。（显然也是充分条件）

CF336C *1800

枚举结果的最高位 $i$。

把所有包含 $i$ 这一位的数与起来，把他的最低位和答案比较。

（有没有可能撤销某些元素使得最低位变大？不可能，因为所有数都包含这个最低位）

CF863C *1800

根据鸽巢原理，$9$ 轮后必有循环，所以暴力枚举循环节。

另有 $O(\log k)$ 的倍增做法：$f_{i, j, k}$ 和 $g_{i, j, k}$ 分别表示从 $i, j$ 开始， $2^k$ 轮后两名选手的状态和得分。

CF535C *1900

显然可以二分右端点，只需考虑如何 check。

设一轮最多 $m$ 个，可以走 $t$ 轮。

证明：当且仅当 $\max(h_1, h_2, …, h_n) \le t$ 且 $\sum h_i < t \times m$ 时，$h$ 是 $(m, t)$ 可消去的。

必要性显然，证明充分性。

使用归纳法，一次操作后 $h'$ 是 $(m, t - 1)$ 可消去的，则 $h$ 是 $(m, t)$ 可消去的。

序列至少有 $m$ 个非零元素：
- 等于 $t$ 的元素至多 $m$ 个，否则条件不满足。
- 把最大的 $m$ 个元素每个减一。最大元素最多等于 $t - 1$，和最多 $m(t - 1)$，符合 $(m, t - 1)$ 可消去的条件。
序列非零元素个数小于 $m$：
- $h'$ 的最大元素至多等于 $t - 1$，和至多 $m(t - 1)$，符合 $(m, t - 1)$ 可消去的条件。

CF1032D *1900

要么经过直线，要么不经过，一共就 $5$ 种方案，直接枚举。

CF366D *2000

枚举答案的右端点，此时左端点有单调性，二分答案。合并符合条件的边，并查集判断 $1$ 和 $n$ 是否联通。

P2756 飞行员配对方案问题

源点向左部连容量为 $1$ 的边。
左部向右部连容量为 $1$ 的边。
右部向汇点连容量为 $1$ 的边。

P3254 圆桌问题

源点向左部连容量为 $r_i$ 的边。
左部向右部连容量为 $1$ 的边。
右部向汇点连容量为 $c_i$ 的边。

2188. 无源汇上下界可行流

给定一个包含 $n$ 个点 $m$ 条边的有向图，每条边都有一个流量下界和流量上界。

求一种可行方案使得在所有点满足流量平衡条件的前提下，所有边满足流量限制。

已知流网络 $G$ 和其可行流 $f$，转化为只有上界的 $(G',\ f')$。

\[\begin{aligned} & c_{lower}(u, v) \le f(u, v) \le c_{upper}(u, v)\\ \\ \implies & 0 \le f(u, v) - c_{lower}(u, v) \le c_{upper}(u, v) - c_{lower}(u, v)\\ \end{aligned} \]

把新图中每条边的容量设为 $c_{upper}(u, v) - c_{lower}(u, v)$ 即可满足容量限制。

此时 $\sum \bigg( f(v, u) - c_{lower}(v, u) \bigg) ?= \sum \bigg( f(u, v) - c_{lower}(u, v) \bigg) $，不一定满足流量守恒。

设 $in_u = \sum c_{lower}(v, u),\ out_u = \sum c_{lower}(u, v)$。

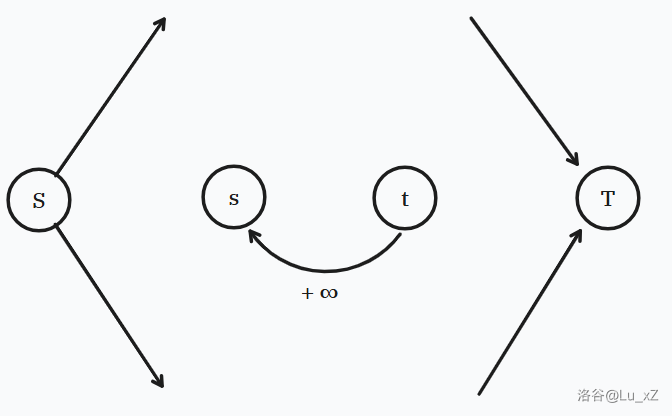
虚拟一个源点 $S$，汇点 $T$。

$in_u > out_u$，$S$ 向 $u$ 补满 $in_u - out_u$。
$in_u < out_u$，$u$ 向 $T$ 流掉 $out_u - in_u$。

也就是 $G$ 的任意可行流 $f$，与 $G'$ 的一条最大流 $f'$ 一一对应。从 $S$ 连出的边必须满流，否则原图可行流不存在。

2189. 有源汇上下界最大流

给定一个包含 $m$ 个点 $m$ 条边的有向图，每条边都有一个流量下界和流量上界。

给定源点 $s$ 和汇点 $t$，求源点到汇点的最大流。

先考虑有源汇上下界可行流怎么做。

在汇点 $t$ 与源点 $s$ 间连一条容量为 $+ \infty$ 的边 $e$，$s$ 和 $t$ 就流量守恒了，转化为无源汇上下界可行流。

设原图为 $G$，新图为 $G'$，新图中任意一条满流为 $f_0'$，对应原图中的 $f_0$。

此时 $s \to t$ 的流量 $\vert f_{0:s \to t}'\vert$ 等于 $e$ 此时的流量。

设 $f'_{s\to t}$ 为残量网络 $G'_{f_0'}$ 中 $s \to t$ 的一条可行流。

现证明：原图可行流与 $f'_{s \to t}$ 一一对应。

任意 $f'_{s \to t}$ 能对应一个原图可行流 $f_1$。
- $S,\ T$ 皆已满流必，定不被 $f'_{s\to t}$ 经过，所有操作只在中间部分完成。
- 把 $f'_{s\to t}$ 与 $f'$ 相加（复合），多出来的部分可以从 $e$ 退回，得到一条新的满流 $f''$。
- $f''$ 变换为 $f_1$。
任意 $f_1$ 能对应一个 $f'_{s \to t}$。
- $f_1$ 变换为 $f''$。
- 把 $f''$ 与 $f_0'$ 相减，有关 $S,T$ 的边全部抵消，容量为 $0$。
- $f'' - f_0' = f_{s \to t}'$。（$s,\ t$ 换成不是 $S,\ T$ 的其他两点也成立）。

因此，任取一个 $f_0'$，在 $G_{f_0'}$ 上跑 $s \to t$ 的增广路，最后还原即得原图最大流。

设 $f_{0:s\to t}'$ 为 $f_0'$ 中 $s \to t$ 的一段。

\[\vert f'_{0:s\to t} + f'_{s\to t} \vert = \vert f'_{0:s\to t}\vert +\vert f'_{s\to t} \vert \]

若求原图最大流：最大化 $\vert f'_{s \to t} \vert$，在 $G_{f_{0}'}'$ 上跑 $s \to t$ 的最大流（删掉 $e$）。

若求原图最小流：最小化 $\vert f'_{s \to t} \vert$，在 $G_{f_{0}'}'$ 上跑 $t \to s$ 的最大流。

6/21

P3698 [CQOI2017] 小Q的棋盘 *提高+/省选−

法一：贪心。

到达一个点的花费只有两种：去了不回来：$1$ 次；去了回来：$2$ 次；

最大化去了不会来的点的个数，显然取从根开始的一条最长链。其余节点可以从链上延伸并花费两次到达。

法二：树背包。

设 $f_{x, i, 0/1}$ 表示从 $x$ 开始走到 $x$ 的子树，还剩 $i$ 步，不回/回到 $x$ 的最大点数。

⟲：$f_{x, i, 1} = f_{x, i - j - 2, 1} + f_{y, j, 0}$。
↙⟲：$f_{x, i, 0} = f_{x, i - j - 2, 0} + f_{y, j, 1}$。
⟲↘：$f_{x, i, 0} = f_{x, i - j - 1, 1} + f_{y, j, 0}$。

P1823 [COI2007] Patrik 音乐会的等待 *普及+/提高

维护一个非递增的单调栈。

对于 $i$，找到大于 $h_i$ 的第一个位置，贡献即该位置到栈顶的区间长。

P2946 [USACO09MAR] Cow Frisbee Team S *普及/提高−

能力值很大，但 $F$ 很小，且最后求的是 $F$ 的倍数的方案，不难想到在模 $F$ 意义下跑 01 背包。

P3558 [POI2013] BAJ-Bytecomputer *普及+/提高

首先，$i + 1$ 的操作不回影响 $i$ 及其之前，告诉我们转移方向一定是从前往后的。

设 $f_{i, -1/0/1}$ 表示第 $i$ 位为 $-1/0/1$ 的最小代价，按题意转移即可。

P1156 垃圾陷阱 *普及+/提高

$f[hight] = \max(life)$。

$f_{i, j}$ 表示前 $i$ 个垃圾，高度为 $j$ 时的最大生命值。$f_{i, j} = \begin{cases}f_{i - 1, j} + F_j & j \ge T_i \\ f_{i - 1, j - H_{i}} & j - H_i \ge T_i\end{cases}$。

P4158 [SCOI2009] 粉刷匠 *提高+/省选

行里做一遍背包，列里做一遍背包，然后就蓝了（

CF1151D *1600

变量只有 $j$，最小化 $\sum (a_i - b_i) j$。

排序不等式：如果$x < y,\ a < b$，因为 $(y - x)(b - a) > 0$，所以 $yb + xa > ya + xb$。

CF242D *2100

构造一种方案：如果当前 $a_i = b_i$，操作 $i$，此时 $b_i = a_i + 1$ 且在往后操作中不可能再等于 $a_i$。更新相邻节点。

每个点最多非法一次，不存在无解情况。

CF5E *2400

在最高峰两侧的点不可能相互看到（同为最高峰除外），于是把最高峰放到第一个位置，破环成链。

后续操作与 P1823 一致，单调栈的应用。

按上述操作跑一遍后还是会有问题：2 2 1 1，后两个 $1$ 和第一个 $2$ 没被记入答案。

这种例外只会发生在第一个元素和其他之间，所以放到最后特判。

CF1400G *2600

如果 $m = 0$：枚举集合大小 $i$，设包含 $i$ 的元素个数为 $cnt_i$，那么方案为 $\begin{pmatrix}cnt_i\\i\end{pmatrix}$，差分维护。

考虑一般情况。容斥 $m$ 个条件，如果选了 $x$ 个条件，那么与这些条件有关联的 $j$ 个元素必须都选。

设 $l = \max l_k, r =\min r_k,\ k \in {J} $，那么对于大小 $i \in [l, r]$ 的集合要加/减 $\begin{pmatrix}cnt_i - j\\i - j\end{pmatrix}$ 的贡献。

6/20

P2518 [HAOI2010] 计数 *提高+/省选-

如果数位小于 $n$：直接多重集排列 + 插板。

如果数位等于 $n$：试填法。

*P5005 中国象棋 - 摆上马 提高+/省选-

典型的状压 dp，需要考虑别马脚的情况。滚动数组优化。

P2606 [ZJOI2010] 排列计数 *提高+省选-

发现元素的偏序关系形成一棵以 $p_1$ 为根的完全二叉树。

那么 $f_i = \begin{pmatrix}sz_i - 1\\sz_L\end{pmatrix} f_L \times f_R$。

本题存在 $n > p$，也就是说 $p \mid n!$，不能直接快速幂求逆。

lucas 定理：$\begin{pmatrix}n\\m\end{pmatrix}\bmod p = \begin{pmatrix}\lfloor\frac{n}{p}\rfloor\\ \lfloor\frac{m}{p}\rfloor\end{pmatrix} \times \begin{pmatrix}n \bmod p\\ m\bmod p\end{pmatrix} \bmod p$。

$n \bmod p < p$，所以后面一项可以阶乘预处理 $[0, p - 1]$ 的范围，前面则继续递归。

P4544 [USACO10NOV] Buying Feed G *提高+省选-

1.$O(N^2K^2)$

设 $f_{i, k}$ 表示当前在第 $i$ 家商店，饲料数恰好为 $k$ 的最小代价。

考虑几个因素：

第 $i$ 家商店前已经买了 $k$ 吨。
第 $i$ 家商店买了 $p$ 吨。
上一家买的商店为 $j$。

于是得到最朴素的方程：

\[f_{i, p + k} = \min\bigg(f_{j, k} + k^2(X_i - X_j) + C_i \times p\bigg) \]

2.$O(N^2K + NK^2)$

我们发现在上述转移方程中，只有最后一项含有 $p$。

不妨设 $g_{i, k} = \min\bigg(f_{j, k}+ k^2(X_i - X_j) \bigg)$，则 $f_{i, p + k} = \min(g_{i, k}) + C_i \times p$。

其中 $g_{i, k}$ 可以 $O(NK)$ 预处理，$f_{i, p + k}$ 可以 $O(K^2)$ 转移。

3.$O(N^2K)$

把关于 $i$ 的式子从 $g_{i, k}$ 中去除，重新定义 $g_{i, k} = \min\bigg(f_{j, k}- k^2\times X_j) \bigg)$

这样的好处在于 $g_{i, k} = \min(g_{i - 1, k}, f_{i - 1, k} - k^2 \times X_{i - 1})$ 是可以 $O(K)$ 递推的。

// 90 pts
for(int i = 1; i <= N; ++ i) {
    for(int p = 0; p <= a[i].f; ++ p) {
        for(int k = 0; k + p <= K; ++ k) 
            f[i][p + k] = min(f[i][p + k], g[k] + sq(k) * a[i].x +  ll(p) * a[i].c);
    }
    for(int k = 0; k <= K; ++ k) {
        g[k] = min(g[k], f[i][k] - sq(k) * a[i].x);
    }
}

4.$O(NK\log K)$

观察上述代码，复杂度瓶颈在于第一个循环。

不要枚举 $k, p$，直接枚举 $j = k + p$，那么会变成这样：

for(int j = 0; j <= K; ++ j) {
    for(int k = j; j - k <= a[i].f; -- k)		// k \in [j - a[i].f ,j] 
        f[i][j] = min(f[i][j], (g[k] + sq(k) * a[i].x - (ll)k * a[i].c) + (ll)j * a[i].c);
}

也就是

\[f_{i, j} = j \times C_i + \min\bigg( g_k + k^2 \times X_i - k \times C_i \bigg) \quad k \in [j - F_i, j] \]

后面的式子只关于 $i, k$，且是连续的一段，线段树维护区间最值。

正常做法：

设 $f_{i, j}$ 表示前 $i - 1$ 家店买了 $j$ 吨，走到 $i$ 的最小代价。

\[\begin{aligned} f_{i, j} &= f_{i - 1, k} + \bigg(X_i - X_{i - 1}\bigg)^2 \times j + C_{i - 1} \times (j - k)\\ \\ &= \bigg(f_{i - 1, k} -k \times C_{i - 1}\bigg) + C_{i - 1} \times j + d_{i - 1}^2 \times j & j - k \le F_{i - 1}\\ \end{aligned} \]

那么在遍历 $j$ 的同时，单调队列维护 $j - F_{i - 1}\sim j$ 的第一项最小值，时间复杂度 $O(NK)$。

P3522 [POI2011] TEM-Temperature *普及+/提高-

如果 $[L, R - 1]$ 可行，让每个点贪心的取他的前缀左端点最大，使得 $R$ 更容易满足。

如果 $R$ 小于 $[L, R - 1]$ 的左端点最大，说明 $[L, R]$ 不能非降，左端点右移。

|
|  |
|||| |  
||||||||
  L   R

单调队列维护区间最大。我们要求的东西是 $L\sim R$ 以及 $L$ 左边小于 $L$ 的部分。

P4360 [CEOI2004] 锯木厂选址 *省选/NOI-

CF131F *2000

法一：枚举左上角以及矩阵的宽，二分右边界。

法二：枚举矩阵上下界，双指针确定左右边界。

CF678D *1700

法一：多写几组，发现是等比数列。讨论公比为 $1$ 的情况。

法二：$\begin{pmatrix}g^n(x)\\1\end{pmatrix} = \begin{pmatrix}A&B\\0&1\end{pmatrix}\begin{pmatrix}g^{n - 1}(x)\\1\end{pmatrix}$，矩阵快速幂加速递推。

CF515E *2300

破环成链，每次询问都是一段连续区间。

将距离前缀和，要求 $\max\bigg(2h_x + 2h_y + (s_x - s_y)\bigg)$。

分开维护 $\max(2h + s)$ 和 $\max(2h - s)$。

如果两个最值的位置相同，再次询问不包含这个位置的最值。

P3047 [USACO12FEB] Nearby Cows G *普及+/提高

第一遍扫描求出以 $x$ 为根的子树中距离为 $i$ 的权值和：$\begin{cases} f_{x, 0} = w_x\\ f_{x, i} = \sum f_{y, i - 1} \end{cases}$。

第一遍扫描求出与 $x$ 距离为 $i$ 的权值和：$\begin{cases} g_{1, i} = f_{1, i}\\ g_{x, i} = f_{x, i} + g_{fa, i - 1} - f_{x, i - 2}\end{cases}$。

6/19

CF438D *2300

区间取模。还真就维护个区间 $\max$，如果模数大于 $\max$ 就不要往下递归了。

复杂度证明：

对于一个 $p \le x$，如果 $x \bmod p = r$，则 $x = kp + r$。

因为 $k > 0, r < p$，所以 $r < \dfrac{x}{2}$。

也就是对于一个数 $x$，只会取模 $O(\log x)$ 次。

外层再套一个线段树，时间复杂度 $O(n \log n\log V)$。

CF1051D *1700

朴素 dp，设 $f_{i, j, s}$ 表示前 $i$ 列，$j$ 个联通块，第 $i$ 列状态为 $s$ 的方案数，从 $f_{i - 1, j', t}$ 转移。

CF446C *2400

方法一：

证明结论：$f_{n + m} = f_{n + 1}f_{m} + f_{n, m - 1}$。

\[\begin{aligned} &\because\begin{pmatrix}1&1\\1&0\end{pmatrix}^n = \begin{pmatrix}f_{n + 1}&f_n\\f_n&f_{n - 1}\end{pmatrix}\\ \\ \texttt{又} &\because \begin{pmatrix}1&1\\1&0\end{pmatrix}^n\begin{pmatrix}1&1\\1&0\end{pmatrix}^m = \begin{pmatrix}1&1\\1&0\end{pmatrix}^{n + m}\\ \\ &\therefore f_{n + m} = f_n f_{m + 1} + f_{n - 1}f_m = f_{n + 1}f_m + f_{n}f_{m - 1} \end{aligned} \]

那么我们对于一个位置 $i$ 加上 $f_{i - L + 1}$ 等价于加 $f_{i}f_{-L} + f_{i + 1}f_{-L + 1}$。

那么对于线段树的一个节点 $(l, r)$，维护两个标记：

$\text{tag1} = \sum f_{-L}$。
$\text{tag2} = \sum {f_{-L + 1}}$。

那么这段区间最终会加 $\text{tag1}(f_l + \cdots f_{r}) + \text{tag2}(f_{l + 1} + \cdots f_{r + 1})$。

方法二：

先推个通项公式，顺便复习下生成函数。

\[\begin{aligned} F(x) &= f_1 x + f_2 x^2 + (f_1 + f_2) x^3 + \cdots \\ \\ &= x + x^2 + x^2 F(x) + x \bigg(F(x) - x\bigg)\\ \\ &= x^2F(x) + xF(x) + x \end{aligned} \]

所以：

\[\begin{aligned} F(x) &= \dfrac{x}{1 - x - x^2}\\ \\ &= x\bigg(\dfrac{c}{1 - ax} + \dfrac{d}{1 - bx} \bigg)\\ \\ &= \sum_{i \ge 1} \bigg(a^{i - 1}c + b^{i - 1}d\bigg)x^i \end{aligned} \]

待定系数解得：

\[\begin{cases} a = \dfrac{1 + \sqrt 5}{2}\\ \\ b = \dfrac{1 - \sqrt 5}{2}\\ \\ c = \dfrac{1}{\sqrt 5} \times \dfrac{\sqrt 5 + 1}{2}\\ \\ d = \dfrac{1}{\sqrt 5} \times \dfrac{\sqrt 5 - 1}{2} \end{cases} \]

所以

\[f_{n} = \dfrac{1}{\sqrt 5} \bigg[ (\dfrac{1 + \sqrt 5}{2})^n - (\dfrac{1 - \sqrt 5}{2})^n\bigg] \]

$\sqrt 5 \equiv 383008016 \pmod {1e9 + 9}$，不需要二次剩余，写个暴力也只要跑 1s。

一个修改 $(l, r)$ 即相当于在原序列上加两个等比数列。

具体来说，一段长为 $n$ 的区间 $[l, r]$ 只会加两种公比，$q_1 = \dfrac{1 + \sqrt 5}{2}, q_2 = \dfrac{1 - \sqrt 5}{2}$。

每次要加的东西都是 $\dfrac{1 - q^n}{1 - q}$ 乘上当前首项，所以对于两个公比分别维护一个标记即可。

CF558E *2300

题如其名：a simple task。

统计这段区间中每种字符的数量，按要求依次推平。（odt效率远高于线段树）

CF1114F *2400

$\varphi(n) = n(\dfrac{p_1 - 1}{p_1})(\dfrac{p_2 - 1}{p_2})\cdots(\dfrac{p_k - 1}{p_k})$

由于 $300$ 内的质数只有 $62$，所以只要在维护乘积的同时维护所含质因子的状态即可求出欧拉函数。

CF317B *2000

P4925 [1007] Scarlet的字符串不可能这么可爱 *普及+/提高

首先分析回文串的性质。

从一个回文串的中心看起，一定形如 ...xyx... 或 ...xx...。

换而言之，一个字符串不包含回文子串当且仅当任意连续三个位置互不相同。

很容易得到 50 pts 的 dp：$f_{i, x, y} = \sum f_{i - 1, y, z},\ x\ne y\ne z$。

再考虑没有位置限制的特殊情况：$1,2$ 位置 $A_{k}^2$，往后都是 $k - 2$ 种可能。

也就是钦定了 $2$ 个位置之后方案就确定了，于是一般情况也引刃而解了。

6/18

P1868 饥饿的奶牛 *普及+/提高

按右端点排序，树状数组优化。

P5020 [NOIP2018 提高组] 货币系统 *普及+/提高

猜想：$A$ 中不能被其他面值表示的 $x$ 一定属于 $B$。

证明：如果 $x \notin B$，一定有若干元素能凑出 $x$。在这若干元素当中，一定存在一个 $y$ 不能被 $A$ 中元素表示，否则 $A$ 能凑出 $x$，矛盾。

因为 $A$ 凑不出 $y$，$A, B$ 不等效。

有了这个结论就很好做了，按数值排序，第 $i$ 种面值只可能被 $i - 1$ 种表示。

如果能被表示，那么 $i$ 是多余的。否则保留 $i$。

P1005 [NOIP2007 提高组] 矩阵取数游戏 *提高+/省选−

行与行间独立。对于一个剩余区间 $[l, r]$，要么拿 $l$，要么拿 $r$，且当前在第 $m - len + 1$ 轮。

$f_{l, r}$ 表示从 $[l, r]$ 开始取到最后的最大值。$f_{l, r} = \begin{cases}2^{d} \cdot a_l + f_{l + 1, r}\\ 2^{d} \cdot a_r + f_{l, r - 1}\end{cases}$。

P3694 邦邦的大合唱站队 *提高+/省选−

算法一：枚举每个队伍的最终位置，预处理 $s_{i, j}$ 表示前 $i$ 个人里有多少个 $j$，时间复杂度 $O(m!m)$。

算法二：第 $i$ 只队伍只与前 $i - 1$ 只队伍是什么有关，而与其顺序无关。设 $f_{i, s}$ 为 $i$ 站在末尾，已经排完的队伍状态为 $s$ 的最小值，时间复杂度 $O(m^22^m)$。

算法三：第 $i$ 只队伍只与前 $i - 1$ 只队伍是什么有关，而与其末尾是什么无关，那么可以把 $i$ 的一维去掉，时间复杂度 $O(m2^m)$。

P3092 [USACO13NOV] No Change G *提高+/省选−

枚举硬币集合 $s$，求出 $s$ 所能到达的右边界 $f_s$。如果 $f_s = n$，则用不在集合内的总和更新答案。

P3572 [POI2014] PTA-Little Bird *提高+/省选−

$f_{i} = f_j + [h_i \ge h_j]$。

$i, j$ 间距可以单调队列维护。那么这个方程有没有单调性？

如果 $f_i = f_j$ 且 $h_i \ge h_j$，那么对于后续节点来说，$f_i$ 比 $f_j$ 更优。

也就是在维护间距的同时，对于相同的 $f$ 值取 $h$ 最大的一个。

此时队头元素一定是最小的且 $h$ 最大的，即便要加一，也不会劣于次大值。

P3089 [USACO13NOV] Pogo-Cow S *提高+/省选−

$f_{i, j} = v_i + \max(f_{j, k}),\ a_i - a_j \ge a_{j} - a_k$。

朴素会爆，可以二分 $k$，用树状数组优化成 $O(n^2\log n )$。

鉴定为不动脑子，考虑正常的 $O(n^2)$ 解法。

观察式子：$\begin{cases}f_{i, j} = v_i + \max(f_{j, k}) & a_k \ge 2a_j - a_i \\ f_{i - 1, j} = v_{i - 1} + \max(f_{j, k}) & a_k \ge 2a_j - a_{i - 1} \\\end{cases}$。

也就是在用 $f_{j, k}$ 更新 $f_{i - 1, j}$ 和 $f_{i, j}$ 时，随着 $i$ 的增大，$k$ 单调增减。

P4798 [CEOI2015 Day1] 卡尔文球锦标赛 *普及+/提高

直接数位 dp 的复杂度是 $O(n^3)$ 的，不能通过。

考虑试填法，枚举第 $i$ 个人的队伍 $j$：

$j = a_i$：继续考虑下一位。
$j < a_i$：后面随便填。

设 $f_{i, j}$ 表示共 $i$ 个人，第一个人$\le j$ 的合法方案。$f_{i, j} = (j - 1) \times f_{i - 1, j} + f_{i - 1, j + 1}$。（往队头加新元素）

那么这部分的方案为 $\sum f_{n - i, \max(j, mx) + 1}$，$mx$ 是前 $i - 1$ 个人的最大值。

CF976C *1500

左端点升序排序，左端点相同右端点降序排序，维护当前右端点最大。

CF33B *1800

floyd 求出任意字符转化的代价。枚举 $s_i, t_i$ 最后等于什么，取最小值。

CF819B *1900

维护 $a_i > i + k$ 的集合 $s$，$k$ 是当前移了几个到前面。

发现在 $s$ 内元素经一次操作会使答案减 $1$，不在 $s$ 内的会使答案加 $1$。

动态维护偏移量，单独处理当前末尾元素。

CF431E *2200

把修改离线下来，建值域线段树（因为不会动态开点）。

对于一个询问，二分最大值，把小于这个数的容器全部填满，看需要的水是否不小于他给出的水。

6/17

CF535D *1900

只要没有矛盾，空白位置随意填。否则答案为 $0$。

CF1249D2 *1800

扫描线，扫到 $i$ 时把 $l = i$ 的线段加入集合，把 $r < i$ 的线段踢出集合。

如果集合大小大于 $k$，把右端点最远的线段删掉，因为这样对后续影响最优。

AT_abc358_g *1698

最后一定是停在某个点不动。

如果你想走到当前点，一定是起点到当前点的简单路径，否则可以把环去掉更快的到当前点。

$f_{k, i, j}$ 表示走 $k$ 步到 $(i, j)$ 的最长距离。这里的 $k$ 最大取 $nm$，因为简单路径最长 $nm$。时间复杂度 $O((nm)^2)$。

Codeforces Round 953 (Div. 2)

D *1557

首先，初始排名最大的不需要删人。

如果编号为 $i$ 的人初始不是最大，必需要把 $1\sim i - 1$ 全部删掉，否则分数加不到他头上。

此时 $i$ 的总分为 $\sum_{i = 1}^n a_i$，检查这个数是否大于等于 $i + 1\sim n$ 的最大值。

如果成立，那么 $i$ 此时就是最大的，需要删 $i - 1$ 次。

否则还要把 $i + 1 \sim n$ 里最大的加到自己头上，需要删 $i$ 次。

E *2042

暴力怎么做？

贪心的用 $s$ 的 $0$ 使 $t$ 的 $1$ 先变多，再用 $t$ 的 $1$ 使 $s$ 的 $1$ 变多。
能影响 $s_i \to 1$ 的有效范围是多少？

$s_i$ 取决于 $t_{i - 1}$ 和 $t_{i + 1}$ 是否为 $1$。

$t_{i - 1}$ 取决于 $s_{i - 2}$ 和 $s_i$ 是否为 $0$，而 $s_{i - 2} = 0$ 只与原始序列有关。

因此 $s_i$ 的值只与 $[i - 2, i + 2]$ 有关。

我们不妨对整个 $s$ 操作变为 $s'$。

对于一个询问 $[l, r]$，$[l + 2, r - 2]$ 最后结果肯定是与 $s'$ 一致的。

然后再单独处理左右边界。

F *2518

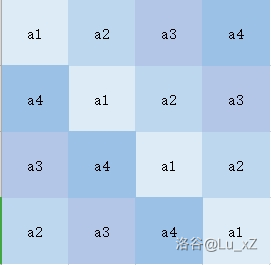
题目保证了 $k \ge 2$，所以对角线一定同属一个连通块。

所以只需要在 $2n - 1$ 条对角线间连边即可，元素个数由 $O(n^2)$ 骤减为 $O(n)$。

把对角线从左下到右上依次编号为 $b_1, \cdots_{b_{2n - 1}}$。不难发现，$b_i$ 与 $b_j$ 间的最短距离恰为 $\vert i - j\vert$。

因此，可以如下转化为序列上的问题。

接下来就很经典了。

枚举质因数 $p$，把包含 $p$ 的元素提出来，检查相邻两数的间距是否超过 $k$，并查集维护连通性。

注意特判 $a_i = 1$ 的情况，每个 $1$ 都是孤立点。

6/11

CF1362C *1400

分两类：奇偶，偶奇。偶奇的贡献始终为 $1$。奇偶的贡献为奇数从第 $0$ 位开始连续 $1$ 的长度加一。（$xxxx0111$ 贡献为 $4$）

枚举 $1$ 的个数，二分 $xxxx$ 的上界，复杂度 $O(\log^2 V)$。

更优秀的做法：答案等效于每位变化的次数。对于 $1011_2$，第 $0$ 位变化 $1011$ 次，第 $1$ 位变化 $101$ 次，以此类推。

CF802B *1800

贪心，每次删掉下一次出现时间最晚的节点。

CF725D *1800

先排序，记 $1$ 的初始名次为 $p_1$。维护一个优先队列，更容易飘走的放在堆顶。把原来就比 $1$ 大的加入队列，不断更新。如果 $1$ 比后面的小了，则把反超 $1$ 的元素加入队列。记飘走的人数为 $i$，反超的人数为 $j$，则用 $p_1 - i + j$ 更新答案。

CF893D *1900

维护当前持有金额的左右边界 $l, r$，初始为 $0$。询问时，$l = \max(l, 0)$，如果 $r < 0$，那么 $r \to d$，答案加一。

如果过程中出现 $l > d$，说明无解，如果 $r > d$，那么 $r = d$。

CF1083B *2000

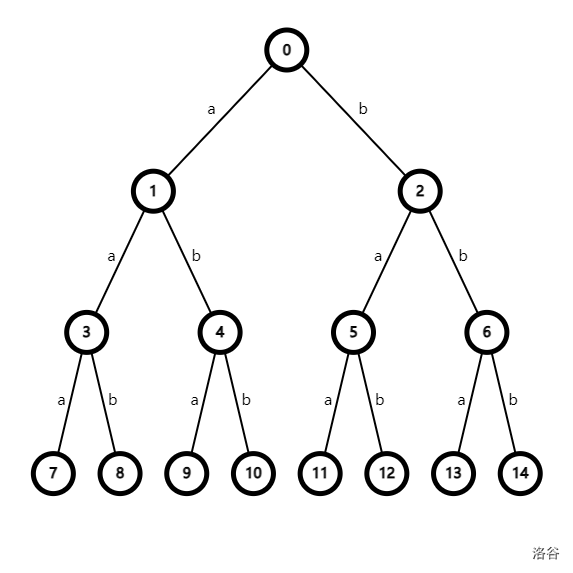
建满二叉树。$s, t$ 两个限制相当于左右两条路径把整棵树框起来。长度为 $i$ 的前缀相当于第 $i$ 层（0-base）的节点。

如果第 $i$ 层两条路径间的节点数小于 $k$，那么这些点全都要。否则，第 $i$ 层只能取 $k$ 个点，后续层数也只能 $k$ 个点（后续可不可能小于 $k$？）。

考虑证明下一层的合法节点不小于当前层。如果第 $i$ 层有 $n$ 个节点 $sxxxxt$，$s, t$ 分别有一个儿子，$x$ 有两个儿子，$2 + 2(n - 2) > n$。

CF486E *2200

线段树求出 $f_{i,0/1}$ 表示以 $i$ 结尾的 LIS 长即其方案数。同理可以求出以 $i$ 开头的长度和方案 $g_{i, 0/1}$。
记 $mx = \max(f_{i, 0}),\ tot = \sum[f_{i, 0} = mx]f_{i, 1}$。
如果 $f_{i, 0} + g_{i, 0} - 1 < mx$，说明不经过任意 LIS。否则如果 $f_{i, 1}\times g_{i, 1} = tot$，说明所有方案都经过 $i$。

方案数是指数级别。类似哈希思想，用两个大质数取模后比对。

CF650D *2600

对于修改 $(p, v)$，把子序列分为包含 $p$ 和不包含 $p$ 两部分。不包含 $p$ 的 LIS 是 $mx$ 还是 $mx - 1$ 取决于 $p$ 是不是必经点，可以用上题思路判断。

包含 $p$ 的部分，很容易想到用主席树在线做，但在本题是行不通的，空间消耗过大。（除非给你开到 2GB）

那么把询问离线即可。

CF1977D *2300

如果 $(i, j) = 1$ 且 $j$ 为特殊列，则行的操作序列确定。

枚举 $j$ 为特殊列，先记录把 $j$ 变为 00...00 的操作序列的哈希值 $H$。

采用异或哈希，第 $i$ 位的哈希值位 $h_i$，例如：10110 值为 $h_0\oplus h_2\oplus h_3$。

枚举 $(i, j) = 1$，则操作序列变为 $H\oplus h_i$。（$s_{i, j} = 0$ 则加上操作，$s_{i, j} = 1$ 则撤销操作）。

统计每个哈希值对应多少个列为特殊列，取最大的然后还原。

浙江广厦大学第七届程序设计比赛

幽默出题人。1e7 二分，1e6莫队，模 1e8 + 7。

6/12

CF1153C *1700

题目条件很好满足，只要让 $s_1$ 和 $s_n$ 匹配即可。问题转化为使 $s_2\sim s_{n - 1}$ 是合法括号序列，有两种方法。

法一：要填的 ( 数量确定，尽可能往前放。

法二：先令所有 ? 变为 )，维护 $cnt = \text{当前左括号数减右括号}$，如果 $cnt < 0$，看有没有变成 ) 的 ? 然后反悔。

CF1879D *1700

转化为前缀异或，按位计算。

只有 $s_{r, j} \ne s_{l - 1, j}$ 时，才有 $2^j \times (r - (j - 1))$ 的贡献。

如果 $s_{r, j} = 0$，记 $c_{1, j} = \sum\limits_{l = 1}^{r}[s_{l - 1, j} = 1],\ w_{1, j} = \sum\limits_{l = 1}^{r}[s_{l - 1, j} = 1] \times (l - 1)$，那么这一位的贡献为 $2^j\times (r \times c_{1, j} - w_{1, j})$。

CF666B *2000

预处理 $i \to j$ 的最短路 $d(i, j)$。我们要求一条 $a\to b\to c\to d$ 的路径。

枚举 $b$，那么 $a$ 为能到 $b$ 且 $d(a, b)$ 最大的点，否则不优。如果这个最大的点可以放到 $c, d$ 的位置，那么 $a$ 放次大点。以此类推，$a$ 的取值最多 $3$ 种。

枚举 $c$，可以事先把 $d(c, i)$ 排序，那么可以循环不超过 $4$ 次就找到不与 $a, b$ 相同且最大的 $d$。

时间复杂度 $O(n^2)$。

Ac371.牧师约翰最忙碌的一天

令第 $i$ 人举办婚礼的状态为 $x_i$，在前一段时间的表示为 $x_i = 0$，后一段为 $x_i = 1$。

如果 $i$ 在 $0$ 办与 $j$ 在 $0$ 办的时间冲突，等效于条件 $\neg [x_i = 0] \lor \neg[x_j = 0]$。

如果 $i$ 在 $0$ 办与 $j$ 在 $1$ 办的时间冲突，等效于条件 $\neg [x_i = 0] \lor \neg[x_j = 1]$。同理剩下两种情况。

Codeforces Round 952 (Div. 4)

$d(kn) = kd(n)$ 成立当且仅当 $n$ 乘 $k$ 后不进位，证明待补。

记 $x = \lfloor\dfrac{9}{k}\rfloor$。对于一个长度为 $i$ 的数字 $n$，最高位 $\in [1, x]$，剩余位 $\in [0, x]$，总个数为 $(x - 1)x^{i - 1}$。

符合条件的数字长度 $\in [l + 1, r]$。则合法数字个数为 $(x - 1)(x^l + \cdots + x^{r -1}) = x^r - x^l$。

只考虑行，列同理处理。

定义行 $i$ 的额外贡献 $r_i$ 为不属于 $i$，但把 $i$ 涂黑后属于一个连通块的节点数量。

对于一个大小为 $g$ 的连通块 $G$，会对所有贯穿 $G$ 的行以及与 $G$ 相邻的行产生额外贡献。

$r_i = g - cnt_x(i)$，$cnt_x(i)$ 表示属于 $G$ 且横坐标为 $i$ 的节点数量。

最后答案为 $m + \max(r_i)$。

和 H1 思路一致。

设 $G$ 对行 $i$ 的额外贡献为 $r_i$，列 $j$ 的额外贡献为 $c_j$。

把 $i, j$ 染色后的连通块大小是否为 $n + m - 1 + r_i + c_j$？

如果一个 $G$ 同时对 $i, j$ 产生了额外贡献，应当被记入答案的贡献为 $g - cnt_x(i) - cnt_y(j) + cnt_{xy}(i, j)$，实际记入 $(g - cnt_x(i)) + (g - cnt_y(i))$。

重复计算了 $g - cnt_{xy}(i, j)$。

枚举 $G$ 产生贡献的行 $i$ 列 $j$，把 $g - cnt_{xy}(i, j)$ 加入 $rc_{i, j}$ 表示 $i, j$ 重复计算的个数。

连通块大小是 $\sum g = O(nm)$ 的，而有贡献的 $i \times j = (\text{连通块的行数 + 周围一圈}) \times (\text{连通块的列数 + 周围一圈}) = O(?)$，所以总复杂度 $O(?)$。

最坏复杂度 $O(n^3/6)$，可以恰好通过。

6/13

CF1292B *1700

本身距离大于 $t$ 的不可选。剩下的点只有 $\log V$ 级别，横纵坐标增长系数大于一，点的连线是单调递增的。

要选的点一定是段连续区间，枚举始末位置即可。（函数是单调的，始末位置相减就是答案）

CF958C2 *2000

朴素 $O(n^2k)$ dp 很好想，$f_{i, k} = f_{j, k - 1} + (s_i - s_j) \bmod p$。

用题目中有明显暗示的 $p \le 100$ 去优化。

$(s_i - s_j) \bmod p$ 只与 $s_j \bmod p$ 有关，利用这一点可以省去枚举 $j$ 的步骤。

$f_{x, k}$ 表示前缀和模 $p$ 等于 $x$ 的前缀分成 $k$ 段的最大值，$f_{x, k} = f_{y, k - 1} + (s_i - y) \bmod p$，复杂度 $O(npk)$。

CF958C3 *2500

朴素方程：$f_{i, k} = \min(f_{j, k - 1} + (s_i - s_j) \bmod p)$。

假设 $f_{i, k}$ 分别从 $f_{x, k - 1}, f_{y, k - 1}$ 转移来，满足 $f_{x, k - 1} \le f_{y, k - 1}$ 。

$f_{i, k}$ 可以取 $f_{x, k - 1} + (s_i - s_x) \bmod p$ 或 $f_{y, k - 1} + (s_i - s_y) \bmod p$。

我们让前项减后项：$d = (f_{x, k - 1} - f_{y, k - 1}) + (s_i - x) \bmod p - (s_i - y) \bmod p \le 0 + p - 1 + 0\le p - 1$。

无论从那边转移过来 $f_{i, k} \equiv s_i \pmod p$，因此有 $p \mid d, d \le 0$。

说明从 $x$ 转移不会比 $y$ 更劣。记录每个 $k$ 对应的最小值即可 $O(1)$ 转移。

CF1237D *2000

$2\min(a) \ge \max(a)$ 则一直不会停。如果从 $i$ 开始，第一个小于 $a_p/2$ 的位置 $j$，那么 $i\sim p$ 的所有位置（出发）都会在 $j$ 停下。

单调队列维护，由于有的位置要跑两轮才会结束，所以原数组要复制 $3$ 遍。

CF1971H *2100

$+ 1$ 视为真，$-1$ 视为假。条件 $(x_1\land x_2) \lor (x_1 \land x_3) \lor (x_2 \land x_3) \iff (x_1\lor x_2) \land (x_1 \lor x_3) \land (x_2 \lor x_3)$。

CF27D *2200

设一条路的状态为 $x_i = i/o$，如果 $i, j$ 相交，需要满足 $(x_i = i \lor x_j = i)\land (x_i = o \lor x_j = o)$。

CF1239D *2400

一个点要么选人，要么选猫（当然不能同时选），人猫缩成一个点。对于限制条件 $(x, y)$，$x\to y$ 表示 $x$ 选人则 $y$ 不选猫。

在同一个强连通分量的点要么全人，要么全猫。让一个没有出边的 scc 全是人，剩余全是猫即可构造解。

（为什么不要拆成 0/1 点？如果拆点，连的边为 $x_0\to y_0$, $y_1\to x_1$，两个完全相同的子图相互独立）

UVA11294

模板题，题意比较刺激。一对夫妻拆成 $4$ 个点。

UVA1391

每个宇航员只有两种选择。如果发生冲突的 $i, j$ 原本属性一致，那么必须一个选 $C$，一个选原来的；否则只要满足有一个选原来的。

P3007 [USACO11JAN] The Continental Cowngress G

在拓扑图上：如果通过的点是驳回点的严格后继，必须选通过；如果驳回点是通过点的严格后继，必须选驳回；否则都可以。

6/14

P3513 [POI2011] KON-Conspiracy

对于一个可行解而言（$0$ 为后勤，$1$ 为同谋），$x$ 与其相邻的点 $y$ 满足 $(x = 0) \lor (y = 0)$ ，与其不相邻的点 $y'$ 满足 $(x = 1)\lor (y' = 1)$。

因此我们可以用 2-sat 构造出一组可行解，把原点集分为后勤 $A$ 和同谋 $B$。

考察用这一组解推出全部解。两种方法：交换；移动。

如何才能交换一个 $x\in A$ 和 $y\in B$？设 $x$ 在 $B$ 中会产生矛盾的点的数量为 $b_x$，$y$ 在 $A$ 中产生矛盾的点数为 $a_y$。

$b_x = 0$ 或 $b_x = 1$ 且恰为 $y$。
$a_y = 0$ 或 $a_y = 1$ 且恰为 $x$。

最多把 $A$ 中一个点拿到 $B$，否则原 $A$ 中两点会在 $B$ 产生矛盾。反之同理。

如何才能把 $x\in A$ 拿到 $B$？$b_x = 0$。

移动完的方案要不要再交换？由于最多一个跑到对面，交换的合法情况一定被包含在移动里了。

P3825 [NOI2017] 游戏

没有 x，就是朴素 2-sat。把 x 等效为 a 或 b 即可包括所有情况，发现 $d$ 很小，$2^d$ 枚举。

CF992D *2100

如果乘的数非 $1$，循环 $O(\log)$ 次就爆了，可以直接枚举。

否则对于一段连续的 $1$，乘积恒定不变，总和单调递增，最多产生 $1$ 的贡献。

CF1615C *1600

对 $i, j$ 分别执行一次操作。若 $i = j$，原序列不变。否则满足 $a_i = 1, a_j = 0$ 且操作后其余位置保持不变，$a_i = 0, a_j = 1$。

又由于两次操作不会使序列当中 $1$ 的数量改变，相当于把不在位置上的 $1$ 移到了该在的位置。

如果原序列中 $a, b$ 所含 $1$ 的数量相同，答案即两串中不同位置的数量 $d$。（一定是偶数，一个 $1$ 不在位置上，必定有一个 $0$ 不在位置上）

如果操作奇数次呢？

可以先把 $a$ 操作一次转化为偶数次。我们要最小化操作后的不同位置数 $+1$。

如果 $a', b$ 所含 $1$ 相同：选 $a_i = b_i$ 翻转，翻转后 $n - d + 1$ 个位置不同；选 $a_i \ne b_i$ 翻转，翻转后有 $n - d - 1$ 个位置不同。

一定存在一个 $a_i = 1, b_i = 0$，否则两串完全相同。

CF1584F *2600

$O(m^24^n)$ 暴力转移，$m$ 为串长：$f_{i, ss}$ 表示以 $s_i$ 结尾，状态为 $ss$ 的 LCS。其中状态 $ss$ 表示 $s_i$ 在各个串中的位置， $0/1$ 分别代表第一/二个位置。

需要满足什么条件才能从 $f_{j, tt} + 1$ 转移？在 $tt$ 的意义下，所有 $s_j$ 的位置严格小于 $s_i$ 在 $ss$ 下的位置。

优化转移：贪心将 $f_{i, ss} + 1$ 转移到符合条件且 $tt$ 最小的 $f_{j, tt}$，因为越靠前越优（且每一位独立），时间复杂度 $O(m^2n2^n)$。

（实际上可以把转态设为 $f_{ch, ss}$，直接枚举字符，记搜转移，可以省去 $4$ 倍常数）

CF24D *2400

设 $f_{i, j}$ 表示 $(i, j)$ 到第 $n$ 行的期望步数。

\[f_{i, j} = \begin{cases} \frac{1}{3}f_{i, j} + \frac{1}{3}f_{i, j + 1} + \frac{1}{3} f_{i - 1, j} + 1 & j = 1\\ \\ \frac{1}{3}f_{i, j} + \frac{1}{3}f_{i, j - 1} + \frac{1}{3} f_{i - 1, j} + 1 & j = m\\ \\ \frac{1}{4}f_{i, j} + \frac{1}{4}f_{i, j - 1} + \frac{1}{4}f_{i, j + 1} \frac{1}{4} f_{i - 1, j} + 1 & \texttt{otherwise} \end{cases} \]

每行可根据下一行推出，联立 $m$ 个 $m$ 员方程组，$O(m)$ 消元，$O(m)$ 回代。

牛客小白月赛96

质量很高的一场，F 脑抽了。

B：全 $0$ 全 $1$，$0$ 次；$0/1$ 数量不等，$1$ 次；$0/1$ 数量相等，如果长度只有 $2$，无解，否则两次（找到一个 $0/1$ 不等的前缀）。

C：枚举 $i$，$j$ 单调不减。

D：把权值为奇的点叫做奇点，权值为偶叫偶点。

$a, b < 0$，连一张完全图。
$a< 0，b > 0$，如果同时存在奇偶点，连两张完全子图，再在奇图和偶图间连一条 $b$；如果只有一种点，$b$ 不要连。
$a > 0,\ b < 0$，如果同时存在奇偶点，只连 $b$ 边且保证联通；否则连一条包含 $n - 1$ 个 $a$ 的链。
$a, b \ge 0,\ a < b$，如果同时存在奇偶点，链两条 $a$ 链，再用 $b$ 边联通；否则只有一条 $a$ 链。
$a, b \ge 0,\ a > b$，如果同时存在奇偶点，一个只含 $b$ 边的树；否则只有一条 $a$ 链。

E：第一次扫描求出 $f_i$ 表示以 $i$ 为根的子树中的支撑点个数以及 $up_x, down_x$。

第二次扫描，求出删掉 $x$ 为根的子树后的支撑点个数。

记 $x$ 的父亲为 $fa$。

如果 $y$ 在 $fa\to 1$ 的链中，且 $up_y \ge a_y \land dw_y > a_y$，说明这个点没被用过且有可能产生答案。

如果 $down_x + a_x \ge dw_y - a_y$，则 $y$ 记入答案。

把 $x$ 删掉后 $fa$ 一定能记入答案，先加入，然后继续往下递归，考虑要不要反悔。

用堆维护，一个点最多反悔一次，时间复杂度 $O(n\log n)$。

F：$[a_1, a_2, \cdots,a_i]\to [a_1, a_2, \cdots,a_i]$，逆序对数要加 $1\sim i$ 中大于 $a_1$ 的个数，减 $1\sim i$ 中小于 $a_1$ 的个数，预处理后可 $O(1)$ 更新。

对于每个前缀枚举 $i$ 种情况，总复杂度 $O(n^2)$。

6/7

CF1561D1/2 *1700/1900

D1：$f_n = \sum\limits_{i = 1}^{n - 1}f_i + \sum\limits_{i = 2}^{n}f(\lfloor\dfrac{n}{i}\rfloor)$，前缀和 + 整除分块，$O(n\sqrt n)$。

D2：算 $f_i$ 对后续 $f_j$ 的贡献。1. 所有 $j > i$。 2. $f_{ki}, f_{ki + 1},\cdots f_{ki + k - 1}$。差分 + 调和级数枚举 $O(n\log n)$。

CF1619G *2000

合并可以连续引爆的点，以连通块内最小时间为键降序排序，从 $0$ 开始枚举时间 $i$，如果 $i \ge t_i$，则答案为 $\min(i - 1, t_i)$。

如果没有 $i \ge t$，答案为连通块数减一。联通块求法：枚举横坐标，先同一横坐标内合并，再枚举有相同纵坐标的左边的点。

CF264C *2000

朴素 dp，$f_i = \max \begin{cases}f_j + a \times v_i&c_j=c_i\\\max(f_j, 0) + b \times v_i&c_j\ne c_i\end{cases}$，按颜色建线段树，支持区间最大。upd：喜报，线段树 T 了。

转移来源只有两部分，第一部分很好维护，第二部分维护最大值和次大值，要求两值颜色不同，根据当前颜色转移。

Codeforces Round 951 (Div. 2)

B *949

如果 $[l, r] \oplus x= [l', r'] \oplus y$，则 $[l, r]= [l', r'] \oplus(x\oplus y)$。

令 $v = (x\oplus y)$，即求最长的 $[l, r]$ 使得异或上 $v$ 后依然连续。

如果 $v = abc100000$，任意 $l = a'b'c'100000, r = a'b'c'111111$ 一定是合法且最长的，长度为 $\text{lowbit}(v)$。

C *1201

设最后共用 $S$，如果第 $i$ 个结果押 $a_i$，满足 $a_i > \dfrac{S}{k_i}$，两边求和得到 $S > S (\sum\dfrac{1}{k_i})$。

如果不满足这个条件，一定无解。否则 $S$ 任取，为了避免精度问题，取 $S = \text{lcm}(k_i)$。

D *1831

只有一段连续区间的末尾可以作为分割点（红蓝交界），符合要求的位置少于 $\dfrac{n}{k}$ 个。

预处理 $pre_i$ 表示 $s_1\sim s_i$ 的翻转是否合法，$suf_i$ 表示 $s_i\sim s_n$ 是否合法。

如果 $pre_p = 0$ 或 $suf_{p + 1} = 0$，则一定不合法。

否则，检查每个 $i \in [\max(p + 1, n - k + 1), n]$，是否满足 $s_{i} \ne s_{p - (i + k - n) + 1}$，即后缀与翻转后的前缀之间是否合法。

每个位置最多检查 $k$ 次，时间复杂度 $O(n)$。

E *2419

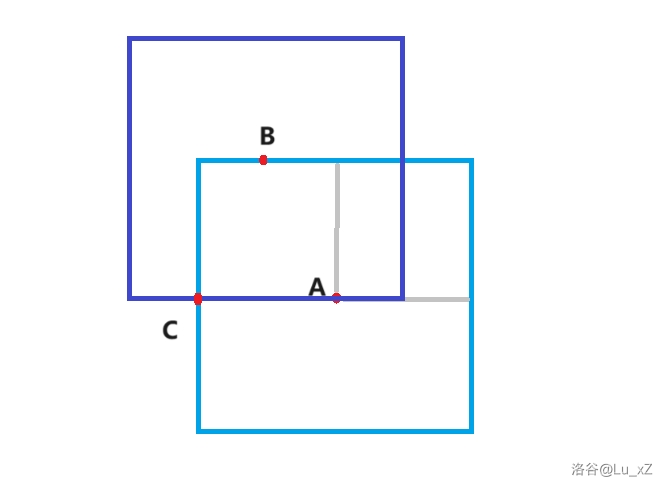
曼哈顿转切比雪夫。枚举点 $A$，则 $B$ 在以 $A$ 为中心，边长为 $2d$ 的正方形上。

$C$ 需要同时满足 $A, B$ 两个限制。可以发现，$C$ 的取值是唯一的，且其横坐标和纵坐标中一定有一项与 $A$ 相同。

枚举横坐标 $x$，如果存在两点 $x_i = x_j = x, \vert y_i - y_j\vert = d$，分别检查 $x_k = x + d$ 或 $x - d$ 的点中是否存在 $y_k \in [y_i, y_j]$。

同理可以枚举纵坐标。

牛客练习赛126

非常好 C 8dirt，使我的 rating 减 60。

$g(n) = \gcd(\dfrac{n(n - 1)}{2}, \dfrac{n(n + 1)}{2}) = \begin{cases}n & n \equiv 1\bmod 2\n / 2&n\equiv 0 \bmod 2 \end{cases} $，$f(n) = f(n - 1) + g(n)$ 等差数列求和。

离散化。考虑每个 $a_i$ 作为最小值的可行左右端点 $l_i, r_i$，满足 $\forall j \in [l_i, r_i],\ a_i \le a_j$，单调栈维护。

计 $mx_i$ 表示最小值为 $\ge i$ 的最大长度，$1\sim n$ 扫一遍再取后缀 $\max$。对于每个询问检查是否 $mx_v\ge l$。

单调栈维护 $l_i, r_i$ 使得 $\forall j \in [l_i, i), a_i \le a_j$，$\forall j \in (i, r_i) a_i < a_j$。这样可以保证对于$l \in [l_i, i], r \in [i, r_i]$，$a_i$ 是 $[l, r]$ 内最右侧的最小值，防止区间重复计算。

离线每个询问和修改，从大到小扫描， $v = a_i$ 时加入 $l \in [l_i, i], r \in [i, r_i]$ 的贡献。

线段树维护每种长度的方案数，设当前长度为 $i$ 的子数组有 $t_i$ 个。

对于一个修改 $(L, R, p$)，$l, r$ 分别属于 $[L, p], [p, R]$，记 $len = len(l, r), x = len(L, p), y = len(R, p)$，如果 $x > y$，交换 $x, y$。

考虑每种长度的数组个数：

$len < x$，$t_{len} \to t_{len} + len$。
$len \in [x, y]$，$t_{len} \to t_{len} + x$。
$len> y$， $t_{len} \to t_{len} + (R - L - len + 2)$ 。

上述操作都可转化为 $add(l, r, st, d)$： $\forall i \in [l, r], t_i \to t_i + st + (i - l) \times d$。（区间加一个等差数列）

设 $b_i$ 为 $t$ 的差分数组，则 $add$ 操作转化为：$b_l$ 加首项，$b_{l + 1}\cdots b_{r}$ 加公差，$b_{r + 1}$ 减去末项，线段树很容易做到。

对于一个询问 $(v, l, r)$，查询 $\sum_{i = l}^r t_i$。

由于我们只维护了差分数组，不能直接算，$\sum_{i = 1}^rt_i = \sum_{i = 1}^r\sum_{j = 1}^ib_j = \sum_{j = 1}^r b_j \times (r - j + 1) = \sum_{i = 1}^r b_i \times (r + 1) - \sum_{i = 1}^r b_i \times i$。

所以只要再维护个 $b_i \times i$ 就好了。

6/8

CF1056B *1600

求 $\sum_{i = 1}^n\sum_{j = 1}^n[i^2 + j^2\equiv 0\pmod m]$。枚举 $i, j$ 的剩余类，再计算 $1\sim n$ 有多少与 $x$ 同余的数 $f(x) = \lfloor\dfrac{n}{m}\rfloor + [x \land x \le n \% m]$。

CF1575K *2200

如果两个矩形相同，答案为 $(nm)^{k}$。否则，随便填其中一个矩形的非重合部分，剩下部分唯一确定，方案数 $(nm-rc)^k$。

【LGR-189-Div.2】核桃编程 6 月月赛 I & JRKSJ Round 8

1 + 2 场，还是太菜。

神秘结论题（甚至只是猜想），$2$ 的非负整次幂中只有 $65536$ 不含 $1, 2, 4, 8$。把原串中 $1, 2, 4, 8$ 都改掉，单独计算 $65536$。

$s_x = (,\ s_y = )$。
$x, y$ 在 $G$ 中联通。
路径长一定为偶数。等效于找到一条 $x$ 的奇点到 $y$ 的偶点的路径。具体的讲，对于边 $(x,y)$，$x$ 连向 $y'$，$x'$ 连向 $y$。

考虑特殊情况，只在 ( 和 ) 间连边。设新图为 $H$，如果 $x$ 和 $y'$ 在 $H$ 中联通，则存在路径 ()()...()()。

一般的，如果 $x$ 和 $y'$ 在 $G$ 中联通，考虑第一次出现的 (( 和最后一次出现的 ))，即 ()()...((......))...()()。（一定会同时出现 (( 和 ))，否则不可能匹配）。由于不一定是简单路径，可以在两点反复横跳，不断增加 (( 数量，如 ()()...(( (( (( ...。

双括号 ((......)) 中间不断匹配剩下的一定形如 ...)))(((... 且长度为偶数（因为总长度为偶数）。

不论剩下的序列是奇数还是偶数个 )，都可以不断增加两侧的双括号消去。

于是将问题转化为：是否能从 $x$ 在 $H$ 中走到一个点 $u$，满足 $u$ 在原图中有一条 (( 边，且可以从 $y'$ 走到 $v$，满足 $v$ 有 )) 边。

这样是一定能构造的：$x\xrightarrow{H} u \xrightarrow{H} x \xrightarrow{G} y' \xrightarrow{H} v \xrightarrow{H} y'$，长度为偶数。

AtCoder Beginner Contest 357

最懂罚时的一集。

C：分治。

D：设 $q$ 为严格大于 $n$ 的 $10$ 的整数幂，那么答案为 $q(\cdots q(qn + n) + n\cdots) + n$，展开得到 $n(1 + q + \cdots + q^{n - 1})$。

E：缩点，$f_x = sz_x^2 + \sum\limits_{(y, x) \in E} f_y \times sz_x$。

F：线段树维护 $\sum A, \sum B, \sum A \times B$ 和 $A, B$ 各自懒标记。

Leetcode 第 132 场双周赛

2：模拟完一轮后最大值就待在队首不动了，不需要考虑移到队尾的元素。

3，4：把 cf264c 拓展到二维。$f_{i, k} = \max \begin{cases}f_{j, k} + 1&a_j=a_i\\f_{j, k - 1} + 1&a_j\ne a_i\end{cases}$，第一部分维护 $g_{c, k} = \max(f_{j, k}),\ (j < i\land a_j = c)$。

第二部分维护 $mx_{0, k}$ 和 $mx_{1, k}$ 分别为最大值和次大值，且两值颜色不同，$f_{a_i, k} = \begin{cases}mx_{0, k - 1} + 1& mx\_color_{0, k - 1}\ne a_i\\mx_{1, k - 1} + 1&\text{otherwise}\end{cases}$。

6/9

牛客周赛 Round 46

MyGo 场。没无伤 ak 是因为 f 取模取错了（

D：$\text{mex}$ 的取值只可能 $0, 1, 2$，分类讨论。或许有更优雅的做法。

E：如果数量小于 $k$，贡献为 $a_i \times b_i$，否则为 $a_i \times q$。

F：设 $n = \prod p_i^{a_i}$，相当于把 $a_i$ 个 $p_i$ 分配给 $x_1, x_2, \cdots, x_y$，答案即 $\prod\begin{pmatrix}a_i + y - 1\\y - 1\end{pmatrix}$，暴力算 $ \begin{pmatrix}a_i + y - 1\a_i\end{pmatrix}$。

Codeforces Global Round 26

如果 $a_1 = a_n$，无解。

如果 $a_2 = a_n$，$a_1, a_2$ 涂成红色，否则只把 $a_1$ 涂成红色。

如果首位不等于 $1$，无解。

否则可以推出两个数 $a + b = x$ 每一位的和，且这个和一定属于 $[10, 18]$，否则无解。

例如：$1393938$。

$a_0 + b_0 = 18$。
$a_1 + b_1 = 13 - 1$（一定有进位）。
$a_2 + b_2 = 19 - 1$。

以此类推。

最多只会用一次操作二。

反证法，考虑最后两次操作二分别对应 $c + a_i$ 和 $c + a_j$。显然 $c + a < 0$ ，否则没必要用操作二。如果 $i$ 处用了操作 $1$ ，$c + a_j$ 将变得更小，从而使答案增大。

维护最小前缀和 $x = \min(s_i, 0)$，则最终的 $c = s_n - 2x$。

延续 C1 的思考方向。

如果 $x = 0$，操作中不出现负数。因此操作一操作二是等效的，方案数为 $2^n$。

如果 $s_i = x$，说明可以在这一步进行操作二达到最终的 $c$。

记 $k = \sum\limits_{j <i}[s_j\ge0]$，表示在 $i$ 之前有 $k$ 步可以用两种操作。因为 $c \ge 0$，所以在 $i$ 之后的所有的操作都是非负的，贡献为 $2^k \times 2^{n - i}$。

设 $s$ 长度为 $n$。特判全为 a 的情况，共 $n - 1$ 种方案。

设 $s$ 中非 a 字符的数量为 $m$。

如果 $t$ 中有 $k$ 个非 a 字符，把 $t$ 掐头去尾忽略前后的 a 后，原串里一定恰好存在 $\dfrac{m}{k}$ 个 $t'$，且 $k\mid m$。

枚举 $k$。记录第 $i$ 个非 a 字符的位置为 $p_i$（从 $0$ 开始），如果 $s_{p_i} \ne s_{p_i - k}$ 或不在分割处的 $p_i - p_{i - 1}\ne p_{i - k} - p_{i - k - 1}$，$t'$ 不合法。

把 $t'$ 还原为 $t$，枚举左边有的 a 个数 $l \in [0, p_0]$。

设 $x$ 为分割处的最小间隔 $\min(p_i - p_{i - 1}),\ k \mid i$，则右边的 a 个数 $r \in [0, \min(x - l, n - p_{m - 1} - 1)]$。

把一个点的父亲儿子都加到 $T_2$ 后，这个点就是叶子，且与之直接相连的点都不是叶子。（所有相邻点都是这个点的祖先）。

所有的叶子构造一个独立集，我们找去除根后最大的，类似 上司的舞会。

枚举每个节点作为初始的根，换根 dp。如果根本身就是叶子还要在加一。

具体来说，第一次扫描以 $1$ 为根求出 $f_{x, 1/0}$ 表示以 $x$ 为根的子树中 $x$ 选/不选的最大独立集：$\begin{cases}f_{x, 0} = \sum_{y \in g_x} \max(f_{y, 0}, f_{y, 1}) \\ f_{x, 1} = \sum_{y \in g_x} f_{y, 0}\end{cases}$。

第二次扫描求出 $h_{x, 1/0}$ 表示选/不选 $x$ 的最大独立集，$h_{1, 0/1} = f_{1, 0/1},\ \begin{cases}h_{x, 0} = \max(h_{fa, 1},\ f_{x, 0} + (h_{fa, 0} - \max(f_{x, 1}, f_{x, 0})))\\h_{x, 1} = f_{x, 1} + (h_{fa, 0} - \max(f_{x, 1}, f_{x, 0})) \end{cases}$。

用 $h_{x, 0} + [x \texttt{ is leaf}]$ 更新答案。

待补。

6/10

CF1364B *1300

往序列里增加元素对答案的影响只增不减。不妨一开始全选，删除递增/减段，只保留转折节点。

CF1461D *1600

顺序无所谓，先排序。预处理所有可能的值，最多递归 $\log n$ 层。

CF1286B *1800

理想的方案是 $1\sim n$ 分配给每个点。

当我们已经分配完 $x$ 的子树后，将子树中的点按值排序并将 $x$ 插入，重新分配 $1\sim sz_x$。这样不会产生矛盾，因为子树之间互不影响。

CF524C *1900

？暴力题。值域很大，数量很小，枚举两种数各有多少，复杂度 $O(nk^3)$。

CF1974E *1800

1800？1500！$\sum h_i$ 很小，可以作为状态。相当于把背包问题的价值和体积颠倒。

CF551D *2100

按位考虑。如果 $k_i = 0$，$\{a\}$ 中不存在相邻的两个数第 $i$ 为 $1$。

$\begin{cases}f_{x, 0} = f_{x - 1, 0} + f_{x - 1, 1}\\f_{x, 1} = f_{x - 1, 0}\end{cases}$，写成矩阵乘法：$\begin{pmatrix}f_{n, 0}\\f_{n, 1}\end{pmatrix} = \begin{pmatrix}1&1\\1& 0\end{pmatrix}\begin{pmatrix}f_{{n - 1}, 0}\\f_{{n - 1}, 1}\end{pmatrix}$。

要求 $f_{n, 0} + f_{n, 1} = f_{n + 1, 0}$ 即求 $ \begin{pmatrix}1&1\1& 0\end{pmatrix}^{n + 1}\begin{pmatrix}1\0\end{pmatrix}$。如果 $k_i = 1$，用 $2^n$ 减去 $0$ 的方案即可。

CF802B *1800

6/3
CF1498C *1600

设 $f_{i, j}$ 表示一个前面有 $i$ 个挡板，能量级为 $j$ 的粒子最终分裂成多少个，$f_{i, j} = \begin{cases}f_{i - 1, j} + f_{n - i, j - 1}\\1 \quad i = 0\land j > 0\end{cases}$。

CF802K *2100

$f_{x, 0}$ 表示从 $x$ 出发且回到 $x$ 的最大值，$f_{x, 1}$ 表示从 $x$ 出发不回到 $i$ 的最大值。

$f_{x, 0}$ 最多选 $k - 1$ 个儿子，且每个儿子 $y$ 的贡献是 $f_{y, 0}$。

$f_{x, 1}$ 最多选 $k$ 个儿子，有且只有一个儿子是 $f_{y, 1}$。

模拟赛（上午）：

T3：二分答案，$\forall i \in [1, n]. s_{i - 1} - s_i <= 0,\ s_i - s_{i - 1} <= 1,\ s_{n} - s_0 \le mid ,\ s_{0} - s_{n} \le -mid,\ \begin{cases}s_{l - 1} - s_r \le -k & v = 0\\s_r - s_{l - 1} \le mid - k & v = 1 \end{cases}$，建图，spfa 判负环。

T4：每天必须打一个，一旦能打过就一直能打过，dij 求出每个点最早能被打败的时间 $t_i$ ，把城市 $2\sim n - 1$ 分配给 $1 \sim t_n - 1$ 的每一天（按 $t$ 从小到大），如果存在某天 $i < t$ 或城市不够则无解。

CF1976：

B：每次操作一定是 $a_i\to b_i$ 或 $b_i\to a_i$，维护所有区间 $[a_i, b_i]$ 与 $b_{n + 1}$ 间的最短距离 $mi$，答案为 $1 + mi + \sum\mid a_i - b_i\mid$。

C：维护两种工作各自被强迫去另一种的第一人，算贡献时分讨即可。

D：$'('\to 1, \ ')'\to -1$，计算字符串 $t$ 的前缀和 $s$，一个括号序列能够完美匹配当且仅当 $\forall s_i\ge 0$ 且 $s_n = 0$。

如果翻转 $[l, r]$ 且仍要维护上述性质，必须满足 $s_r = s_{l- 1}$ 且 $\forall i \in [l, r],\ s_{l - 1} - (s_i - s_{l - 1}) \ge 0$，第二个条件移下项即 $2s_{l - 1} > s_i$。

把 $s$ 值相同的位置拎出来，钦定某个位置为 $l - 1$，二分右端点，随便写个支持 rmq 的东西 check。

E：（待补）

F：（待补）

CF1981：

A：$2l < r \to \log_2 l + 1 < \log_2r\to 2^{\lfloor\log_2r\rfloor} \in [l, r]$，所以答案就是 ${\lfloor\log_2r\rfloor}$。

B：设 $L = \max(0, n - m), R = n + m$，即求 $L \mid L + 1\mid \cdots\mid R$，依次检查第一个 $\ge L$ 且第 $i$ 位为 $1$ 的数是否 $\le R$。

C：如果 $l, r$ 确定，$(l, r)$ 都不确定，即找到一种方案使 $a_l$ 通过 $\times 2,\ \times 2 + 1,\ /2$ 变成 $a_r$，上述操作等价于在 $a_l$ 后面加 $0$，加 $1$，左移 $1$。

那么 $l, r$ 间（不带重复）的唯一路径即满二叉树上 $a_l$ 到 $a_r$ 的路径，检验路径长与区间的奇偶性，然后不断乘二除二。

D：必要条件：对于任意 $i \ne j$ ，无序对$(a_i, a_{i + 1}) \ne(a_j, a_{j + 1})$，如果所有数都是质数，则变为充要条件。

$a_i$ 连向 $a_{i + 1}$，题目等价于在 $m$ 个点的无向完全图（算上自环）中找到一条不小于 $n$ 的路径，满足每个点都是质数且每条边只经过一次。

计 $f(m)$ 表示前 $m$ 个质数能构造出打最长路径长。

当 $m$ 为奇数时，$\forall i$ 度数为偶（$m + 1$），存在长为 $f(m) = \dfrac{m(m + 1)}{2} + 1$ 的欧拉路径。
当 $m$ 为偶数时，$\forall i$ 度数为奇，考虑删边，删一条边最多使两个点的度数变为偶，考虑删 $(2, 3), (4, 5), \cdots, (m - 2, m - 1)$，只剩 $1$ 和 $m$ 为奇。

存在 $1$ 到 $m$ 的欧拉路径满足 $f(m) = \dfrac{m(m + 1)}{2} -(\dfrac{m - 2}{2}) + 1 = \dfrac{m^2}{2} + 2$，在 $m$ 个点的图上一定是最长的。

那么函数 $f$ 是否有单调性呢？

$m$ 为偶数：$f(m) - f(m - 1) = \dfrac{m}{2} + 1 > 0$，$m$ 为奇数：$f(m) - f(m - 1) = \dfrac{3(m - 1)}{2} > 0$，单调递增。

二分 $m$，跑欧拉路径。

6/4

模拟赛（上午）：（扫描线场（？

T1：翻转两次等于不翻转，计 $r(i) = v, v\in \{0, 1\}$ 表示第 $i$ 行的状态，同样定义 $c(i)$。$(i, j)$ 为黑当且仅当 $r(i) \oplus c(j) = 1$

对于行 $l_1\sim r_1$，列 $l_2\sim r_2$，总贡献为 $cnt\big(r(i) = 1\big) \times cnt\big(c(j) = 0\big) + cnt\big(r(i) = 0\big) \times cnt\big(c(j) = 1\big)$，线段树维护区间翻转。

T2：扫描线，分别计算每个时刻数轴上值为奇数和偶数的点的个数。

T3：dfs 序转化为序列问题，正难则反，用 $n^2$ 减去不合法情况。

考虑限制条件 $(u, v)$，贡献为 $i \in [in_u, out_u]m,\ j \in [in_v, out_v]$ 的 $(i, j)$ 对（或 $(j, i)$），抽象到平面上以 $(in_u, in_v)$ 和 $(out_u, out_v)$ 为对角的矩形面积。

矩形面积并，注意一组限制条件对应一横一竖两个矩形。

T4：路径一定是 'Z' 型的，否则不优。设 $f_i$ 表示第一次到 $i$ 且前 $i - 1$ 个路灯都点燃的最早时间，那么有两种可能：

先从 $j$ 走到 $i - 1$，回到 $j$ 已经可以点燃，再走到 $i$：$f_i = f_j + 3(a_{i - 1} - a_j) + a_i - a_{i - 1},\quad 2(a_{i - 1} - a_j) \ge t$。
先从 $j$ 走到 $i - 1$，回到 $j$ 还不能点燃，等待至 $t$ 秒，再走到 $i$：$f_i = f_j + t + a_i - a_j,\quad 2(a_{i - 1} - a_j) < t$。

第一种情况即求 $2(a_{i - 1} - a_j) \ge t$ 的最小 $f_j - 3a_j$，开一个指针维护 $j$ 的边界。第二种情况 $2a_j + t > 2a_{i - 1}$，单调队列维护。

6/5

CF1873F *1300

每次钦定 $r$，维护 $l$ 最小值，发现 $l$ 只增不减，时间复杂度 $O(n)$。

CF985C *1500

首先排序。$a_1$ 一定是 $v_1$，所有合法 $v_i$ 满足 $v_i - v_{i - 1} \le k \land v_i - v_1 \le l$，且如果 $a_i, \ a_j$ 对应一组 $v_i, v_{i + 1}$，则 $\forall k \in (i, j)$，$a_k$ 也可以插入 $v$。

那么可以先确定间隔最长且合法的点，如果不满 $n$ 个，再从高到低插入中间的数。

CF898D *1600

按时间排序，枚举区间右端点 $r$，维护最小的 $l$ 满足 $t_r - t_l < m$，如果这个区间闹钟数大于 $k$，对后续区间而言，把 $r$ 删掉一定是最优的。

CF862C *1900

对于 $n = 1$ 或 $2$，直接特判掉。如果 $n = 2, x = 0$，无解。

第一个想法，随机 $n - 1$ 个不同的数，那么第 $n$ 个数已经确定，但有较大概率与之前重复，当然可以多随机几遍，这样做是不优的。

只随机前 $n - 2$ 个数，满足每个数小于 $2^{17}$，随机 $a_{n - 1} > 2^{17}$，由于 $x < 2^{17}$，$a_n$ 一定大于 $2^{17}$，不与前 $n - 2$ 个数重复，唯一非法情况是 $a_{n - 1} = a_n$，显然概率很低，多随机几遍。

不要随机，是否有确定算法？指定 $i \in [1, n - 3],\ a_i = i,\ a_i < 2^{17}$，指定 $a_{n - 2} = 2^{17}$，则 $r = \bigoplus_{i = 1}^{n - 2}a_i \in [2^{17}, 2^{18})$，指定 $a_{n - 1} = 2^{18}$，则 $a_{n} = x \oplus r\oplus a_{n - 1} > 2^{18}$。（$17, 18$ 位都是 $1$）。

CF1579E2 *1700

对于一个数而言，前一个数加在左边还是右边的影响都是一样的，所以只需考虑当前最优决策。

CF1949I *1800

在相切的圆间连边。对于点 $i$，如果 $r_i$ 减 $x$，那么与 $i$ 直接相连的 $r_j$ 必须加 $x$，我们可以由一个点的变化情况推出整个连通块的变化情况。

类比成染色问题。如果一个连通块存在奇环，则半径不能够改变。否则可以染成黑白两色，如果黑点数不等于白点数，说明半径可以减小。

CF1209G1 *2000

由于操作是把所有 $x$ 都变成 $y$，因此只要两个区间（一个数第一次和最后一次出现的位置）有交集，就必须合并。一个区间会变成其所在连通块里出现次数最大的元素。现在只要合并每个区间，将所有区间按左端点排序，从前往后遍历，不断更新当前连通块左右边界。

CF1133F2 *1900

如果 $\deg(1) < D$，无解。把 $1$ 删除，图分为若干联通块，$1$ 至少向每个联通块连一条边，所以如果连通块数大于 $D$，无解。

否则 $1$ 先向每个连通块连一条边，再在剩余儿子里凑满 $D$ 条出边。对于其他节点，遍历每一条边，并查集维护生成树性质（类似 kruscal）。

CF985G *2700

简单容斥，$\text{答案}=\text{全集} - \begin{matrix}(i, j)\text{ 有边}\\(i, k)\text{ 有边}\\(j, k)\text{ 有边}\end{matrix} + \begin{matrix}(i, j)(i, k)\\(i, j)(j, k)\\(i, k)(j, k)\end{matrix} - (i, j, k)\text{ 是三元环}$。

前三项直接算贡献，最后一项利用无向图三元环的 trick，度数大的向度数小的连有向边，复杂度 $O(N\sqrt N)$（$n, m$ 同阶）。

5/31

CF1796D *2000

法一：$O(nk)$

设 $f_{i, j}$ 表示以 $i$ 结尾，已经加了 $j$ 个位置的最大子段和，则 $f_{i, j} = \begin{cases}a_i - x + \max(f_{i - 1, j}, 0)\\a_i + x + \max(f_{i - 1, j - 1}, 0) \end{cases}$.

合法方案为所有 $f_{i, j}$ 满足 $i \le n - (k - j)$，因为没填的 $k - j$ 个位置可以在 $i$ 后面随便放。

法二：$O(n)$

如果 $x < 0$，令 $k \to n - k,\ \ x \to -x$。

子数组长度 $> k$，不妨将所有 $a_i$ 先减去 $x$，最后再加 $2kx$，设 $s_i = \sum_{j = 1}^i a_j - x$，则最大值为 $2kx + s_i - \min(s_j), \quad j < i - k$。
子数组长度 $\le k$，数组的每个位置都能加 $x$，设 $s_i = \sum_{j = 1}^i a_j + x$，则最大值为 $s_i - \min(s_j), \quad i - k\le j < i$，单调队列维护。

CF1671D *1600

两个相邻的数 $a, b$ 间插入任何数都不会使答案变小，但如果插入 $a \sim b$ 之间的数则不改变答案。

因此，只要先插入 $1$ 和 $x$，$2 \sim x$ 一定能插到某两个数中间而不使答案改变。

分别枚举 $1, x$ 插到同一个位置和不同位置的情况，复杂度 $O(n)$。

CF1217C *1700

整数 $x$ 的有效长度 $len(x) = \lfloor\log_2x\rfloor + 1$。

设 $[l, r]$ 对应的整数为 $x$，如果 $x = r - l + 1$，那么其有效长度一定是 $\log$ 级别的。

因此枚举每个 $s_i = 1$ 作为最高位，向后枚举至多 $len(n)$ 位。

设 $[i, j]$ 对应 $cur$，如果 $i$ 之前有至少 $cur - len(cur)$ 个 $0$，则将答案加一。

CF950D *2100

只有前 64 层对答案有用，暴力维护每层右移多少次，计 $add_d$ 为 $d$ 层右移次数。

操作一：$add_d \to (add_d + k) \bmod 2^d$。

操作二：$add_d \to (add_d + k) \bmod 2^d, \ \ add_{d + 1} \to (add_{d + 1} + 2k) \bmod 2^{d + 1}\cdots$。

操作三：对与一个值 $x$，与其现位置 $p$ 有关系 $\begin{cases}p = 2^d + (x + add_d) \bmod 2^d \\x = 2^d + (p - add_d) \bmod 2^d \end{cases}$，其中 $d - 1$ 层的位置 $p_{d - 1} = p_d \operatorname{>>} 1$。

5/29

P7077 [CSP-S2020] 函数调用 *提高+/省选−

将函数与其调用的函数间连边（非相邻操作间连边），建一个虚拟函数 0 向所有 q 个操作连边，题目保证这是一张 DAG.

一个加操作 add(p, v) 等效于给 p 加上 v 乘上后面所有乘操作的系数，转化为求每个加操作会被实际执行多少次（倍）。

定义 mul(x) = Π mul(son) 为执行 x 会使在 x 之前的操作扩大多少倍。

于是可以按拓扑序递推每个函数的执行次数，cnt(x) = Σ cnt(fa) × (相同父节点的在 x 右侧的节点 mul 之积)，初始化 cnt(0) = 1.

CF1843E *1600

答案有单调性，二分。如果和我一样没脑子可以写主席树 mlogn check，但是为什么不 O(n) 重构 O(n) 维护前缀和呢？

CF1148C *1700

从前往后枚举，保证 1 ~ i - 1 已经有序，如果 i != ai，设 i 原来位置为 t，显然有 t > i

如果 t - i >= n / 2，swap(i, pi)

再如果 t <= n / 2，swap(t, n) --> swap(i, n)

再如果 i > n / 2，swap(1, t) --> swap(1, i) --> swap(1, t)

否则 i <= n / 2，swap(1, t) --> swap(1, n) --> swap(1, t) --> swap(i, n)

CF609D *2000

二分天数，把物件按价格排序，枚举第一类物品有多少件即可。

P7516 [省选联考 2021 A/B 卷] 图函数 *省选/NOI−

设 g(x, i) 表示枚举到 x 时是否有 x --> i 且 i --> x。当 x = i 时，g(x, i) = 1，当 x > i 时，i 自己都被删掉了，显然没有贡献。

g(x, i) 等效于问 x --> i 和 i --> x 是否各存在一条不经过 [1, x) 的路径。

（证明：如果 y < x 被删掉，一定不能经过，否则 y --> i 和 i --> y 一定有一边不连通，也能推出矛盾。）

所求的 h(G) 转化为 G 中满足 g(y, x)，y < x 的二元组数量。

要满足 x,y 路径间的中转点 >= y，很容易想到 floyd 倒序枚举中转点。

从后往前加边，将 g(y, x) 统计进满足 g(y, x) = 1的 i 最大的 h(Gi)，最后做一遍后缀和。特殊的，当边集为空时 h(G_m + 1) = n，即所有 g(x, x)。

5/19
int ans[0]

5/13
全新模数：1e7 + 9
字典树写的t[x].s[ch - '0']

5/5
首黑！（水黑？

5/4
取模取错调两个小时 😃

5/3
数论 master
距离上一次对矩阵乘法用费马小定理已经是两个月前的事了

4/27
再auto下去有生之年能用上py++（

4/14
笑点解析：卡A

4/10
全排列是 2^n 的（

4/5
不懂hack数据卡long long的意义，显得你小学数学很好吗
不给数据的oj都该被消灭！

4/4
笑点解析：数组少开1b调一个小时

4/2
十行的贪心写了一百行ds，鉴定为贪心的神

4/1
忘了lower_bound能加范围，所以用平衡树，鉴定为学whk学的

3/21
很喜欢1+2场, 可以探究掉分的极限

3/16
不喜欢abc，因为出爆搜题不会写 😃

3/14
感谢作弊老哥，使我的rating +5

3/12
红题调40分钟，原因是atcoder老题目判换行 😃

3/10
一个月没写主席树写出了惊为天人的东西

3/9
指令集怎么越开越慢啊
5s的时限都无法拯救带修莫队+stl 玩家

3/3
做英语阅读有种选这个选项会进哪条线的美感（
新版c++函数不写返回值直接起飞

3/2
线段树忘开4倍和别人求助，望周知
我为什么要压行。
t[x] = pushup(build(rs, mid + 1, r), build(ls, l, mid)); 是先做右边再做左边

3/1
若智题最后5s改完没交上去

2/25
两个log你开 0.3s/10MB ??

2/18
shaber 贪心用爆搜，div3的不是比赛而是我 🤡

2/17
BC 两道构造，😃
怎么一篇看的下去的题解都没有，你dp不写状态含义几个意思啊

2/16
谁让你把编号翻译成个数的？
div2 rating change = 0，但是 specialist

2/14
你div3天生克我是吧

2/10
省流：+2

2/8
byd 矩阵乘法用费马小定理

2/7
经鉴定，构造能力为0，重回1400，开心（

2/3
怎么力扣开定长vector就T，不开就过
好，D是爆搜 🤡
经典不会D，开摆
abc怎么G放树套树的板子啊，还是超级削弱版
split + merge >> rotate + splay

2/2

__builtin_popcountll 也能 long long
__builtin_popcount 只能处理 int，long long 要 __popcount，但要 c++20

2/1

我的水平：蓝色的ds 绿色的dp 红色的贪心（
小粉兔半夜直播打原神（

1/30

都 2024 年了怎么还有用 iterator 遍历容器的
wrong answer On line 3382 column 2, read 7, expected 6.

1/29

usaco silver >> Lu_xZ

1/28

本着不拿耻辱暴力分的原则，以0分高分斩下洛谷rk800 😃
洛谷怎么也出智慧数数题，神tm 普及/提高-
难绷, B Time limit exceeded on test 24，掉大分
赛后5分钟出E,挺板的线段树,一个极其智障的地方调半天，继续 specialist 😃

1/23

3h for 自己数据生成器写炸 🤡
P5356 [Ynoi2017] 由乃打扑克 hack 数据毁我青春

1/21

喜欢坐牢就去打arc(不提交为什么会掉分啊

1/19

A做40分钟，赛后3分钟出D，最大小丑

1/10

1h for while(l > L) update(seq[++ l], res);

1/8

用 cin 读 int，如果输入一个 long long ，后续读入都会有问题

1/7

判割点用 low[y] <= low[x] (应为 low[y] <= dfn[x])

1/6

一个 void 的函数写成 int
本地跑非常对，评测机疯狂 RE
st 表用 logl(r - l + 1)
调黄题调半个小时

posted @ 2024-05-29 09:44 Lu_xZ 阅读(81) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 20241021-1031杂题记录

· 训练记录（Jul.）

· 2 月做题记录

· 2024.1 做题记录

· The 2023 ICPC Asia Jinan Regional Contest / The 2nd Universal Cup. Stage 17: Jinan

阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 单线程的Redis速度为什么快？
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决：字节Trae VS Cursor，谁才是开发者新宠？
· 展开说说关于C#中ORM框架的用法！

公告

昵称： Lu_xZ
园龄： 1年5个月
粉丝： 6
关注： 10

+加关注

2025年3月

日

一

二

三

四

五

六

Lu_xZ

训练记录（Jun.）

公告

搜索

常用链接

我的标签

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论