20231112多校模拟T2
题目描述
给你下列7种形状，问恰好填满 \(n*2\) 的方格有多少种方案（每种形状可任意旋转）
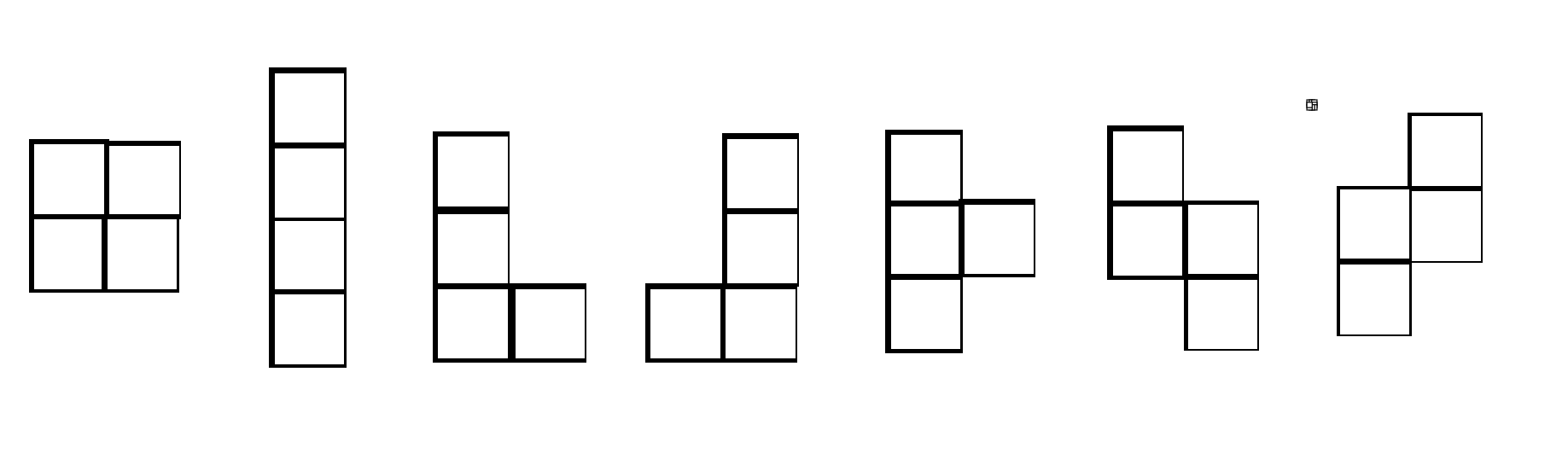
后三种形状纯粹是出题人的恶趣味，
d用没有
做法一：暴力
不会
做法二：递推
定义：
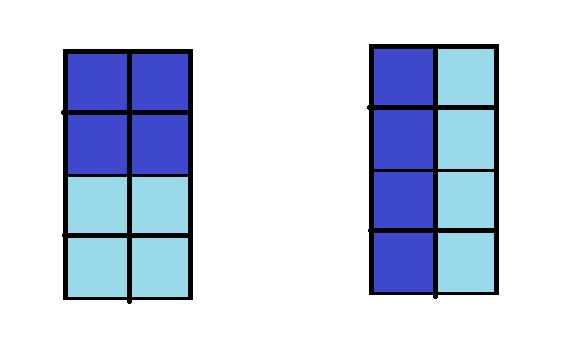
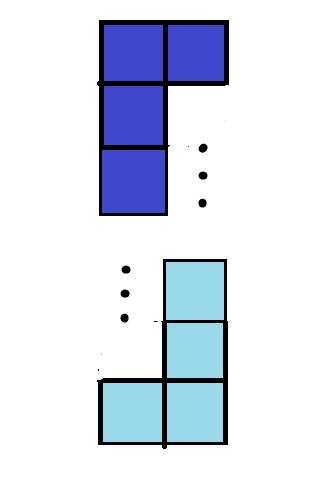
- f[i] 为填满 \(i*2\) 的方格的方案数
- g[i] 为填满 \(i*2\) 的方格 不能被腰斩 的方案数
解释：例如当 \(n = 4\) 时，下列第一种画法能被腰斩，第二种不能
初步分析
很容易得到, 当 \(i\) 为奇数时 答案答案显然为0
且
\[f[0] = 1, g[0] = 1, f[2] = 1, g[2] = 1, f[4] = 4, g[4] = 3
\]
当i为大于4的偶数时
\[f[i] = g[i] * f[0] + g[i - 2] * f[2] + g[i - 4] * f[4] + ... + g[2] * f[i - 2]
\]
进一步发现
\[g[i] = 2
\]
解释：上下两端用第3， 第4种方块， 中间用2填满
然后可以得到递推式
\[f[i] = 2 * (f[0] + f[2] + f[4] + ... f[i - 6]) + 3 * f[i - 4] + f[i - 2]
\]
前面一部分可用前缀和优化一下变为：
\[f[i] = 2 * (sum[i - 6]) + 3 * f[i - 4] + f[i - 2]
\]
发现奇数项根本没有用，优化一下空间
\[f[i] = 2 * (sum[i - 3]) + 3 * f[i - 2] + f[i - 1]
\]
此时答案为 \(f[\dfrac{n}{2}]\)
进一步优化
\(O(n)\) 做法跑 \(10^{18}\) 肯定会爆，考虑上述式子用矩阵乘法优化
\[\left[ \begin{matrix}
f[i] \\
f[i - 1] \\
sum[i - 2]
\end{matrix}
\right] =
\left[
\begin{matrix}
1 & 3 & 2\\
1 & 0 & 0\\
0 & 1 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
f[i - 1] \\
f[i - 2] \\
sum[i - 3]
\end{matrix}
\right]
\]
至此，复杂度优化为\(O(logn)\)
AC代码
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const ll P = 1e9 + 7, N = 2e6;
ll f[3] = {1, 1, 4};
ll sum[3] = {1, 2, 6};
ll n;
void mul(ll a[3][3], ll b[3][3]) {
ll c[3][3]; memset(c, 0, sizeof c);
for(int k = 0; k < 3; k ++) {
for(int i = 0; i < 3; ++ i)
for(int j = 0; j < 3; ++ j)
c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % P;
}
memcpy(a, c, sizeof c);
}
ll q_pow(ll b) {
if(b < 3) return f[b];
ll ret[3][3] = {1, 0, 0, 0, 1, 0, 0, 0, 1};
ll a[3][3] = { 1, 3, 2, 1, 0, 0, 0, 1, 1};
++ b;
while(b) {
if(b & 1) mul(ret, a);
mul(a, a);
b >>= 1;
}
return ret[1][0];
}
int main() {
while(scanf("%lld", &n) != EOF) {
if(n & 1) puts("0");
else printf("%lld\n", q_pow(n / 2));
}
return 0;
}
其他做法
机房大佬说这题就是斐波那契第n项的平方
我太弱了不会推
