深度学习之正则化方法

神经网络的拟合能力非常强，通过不断迭代，在训练数据上的误差率往往可以降到非常低，从而导致过拟合（从偏差-方差的角度来看，就是高方差）。因此必须运用正则化方法来提高模型的泛化能力，避免过拟合。

在传统机器学习算法中，主要通过限制模型的复杂度来提高泛化能力，比如在损失函数中加入L₁范数或者L₂范数。这一招在神经网络算法中也会运用到，但是在深层神经网络中，特别是模型参数的数量远大于训练数据的数量的情况下，L₁和L₂正则化的效果往往不如在浅层机器学习模型中显著。

于是，在训练深层神经网络时，还需要用到其他正则化方法，比如dropout、早停、数据增强和标签平滑等。

一、L₁和L₂正则化

L₁和L₂正则化在神经网络中的运用和其他机器学习方法一样，通过约束权重的L₁范数或者L₂范数，对模型的复杂度进行惩罚，来减小模型在训练数据集上的过拟合问题。

在损失函数中加入L₁和L₂正则化项，则结构风险最小化问题可以写为：

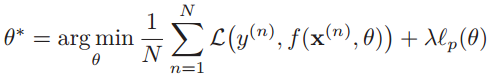
N为训练样本数量，f(•)为待学习的神经网络模型，θ是权重，l_p(θ)表示范数函数，p∈{0,1}，λ是正则化参数。

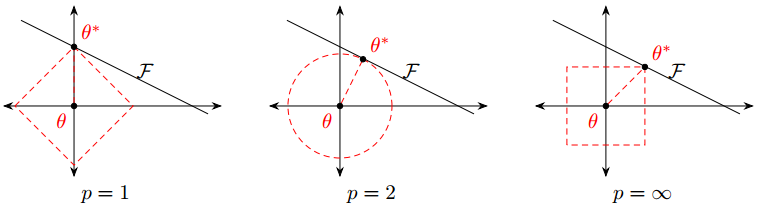
这里有三个问题：

1、为什么只正则化权重θ（通常用W表示），而不正则化偏置b呢？

其实也可以正则化偏置值，但是对于某一隐含层上的神经元来说，权重θ是一个高维的参数矩阵，已经可以表达高方差问题，而偏置b仅仅是单个数字，对模型的复杂度影响不大，因此一般选择忽略不计。

2、选择L₁正则化还是L₂正则化呢？

答案是一般选择L₂正则化，或者同时加入L₁正则化和L₂正则化。从上图可以看到，L₁正则化通常会使得最优解在y坐标轴上，从而使得最终的参数θ是稀疏向量，也就是说θ中很多值为0。此外，L₁范数在取得最小值处是不可导的，这会给后续的求梯度带来麻烦。

3、神经网络中的L₂正则化有什么特殊之处呢？

在神经网络中，加入的L₂范数一般用Frobenius范数：

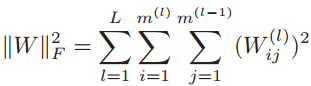
注意在Logistic回归中，参数W是一个向量，而在神经网络中，参数W是一个矩阵！上式中l表示第l层，m^(l)表示第l层的神经元个数，因此W是一个m^(l)  × m^(l-1)维的多维矩阵。于是神经网络中的L₂范数是矩阵中所有元素的平方和，称为Frobenius范数。

此时结构风险函数为：

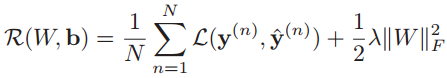
而且L₂正则化在神经网络中等价于通过权重衰减的方式来实现正则化。原因是，在损失函数中加入L₂正则化，然后用反向传播算法进行梯度下降更新参数时，会得到如下的形式：

也就是权重θ_t-1会乘以一个比1小的数，也就实现了权重衰减。

二、dropout

在深层神经网络的学习过程中，通过随机丢弃一部分神经元（同时丢弃其对应的连接边）来避免过拟合的做法，称为dropout（丢弃法，李宏毅老师称之为抓爆）。

dropout一般是在神经网络的隐含层中使用，实现dropout的方式可以是设置一个固定的概率p，对于每一个神经元都以一个概率p来判断要不要保留。同时，dropout在训练阶段和测试阶段的做法不一样。

1、训练阶段和测试阶段的dropout

我们通过定义一个公式来描述训练阶段和测试阶段的dropout实现过程，以及二者之间的区别。

对于一个神经网络层y=f(Wx+b)，引入一个丢弃函数d(•)，使得y=f(Wd(x)+b)。丢弃函数定义为：

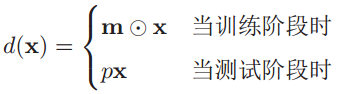
在训练阶段中，m∈{0,1}^d是丢弃掩码，通过概率为p的0-1分布（伯努利分布）来随机生成。p值一般设置为0.5就能产生比较好的效果，复杂点也可以通过验证集来选取一个最优值，那么训练时激活神经元的平均数量是原来的p倍。举个例子就是神经元有5个，p=0.6，然后随机生成m=[1, 0, 1, 1, 0]，于是训练过程中这一层中的第2和第5个神经元就会被丢弃，也就是神经元的数量变成了原理的0.6倍。

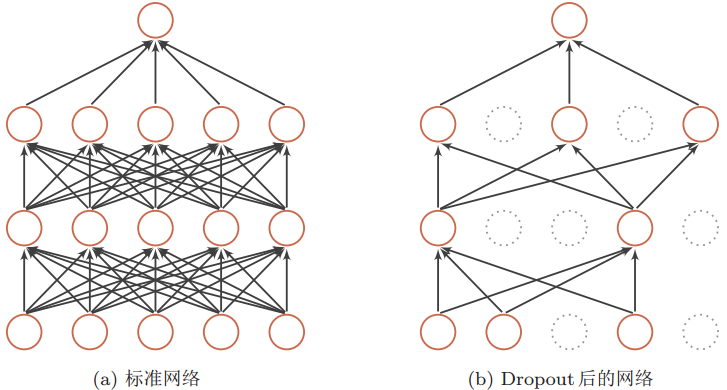
部分隐含层神经元被丢弃的结果就是，在反向传播时，和被丢弃神经元相关的权重的梯度为0。而在训练中每个隐含层神经元都有可能被以p的概率丢弃，这样就减少了神经元之间的依赖性，输出层的计算也无法过度依赖任何一个隐含层神经元，从而减少过拟合。

而在测试阶段，为了得到更确定的结果，一般不丢弃神经元。所有神经元都可以激活，这会造成训练和测试时的网络输出不一致，因此在测试时将每一个神经元的输出都乘以概率p，相当于把不同的神经网络做平均，从而在网络输出上和训练阶段保持一致。

以下是一个神经网络使用dropout后的图示：

2、为什么dropout的效果特别好？

dropout不仅能减少过拟合，而且能提高预测的准确性，这可以从集成学习的角度来解释。在迭代过程中，每做一次丢弃，就相当于从原始网络中采样一个不同的子网络，并进行训练。那么通过dropout，相当于在结构多样性的多个神经网络模型上进行训练，最终的神经网络可以看做是不同结构的神经网络的集成模型。

3、循环神经网络中的dropout的特殊性

在循环神经网络上使用dropout时，不能直接对每个时刻的隐状态进行随机丢弃，这样会损害循环神经网络在时间上的记忆能力，而是应该在非时间维度的连接上进行随机丢弃。

如下图，虚线的前馈连接表示非时间循环的连接，而实线的连接表示时间维度上的循环，即隐状态（粗实线表示典型的LSTM中的信息流路径）。如果dropout设置在隐状态上，也就是从左往右的实线位置上，那么每经过一次循环，剩下的信息就会被丢弃一次，如果是长序列，那么循环到最后信息会丢失殆尽。

而把dropout设置在非时间循环的连接上，也就是从下到上的虚线位置，那么对信息进行丢弃就不会影响到对信息的记忆能力。

三、数据增强

减少过拟合的一种思路是增加训练集中的样本数量，尤其在训练深层神经网络的过程中，需要大量的训练数据才能得到比较理想的结果。但是增加样本是需要花费较多资源去搜集和标注更多的样本，因此可以基于现有的有限样本，可以通过数据增强（Data Augmentation）来增强数据，避免过拟合。

目前数据增强主要应用在图像数据上，在文本等其他类型的数据上还没有比较好的应用。

图形数据的增强主要是通过对图像进行转变、引入噪声等方法来增加数据的多样性，生成的假训练数据虽然无法包含像全新数据那么多的信息，但是代价几乎为零。增强的方法有：

（1）旋转：将图像按顺时针或者逆时针方向随机旋转一定角度；

（2）翻转：将图像沿水平或垂直方向随机翻转一定角度；

（3）缩放：将图像沿水平或垂直方向平移一定步长；

（4）加噪声：加入随机噪声。

四、早停

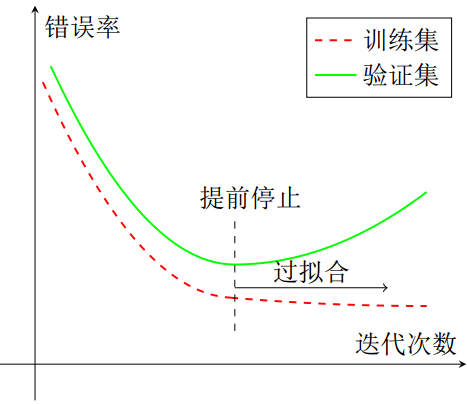
早停（early stopping）就是在训练误差下降到一定程度之前，提早停止神经网络的训练。那么在观察到什么信号时停止呢？答案是迭代了多轮之后，验证集上的错误率仍然没有下降时，就停止迭代。

也就是说，在使用梯度下降法进行优化时，可以使用一个和训练集独立的样本集合，称为验证集，在每次迭代时，把新学习到的模型f(x, θ)在验证集上进行测试，并计算错误率，用验证集上的错误来代替期望错误。验证集上的误差率通常会先下降后上升，而在拐点处就预示着开始过拟合了。

当验证集的错误率在经过多轮迭代后不再下降时（甚至还升高），就停止迭代。因此在使用早停来解决过拟合时，训练和验证要同时进行，或者交叉进行。

五、标签平滑

在数据增强中，是通过给样本特征加入随机噪声来避免过拟合的，而标签平滑是通过给样本的标签（输出）引入噪声来避免过拟合。

假设训练数据集中，有些样本的标签是被错误标注的，那么最小化这些样本上的损失函数会导致权重往错误的方向去学习，从而导致过拟合。例如，在多分类问题中，一个样本的标签一般用one-hot向量表示，y=[0, ..., 0,1, 0, ...,0]^T，这种目标可以作为硬目标。如果使用softmax分类器并采用交叉熵损失函数，那么最小化损失函数会使得正确类和其他类之间的权重差异变得非常大。一方面使用softmax分类器和硬目标的最大似然学习可能永远不会收敛，因为softmax函数永远无法真正预测0概率或者1概率，而只能通过学习越来越大的权重，来不断趋近于0或1。另一方面要使得正确类的输出概率接近于1，那么未归一化之前的得分要远大于其他类的得分，这就得到其权重越来越大。权重越大，模型的复杂度越高，也就是产生过拟合问题。

因此使用硬目标来进行最大似然学习的问题在于，模型无法真正拟合到硬目标上，在不断逼近硬目标的过程中会过拟合。

标签平滑的做法是，假设样本为其他类的概率为ε，为正确类的概率为（1-ε），那么把标签表示为：

其中K为标签的数量，这种标签可以看做是软目标。标签平滑之后，模型不会追求确切的概率（0或者1），而且不影响模型学习正确分类。

 

参考资料:

1、邱锡鹏：《神经网络与深度学习》

2、《Deep Learning》（花书）

3、吴恩达：《深度学习》