Go排序算法小总结

Go-排序算法

参考整理：1.0 十大经典排序算法 | 菜鸟教程 (runoob.com)

shell排序 - Mohuishou (lailin.xyz)

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

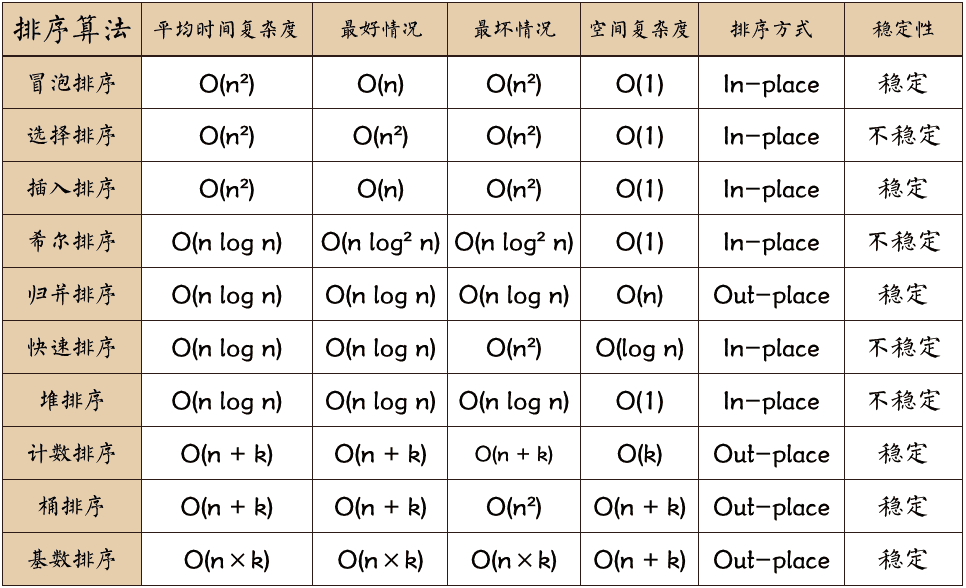
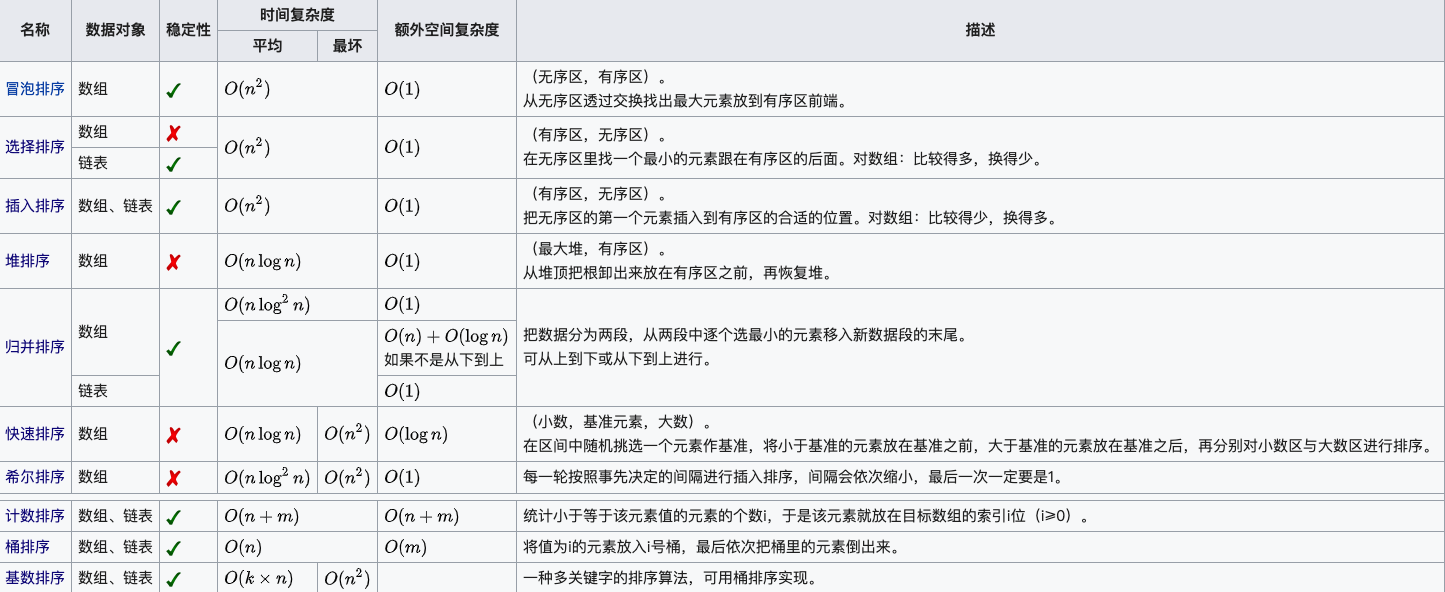
点击以下图片查看大图：

关于时间复杂度

平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序

线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序，计数、桶排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

• n：数据规模
• k："桶"的个数
• In-place：占用常数内存，不占用额外内存
• Out-place：占用额外内存
• 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

一下是部分排序的实现，先是不稳定的排序。

不稳定排序算法实现

1. 快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 Ο(n log n)次比较。在最坏状况下则需要 Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他 Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项之可能性。

步骤

• 从数列中挑出一个元素，称为 “基准”（pivot），
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

注意: 基准点采用三元素原则法，三元素选择之后一头一尾就已经有序了

实现

package quik
//Sort 快速排序
func Sort(arr []int) {
	Quik(arr, 0, len(arr)-1)
}
//Quik 快速排序递归实现
func Quik(arr []int, left int, right int) {
	if right-left < 2 {
		return
	}
	p := middle3(arr, left, right)
	i := left + 1
	j := right - 2
	for {
		for arr[i] < p {
			i++
		}
		for arr[j] > p {
			j--
		}
		if i < j {
			arr[i], arr[j] = arr[j], arr[i]
		} else {
			break
		}
	}
	arr[i], arr[right-1] = arr[right-1], arr[i]
	Quik(arr, left, i-1)
	Quik(arr, i+1, right)
}

func middle3(arr []int, left int, right int) int {
	center := (right + left) / 2
	if arr[left] > arr[center] {
		arr[left], arr[center] = arr[center], arr[left]
	}
	if arr[left] > arr[right] {
		arr[left], arr[right] = arr[right], arr[left]
	}
	if arr[center] > arr[right] {
		arr[center], arr[right] = arr[right], arr[center]
	}
	arr[center], arr[right-1] = arr[right-1], arr[center]
	return arr[right-1]
}

2. 选择排序

选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾。以此类推，直到所有元素均排序完毕。

示例

示例图片

实现

package selection
//Sort 选择排序
func Sort(arr []int) {
	var LEN = len(arr)
	minIndex := 0
	for i := 0; i < LEN; i++ {
		minIndex = i
		for j := i; j < LEN; j++ {
			if arr[minIndex] > arr[j] {
				minIndex = j
			}
		}
		if minIndex != i {
			arr[minIndex], arr[i] = arr[i], arr[minIndex]
		}
	}
}

3. 希尔shell排序

希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

步骤

1. 设置间隔（传统间隔为 N/2）
2. 插入排序

程序示例

传统实现

//SortInt 传统shell排序,间隔为N/2
//相邻间隔可能不互质，可能会出现前置排序无用的情况
func SortInt(a []int) ([]int, int) {
	n := 0
	aLen := len(a)
	//定义间隔
	for i := aLen / 2; i > 0; i = i / 2 {
		//插入排序
		for j := i; j < aLen; j++ {
			tmp := a[j]
			k := j
			for ; k >= i && tmp < a[k-i]; k = k - i {
				a[k] = a[k-i]
				n++
			}
			a[k] = tmp
		}
	}
	return a, n
}

Hibbard 算法

//SortHibbardInt Hibbard算法，间隔为2^k-1
func SortHibbardInt(a []int) ([]int, int) {
	n, i := 0, 0
	aLen := len(a)
	for i = 1; i <= aLen-1; i = i*2 + 1 {
	}
	//定义间隔
	for ; i > 0; i = (i - 1) / 2 {
		// println(i)
		//插入排序
		for j := i; j < aLen; j++ {
			tmp := a[j]
			k := j
			for ; k >= i && tmp < a[k-i]; k = k - i {
				a[k] = a[k-i]
				n++
			}
			a[k] = tmp
		}
	}
	return a, n
}

4. 堆排序

堆积排序： 是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

步骤

• 建堆，建堆是不断调整堆的过程，从 len/2 处开始调整，一直到第一个节点，此处 len 是堆中元素的个数。建堆的过程是线性的过程，从 len/2 到 0 处一直调用调整堆的过程，相当于 o(h1)+o(h2)…+o(hlen/2) 其中 h 表示节点的深度，len/2 表示节点的个数，这是一个求和的过程，结果是线性的 O(n)。
• 调整堆：调整堆在构建堆的过程中会用到，而且在堆排序过程中也会用到。利用的思想是比较节点 i 和它的孩子节点 left(i),right(i)，选出三者最大(或者最小)者，如果最大（小）值不是节点 i 而是它的一个孩子节点，那边交互节点 i 和该节点，然后再调用调整堆过程，这是一个递归的过程。调整堆的过程时间复杂度与堆的深度有关系，是 lgn 的操作，因为是沿着深度方向进行调整的。
• 堆排序：堆排序是利用上面的两个过程来进行的。首先是根据元素构建堆。然后将堆的根节点取出(一般是与最后一个节点进行交换)，将前面 len-1 个节点继续进行堆调整的过程，然后再将根节点取出，这样一直到所有节点都取出。堆排序过程的时间复杂度是 O(nlgn)。因为建堆的时间复杂度是 O(n)（调用一次）；调整堆的时间复杂度是 lgn，调用了 n-1 次，所以堆排序的时间复杂度是 O(nlgn)[2]

注意: 根节点在数组当中存放的位置是 0，所以第 i 个节点的左孩子是 2i+1,右孩子是 2i+2

实现

package HeapSort
import (
	"fmt"
)
//HeapSort 堆排序
func HeapSort(arr []int) {
	LEN := len(arr)
	for i := LEN/2 - 1; i >= 0; i-- {
		HeapAjust(arr, i, LEN)
	}
	for i := LEN - 1; i > 0; i-- {
		arr[i], arr[0] = arr[0], arr[i]
		HeapAjust(arr, 0, i)
	}
}
//HeapAjust 堆调整
func HeapAjust(arr []int, start int, length int) {
	tmp := arr[start]
	for i := 2*start + 1; i < length; i = i * 2 {
		if i+1 < length && arr[i] < arr[i+1] {
			i++
		}
		if tmp > arr[i] {
			break
		}
		arr[start] = arr[i]
		start = i
	}
	arr[start] = tmp
}

稳定排序

5. 冒泡排序

冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

步骤：

1. 比较相邻的元素（从后往前）。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
   (如果这一步没有出现任何一次交换，那么说明所有的元素已经有序，不需要再进行下面的步骤了)
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

程序示例（go）

func SortInt(a []int) ([]int, int) {
	//交换次数，计数
	n := 0

	aLen := len(a)

	for i := aLen - 1; i >= 0; i-- {
		//标记，如果flag一次冒泡之后没有改变，那么证明排序已完成，不需要再次排序，直接退出
		flag := 0

		//一次冒泡
		for j := 0; j < i; j++ {
			if a[j] > a[j+1] {
				//交换两个变量的值，无需引入临时变量
				a[j], a[j+1] = a[j+1], a[j]

				n++

				//有交换，flag=1
				flag = 1
			}
		}

		//判断一次冒泡，是否存在交换
		if flag == 0 {
			break
		}

	}

	return a, n
}

6. 归并排序

归并排序:是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用

步骤

• 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
• 设定两个指针，最初位置分别为两个已经排序序列的起始位置
• 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
• 重复步骤 3 直到某一指针达到序列尾
• 将另一序列剩下的所有元素直接复制到合并序列尾

示例

package merge
//INFINITY 一个比较大的值用作哨兵
const INFINITY = 0xffff
func merge(arr []int, start, end int) {
	if start < end {
		//从中间划分，分别左右两边排序
		mid := (end + start) / 2
		merge(arr, start, mid)
		merge(arr, mid+1, end)
		//下面进行归并操作，将两个长度较小但是已经排序完成的数组合并成一个较长长度的排序数组
		//新建一个数组用于存放左边的值
		arr1 := make([]int, mid-start+2)
		copy(arr1, arr[start:mid+1])
		arr1[mid-start+1] = INFINITY
		//新建一个数组用于存放右边的值
		arr2 := make([]int, end-mid+1)
		copy(arr2, arr[mid+1:end+1])
		arr2[end-mid] = INFINITY
		//比较大小
		j, k := 0, 0
		for i := start; i <= end; i++ {
			if arr1[j] <= arr2[k] {
				arr[i] = arr1[j]
				j++
			} else {
				arr[i] = arr2[k]
				k++
			}
		}

	}
}

7. 插入排序

插入排序的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

步骤

1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置后
6. 重复步骤 2~5

程序示例（go）

//SortInt 插入排序
func SortInt(a []int) ([]int, int) {
	n := 0
	aLen := len(a)

	//从i=1开始，第一个数不用排序，一个数相当于已经有序了
	for i := 1; i < aLen; i++ {
		//取出新数（类似摸牌）
		tmp := a[i]

		//将新数和之前的数从后往前（从大到小）一次比较，如果新数更小,就将以前的数往后移一位
		j := i
		for ; (j > 0) && (tmp < a[j-1]); j-- {
			n++
			a[j] = a[j-1] //后移一位
		}
		//新数插入
		a[j] = tmp

	}
	return a, n
}