模式识别与机器学习（第四章学习记录和心得）

目录

• 思维导图
• 学习模型
  • • 一、判别模型
      • 1.1 线性判据
        • 1.1.1 简介
        • 1.1.2 感知机算法
        • 1.1.3 Fisher判据
        • 1.1.4 SVM
        • 1.1.5 多类分类
      • 1.2 线性回归
        • 1.2.1 关注点
        • 1.2.2 模型表达
        • 1.2.3 目标函数
        • 1.2.4 目标优化
      • 1.3 逻辑回归
        • 1.3.1 思想
        • 1.3.2 Logit变换
        • 1.3.3 Sigmoid函数
        • 1.3.4 逻辑回归
      • 1.4 Softmax判据
        • 1.4.1 思想
        • 1.4.2 Softmax函数
        • 1.4.3 Softmax判据
        • 1.4.4 适用范围
        • 1.4.5 总结
    • 二、生成模型

思维导图

学习模型

一、判别模型

1.1 线性判据

1.1.1 简介

1. 学习过程

   监督式学习

2. 识别过程

   将待识别样本代入训练好的判据方程

3. 目标函数（也可加入正则项提高泛化能力）
   

4. 目标函数的求解

   (1) 最小化/最大化目标函数

   (2) 解析求解（求偏导）/迭代求解（梯度下降法）

   (3) 约束条件

5. 梯度下降法

   (1) 更新方向：负梯度方向

   (2) 更新大小：步长×梯度幅值

1.1.2 感知机算法

1. 并行感知计算法

   (1) 并行：一次性给出所有训练样本用于训练

   (2) 目标函数：所有被错误分类的训练样本的输出值取反求和
   

   (3) 步骤

        /*
        预处理：增广向量+规范化
        初始化参数
        使用梯度下降法迭代更新参数
        根据停止条件（无错分或阈值等）来停止迭代
        */

2. 串行感知机算法

   (1) 串行：训练样本一个一个给出

   (2) 目标函数：对于当前被错误分类的训练样本，最小化其输出值取反
   

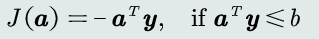
   (3) 步骤：类似并行感知机，不过每次迭代都串行地遍历每一个训练样本

3. 总结

• 收敛性：线性可分必收敛

• 解的最优性：

  1. 若目标函数满足L-Lipschitz条件，则可设定步长确保收敛到局部最优点；
  2. 若目标函数是凸函数，则局部极值就是全局极值

• 步长与收敛性：

  1. 步长越大，收敛越快，但可能会在极值点附近振荡；
  2. 步长越小，收敛速度越慢

• 算法改进：可通过加入Margin约束来提高算法的泛化能力（将正确分类的门槛提高，减少样本位于决策边界导致决策有很大不确定性的情况）

1.1.3 Fisher判据

1. 思想
   将原空间的点投影到新的一维空间（投影轴），找到一个最合适的投影轴，使两类样本在该轴上投影的重叠部分最少，从而达到最佳分类效果

2.目标函数

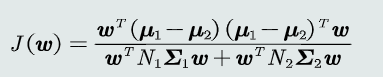
(1) 类间散度

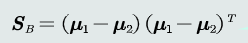
(2) 类内散度

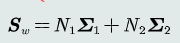
3. 判别函数
   

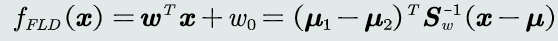
1.1.4 SVM

1. 思想

给定一组训练样本，使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大（支持向量即位于间隔边界上的样本，在确定决策边界中起到核心作用）

2. 带不等式约束的拉格朗日数乘法

(1) KKT条件

(2) 问题转化

在多个约束条件下最小化f(x)的问题可以转化为KKT条件下的拉格朗日函数优化问题

• 原问题
  

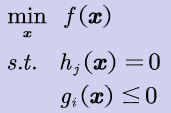
• 拉格朗日函数优化问题
  

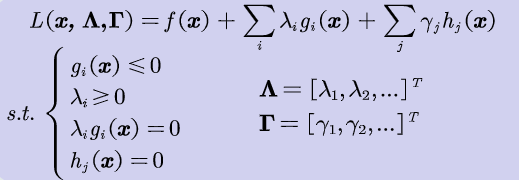
3. 主问题与对偶问题

(1) 主问题（难以求解）

(2) 对偶函数

(3) 对偶问题

(4) 主问题与对偶问题的关系

如果强对偶性成立，则能够保证对偶问题的最优值=主问题的最优值！

4. SVM学习算法

(1) 主问题目标函数

(2) 步骤

• 构建拉格朗日函数
  

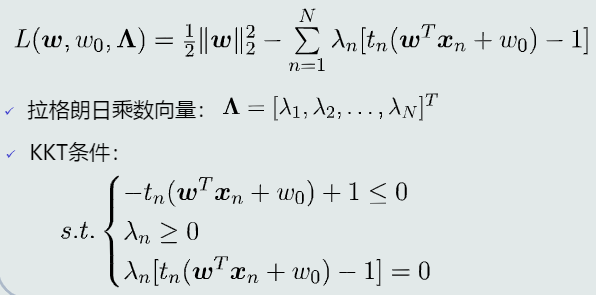
• 构建对偶函数并求解

  • SVM对偶函数
    

  • 解析法求解对偶问题
    

    

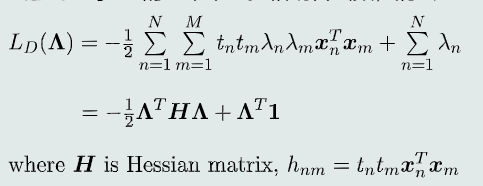
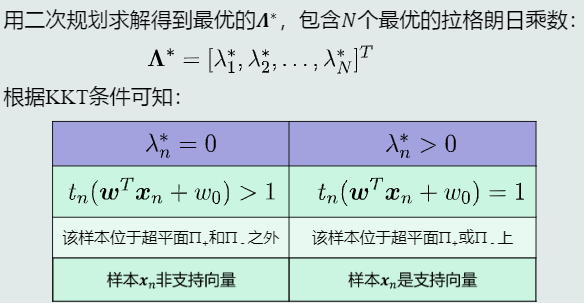
• 求解支持向量
  

• 求解参数最优解

  • 系数项
    

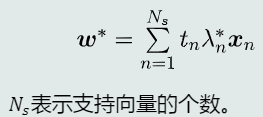
  • 偏置项（由所有支持向量取均值得到）
    

(3) 决策过程

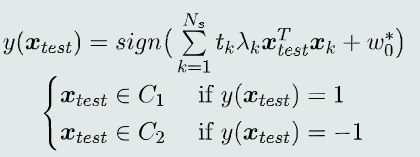
系数项和偏置的学习过程实际上是从训练样本中选择一组支持向量，并将这些支持向量存储下来，用作线性分类器

5. 软间隔SVM

(1) SVM的问题

有些训练样本带有噪声或是离群点，如果严格限制所有样本都在间隔区域之外，噪声点可能被选做支持向量，使得决策边界过于拟合噪声

(2) 思想

通过引入松弛变量，允许一些训练样本出现在间隔区域内形成软间隔。松弛变量可以将SVM的硬间隔放宽到软间隔，允许一些训练样本出现在间隔区域内，从而具备一定的克服过拟合的能力。

(3) 目标函数

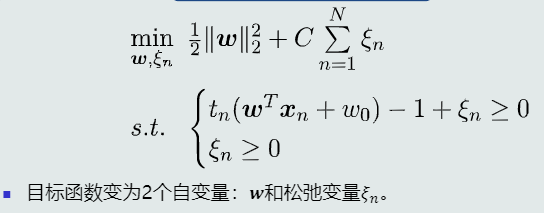
(4) 支持向量

• 支持向量的判断
  

• 两类支持向量
  

(5) 参数最优解

• 系数项
  

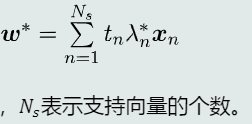
• 偏置项
  

6. 核SVM

(1) 思想

如果样本在原始特征空间线性不可分，可以将这些样本通过一个函数φ映射到一个高维的特征空间，使得在这个高维空间，样本更可能拥有一个线性分类边界

(2) 核技巧

现实中求取低维到高维的映射函数往往很困难，不过可以通过核函数求取两个高维空间的向量点积

• 核函数
  

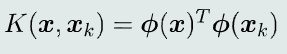
  • 核函数的条件：半正定对称函数

  • 常见的核函数

    a. 多项式核函数
    

    优点：
    
      1. 可以解决线性不可分问题
    
      2. 如果知道非线性分类边界的阶数，则可以直接定义m
    
    缺点：
    
      1. ρ值较大时，数值计算困难
    
      2. 超参数较多
    
    b. 高斯核函数
    

    

      优点：
    
        1. 比多项式核非线性程度更高
    
        2. 核函数输出值范围[0, 1]，数值计算难度不大
    
      缺点：
    
        1. 容易过拟合
    
        2. 比线性SVM速度慢很多
    

• 核SVM决策模型（x空间的决策边界是非线性的）
  

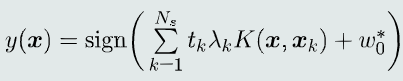
7. 软间隔核SVM

(1) 思想

核SVM（尤其是高斯核）很容易产生过拟合，所以通常会加入松弛正则项，即软间隔核SVM

(2) 对偶问题

1.1.5 多类分类

1. One-to-all

(1) 思想

• 假设每个类与剩余类线性可分

• 针对每个类，单独训练一个线性分类器

• 每个类对应的分类器用于识别样本是否属于该类

• 总共需要训练K个分类器（K为类别总数）

(2) 判别公式

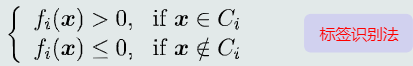
(3) 问题

• 每个分类器正负类样本个数不均衡

• 会有混淆区域：拒绝选项（针对单个测试样本x，所有分类器输出都不是正值），重叠（针对单个测试样本，会被多个分类器识别为正类）

2. 线性机

(1) 思想

基本思想与One-to-all差不多，不过决策条件改为了输出值投票法（max函数），选择输出值最大的那个类

(2) 判别公式

• 线性机 = K个线性模型 + 1个max函数
  

(3) 优势

使用max函数，不再有混淆区域（拒绝区域、重叠区域）（训练阶段）

(4) 问题

• 可能出现最大的输出值都是小于等于0的，此时测试样本出现在拒绝区域

• 如果严格按照线性判据的定义，拒绝区域其实是线性机（基于one-to-all策略）无法正确判断的区域

3. One-to-One

(1) 思想

• 假设任意两个类之间线性可分，但每个类与剩余类可能是线性不可分的

• 针对每两个类Ci和Cj，训练一个线性分类器，Ci类真值为正，Cj类真值为负

• 总共需要训练K(K-1)/2个分类器

(2) 判别公式

(3) 决策边界

Ci类与其他所有类的决策边界的正半边的交集

(4) 优势

• 避免了one-to-all策略正负样本个数不均衡的问题

• 适用于一些线性不可分的情况，从而实现非线性分类

• 与one-to-all策略相比，不再有重叠区域

(5) 问题

• 仍然会出现拒绝选项（拒绝区域）

• 改进：在决策过程中采用max函数来避免出现拒绝区域
  

4. 总结

• 使用线性判据进行多类分类，本质上是利用多个线性模型组合而成一个非线性分类器
• 决策边界不再是由单个超平面决定，而是由多个超平面组合共同切割特征空间

1.2 线性回归

1.2.1 关注点

输出值的具体数值（连续值）

1.2.2 模型表达

单个样本

1.2.3 目标函数

最小化均方误差

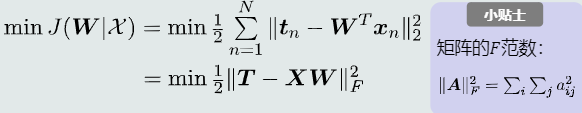
1.2.4 目标优化

1. 梯度下降法
   

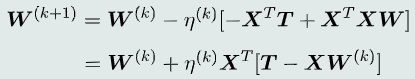
2. 最小二乘法
   

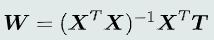
• 问题：使用最小二乘法要求X^T*X是可逆矩阵，当N >> P+1时（Tall数据）可能满秩，而当P+1 >> N时（Wide数据）不可能满秩，故最小二乘法适用于Tall数据
  （N为训练样本数，P为特征维数）

1.3 逻辑回归

1.3.1 思想

1. 对于二类分类，借鉴MAP分类器的做法，不过是通过比较两个后验概率的比例来做决策

2. 假设每类数据都是高斯分布且协方差矩阵相同，则x属于C1类的后验概率与x属于C2类的后验概率之间的对数比率就是线性模型f(x)的输出

1.3.2 Logit变换

1.3.3 Sigmoid函数

1. 表达式
   根据Logit变换可以反推出后验概率的表达式，将此表达式定义为Sigmoid函数
   

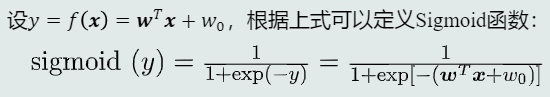
2. 意义
   Sigmoid函数是连接线性模型和后验概率的桥梁

   线性模型f(x) + Sigmoid函数 = 后验概率

1.3.4 逻辑回归

1. 定义

   线性模型f(x) + Sigmoid函数，输出值是属于C1类的后验概率
   

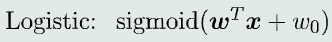
2. 决策过程

决策边界仍然是线性超平面

3. 适用范围

(1) 分类（前提是两类之间线性可分）

(2) 回归（可以拟合Sigmoid形式的非线性曲线）

4. 总结

(1) 逻辑回归本身是一个非线性模型

(2) 逻辑回归用于分类仍然只能处理两个类别线性可分的情况。但是Sigmoid函数输出了后验概率，使得逻辑回归成为一个非线性模型，因此，逻辑回归比线性模型向前迈进了一步

(3) 逻辑回归用于拟合只能拟合有限的非线性曲线

5. 学习过程

(1) 目标函数

最大似然估计法（假设对于输入样本，模型输出的类别标签服从伯努利分布）

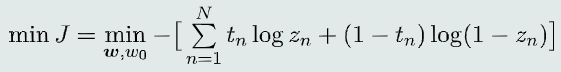
(2) 交叉熵

(3) 目标函数的优化

• 梯度下降法

  • 梯度消失问题

    迭代训练过程中，如果参数w选择较大的初始值，输出zn会很快进入Sigmoid饱和区，导致梯度接近于0，出现梯度消失现象。根据链式法则，目标函数关于参数的梯度也就接近于0，使得后续迭代更新不起作用，所以参数w应尽量选择较小的初始值。

• 迭代停止条件

  达到一定训练精度后提前停止迭代（若要求过高，则会出现过拟合问题）

1.4 Softmax判据

1.4.1 思想

改变基于后验概率的判别函数，使模型能够进行多类分类

1.4.2 Softmax函数

1. yi是线性模型的输出，zi是对应的后验概率P(Ci | x)
   

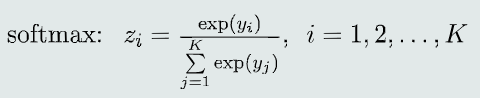
2. 特点：

• 若一个类对应的线性模型输出远远大于其他类，则
  该类的后验概率接近于1，其他类的后验概率接近于0，
  softmax决策就像是一个max函数

• softmax函数可微分

1.4.3 Softmax判据

1. 模型
   K个线性判据+Softmax函数

2. 决策过程
   给定测试样本x，根据Softmax判据确定其最大后验概率对应的类别
   

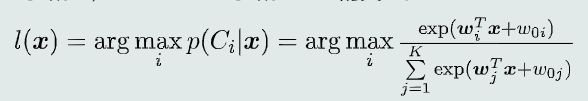
1.4.4 适用范围

1. 分类

(1) 前提是每个类和剩余类之间是线性可分的

(2) 等同于基于one-to-all策略的线性机

(3) 分类边界仍然是线性的

2. 回归
   可以拟合指数函数形式的非线性函数

1.4.5 总结

1. Softmax判据本身是一个非线性模型

2. Softmax判据用于分类只能处理多个类别、每个类别与剩余类线性可分的情况，但是，Softmax判据可以输出后验概率，比基于one-to-all策略的线性机向前迈进了一步

3. Softmax判据用于拟合，只能输出有限的
   非线性曲线

二、生成模型