模式识别与机器学习（第一至三章学习记录和心得）
基于距离的分类器源代码
python实现MED分类器
python实现MICD分类器
第一章 模式识别基本概念
1. 定义
2. 分类
3. 模式识别的数学解释
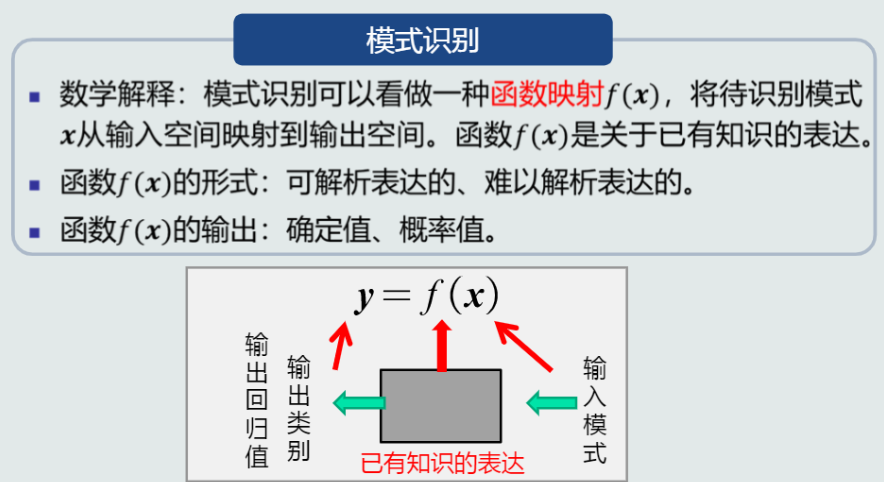
值得一提的是，机器学习的任务是学习上图中的函数\(f(\boldsymbol{x})\)
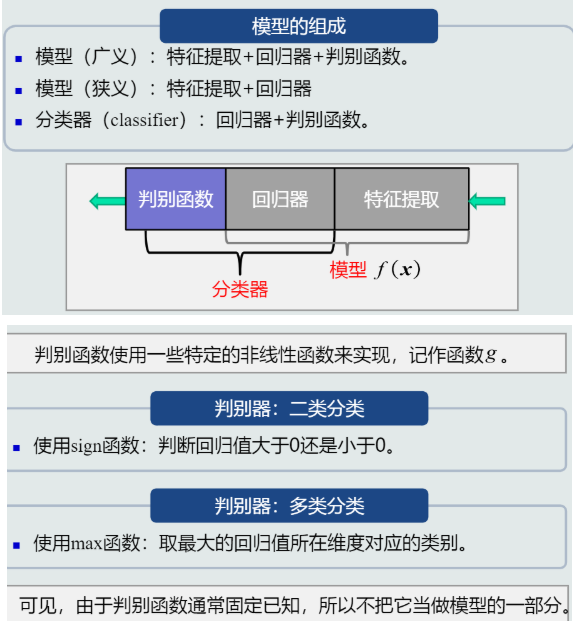
4. 模型
模型(model)：关于已有知识的一种表达方式，即函数\(f(\boldsymbol{x})\)。
- 用于回归的模型：
-
用于分类的模型：
与回归器相比，分类器只是在回归器末端加上了判别函数而已。
5. 特征
-
特征的特性：
(1) 具有辨别能力，提升不同类别之间的识别性能
(2) 鲁棒性，针对不同的观测条件（噪声、尺度变化等），仍能够有效表达类别
6. 特征向量
7. 特征向量的相关性度量
- 点积
- 投影
- 点积与投影的关系
- 残差向量
- 欧氏距离
8. 机器学习基本概念
- 训练样本：
-
模型的参数和结构：
-
线性模型：
-
非线性模型：
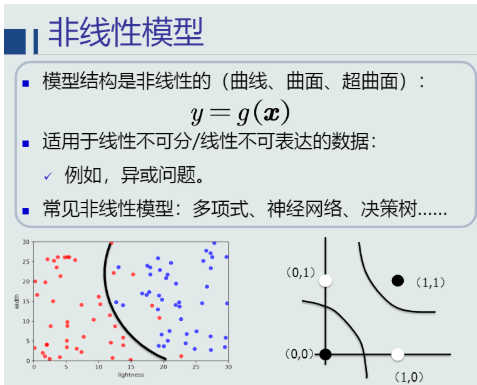
- 样本量与模型参数量的关系：
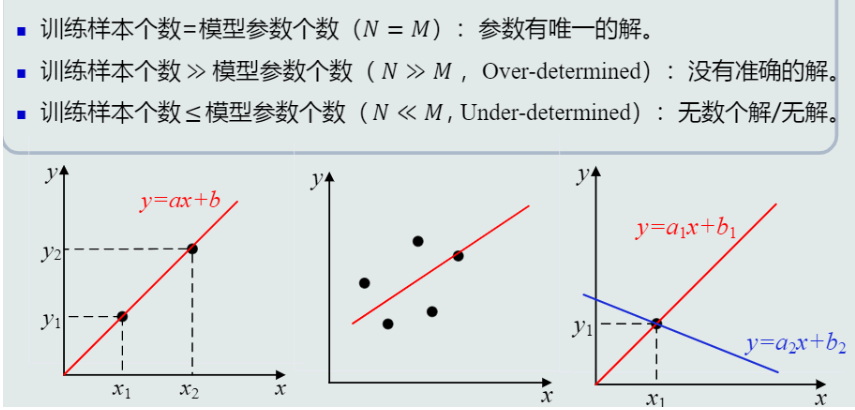
- 目标函数：
-
优化算法：
-
机器学习基本流程：
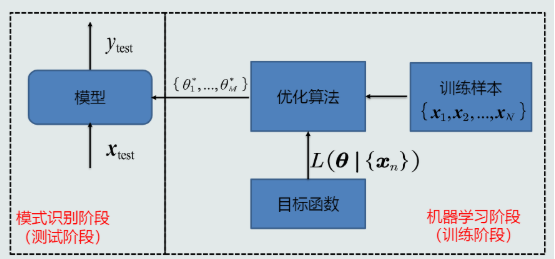
- 输出真值（标签）&标注：
-
机器学习的方式：
(1) 监督式学习
(2) 无监督式学习
(3) 半监督式学习
(4) 强化学习
-
测试集&训练集：
-
测试误差&训练误差：
-
模型的泛化能力：
(1) 泛化能力：训练得到的模型不仅要对训练样本具有决策能力，也要对新的（训练过程中未看见的）模式具有决策能力。
(2) 过拟合(over-fitting)：模型训练阶段表现很好，但是在测试阶段表现很差。模型过于拟合训练数据。
(3) 提高泛化能力（防止过拟合的方法）：①选择复杂度适合的模型，②正则化，在目标函数中加入正则项。
-
调参：
调参指的是调整模型中的超参数，模型中的参数（非超参数）是通过机器学习算法得到的，而超参数则需要手动设定。
-
评估方法：
评估方法可以用于选择确定超参数。在训练阶段，从训练集中留出一部分作为验证集，剩下的用于训练，而验证集作为测试集。
(1) 留出法
(2) K交叉验证
(3) 留一验证（特殊的K折交叉验证）
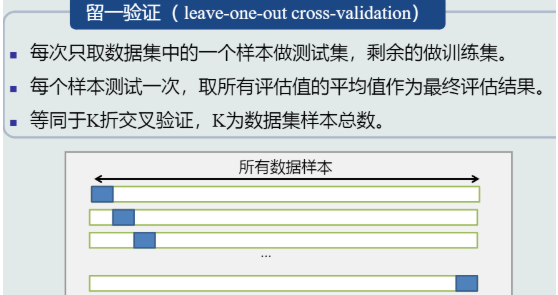
- 模型的性能度量指标：
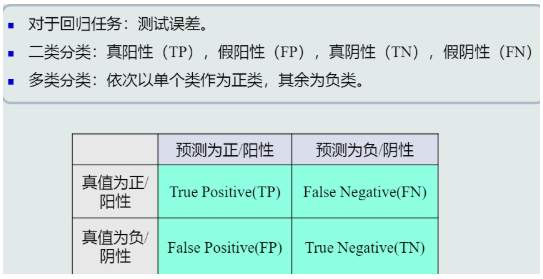
(1) 准确度(Accuracy)：将阳性和阴性综合起来度量识别正确的程度。
(2) 精度(Precision)：预测为阳性样本的准确程度。也叫作查准率。
(3) 召回率(Recall)：全部阳性样本中被预测为阳性的比例。也叫作敏感度。
(4) F-Score：
(5) F1-Score：
(6) 混淆矩阵(Confusion Matrix)：
(7) 曲线度量：
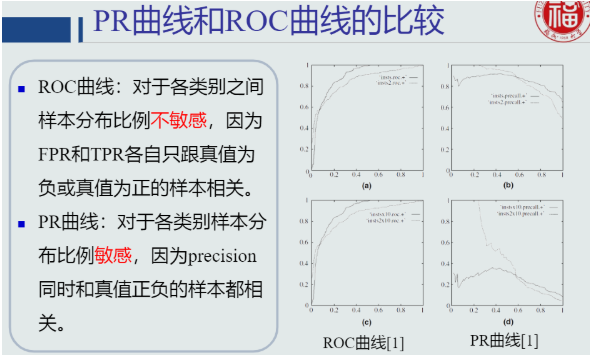
a. PR曲线
b. ROC曲线
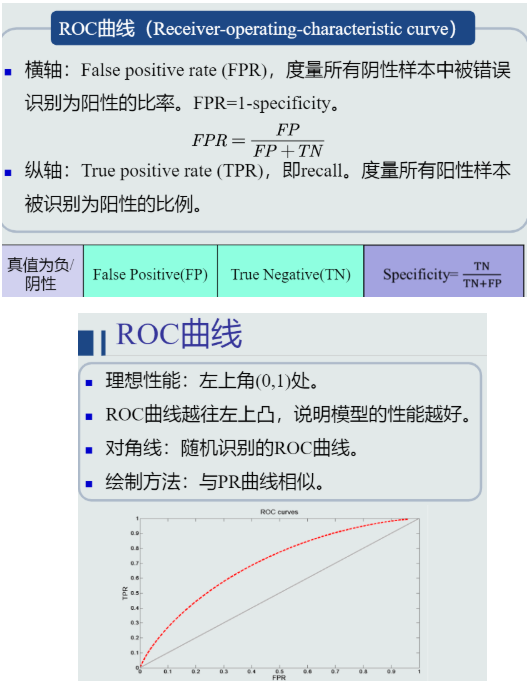
c. PR曲线与ROC曲线的比较
d. AUC曲线
第二章 基于距离的分类器
-
定义
把测试样本到每个类之间的距离作为决策模型，将测试样本判定为与其距离最近的类。
-
判别公式
-
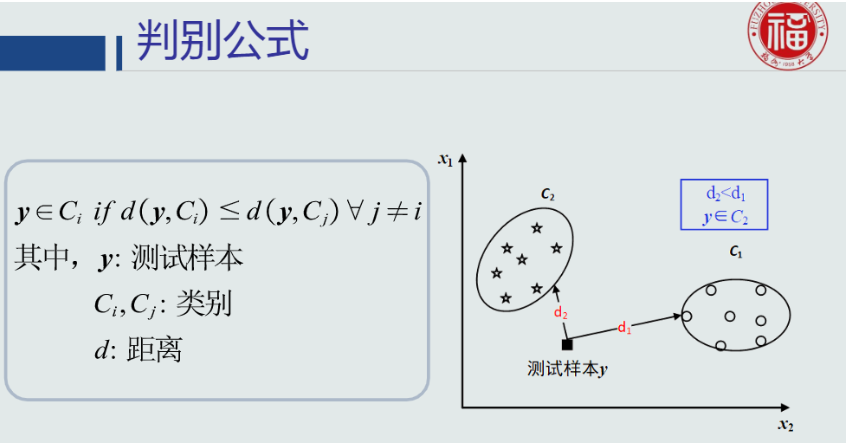
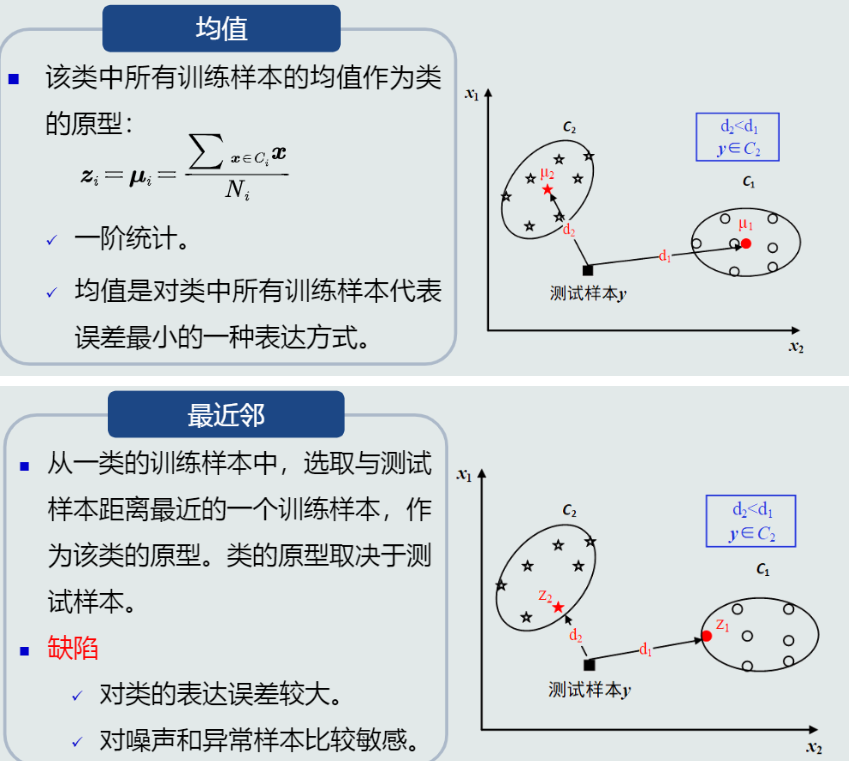
类的原型
(1) 概念：用来代表这个类的一个模式或一组量，便于计算该类和测试样本之间的距离
(2) 种类：均值、最近邻等
-
距离度量
计算测试样本到类的何种距离
(1) 距离度量标准
(2) 常见的几种距离度量
一、MED分类器
-
最小欧式距离分类器(Minimum Euclidean Distance Classifier)
-
距离度量：欧氏距离
-
类的原型：均值
-
目标(对于二分类问题)：给定两个类C1和C2，计算两个类各自的中心点\(\boldsymbol {\mu_1}\)、\(\boldsymbol {\mu_2}\)，计算测试样本与两个中心点的距离，从而做出相应的决策
-
决策边界：
-
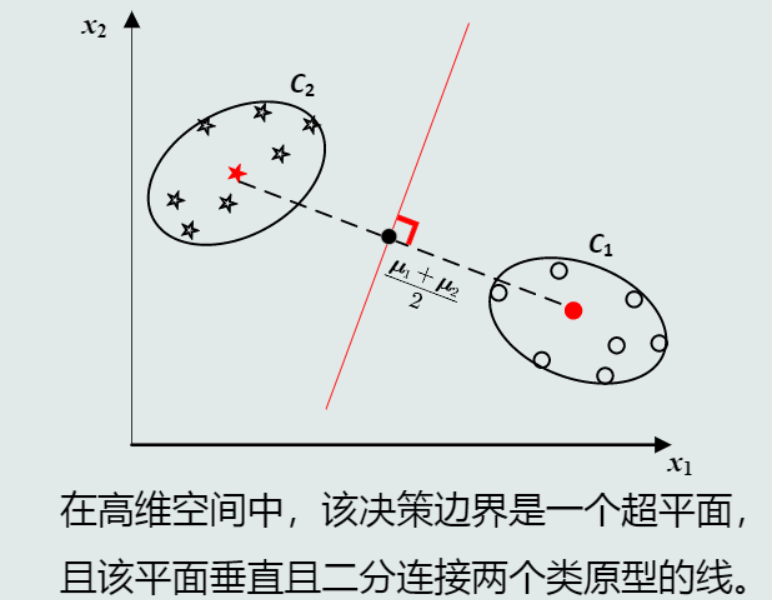
特点：
(1) 平移不变性
(2) 旋转不变性
-
MED分类器(欧氏距离)存在的问题：
(1) 特征的量纲会影响分类结果（样本的协方差矩阵中，对角线元素不相等）
(2) 没有考虑特征之间的相关性（样本的协方差矩阵中，非对角元素不为0）
二、特征白化
-
目的：将原始特征映射到一个新的特征空间，使得在新空间中特征的协方差矩阵为单位矩阵，从而去除特征变化的不同及特征之间的相关性。（消除量纲的影响，去除特征之间的相关性）
-
方法：特征解耦+白化
(1) 解耦：将协方差矩阵对角化，去除特征之间的相关性
(2) 白化：在对角化的协方差矩阵上进行尺度变换，实现所有特征具有相同方差（单位化）
-
公式：
\[\boldsymbol{y} = W\boldsymbol{x} \]其中，\(\boldsymbol{x}\)为原始特征，\(\boldsymbol{y}\)为新特征，\(W\)是映射矩阵。\(W = W_2W_1\)，\(W_1\)用于解耦，\(W_2\)用于白化。
解耦：\(W_1 = \Phi^T\) （\(\Sigma_x\)的特征向量矩阵的转置，\(\Sigma_x\)是\(\boldsymbol{x}\)的协方差矩阵）
白化：\(W_2 = \Lambda^{-\frac{1}{2}}\) （\(\Lambda\)是以\(\Sigma_x\)的特征值作为对角线元素的对角阵，对应于\(\Phi\)）
-
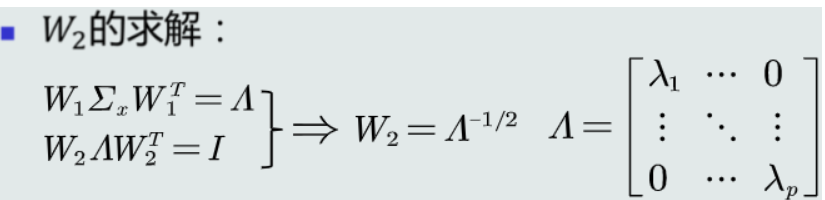
目标结果：
-
几点说明
三、MICD分类器
-
最小类内距离分类器(Minimum Intra-class Distance Classifier)， 基于马氏距离的分类器
-
距离度量：马氏距离
-
类的原型：均值
-
判别公式：
-
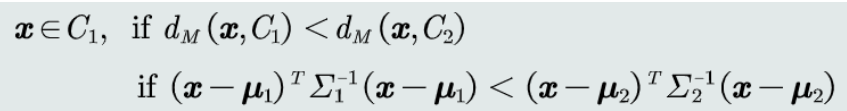
性质：
-
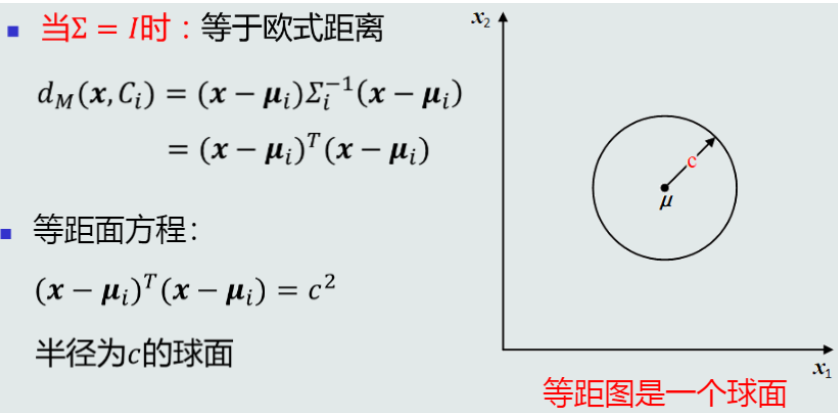
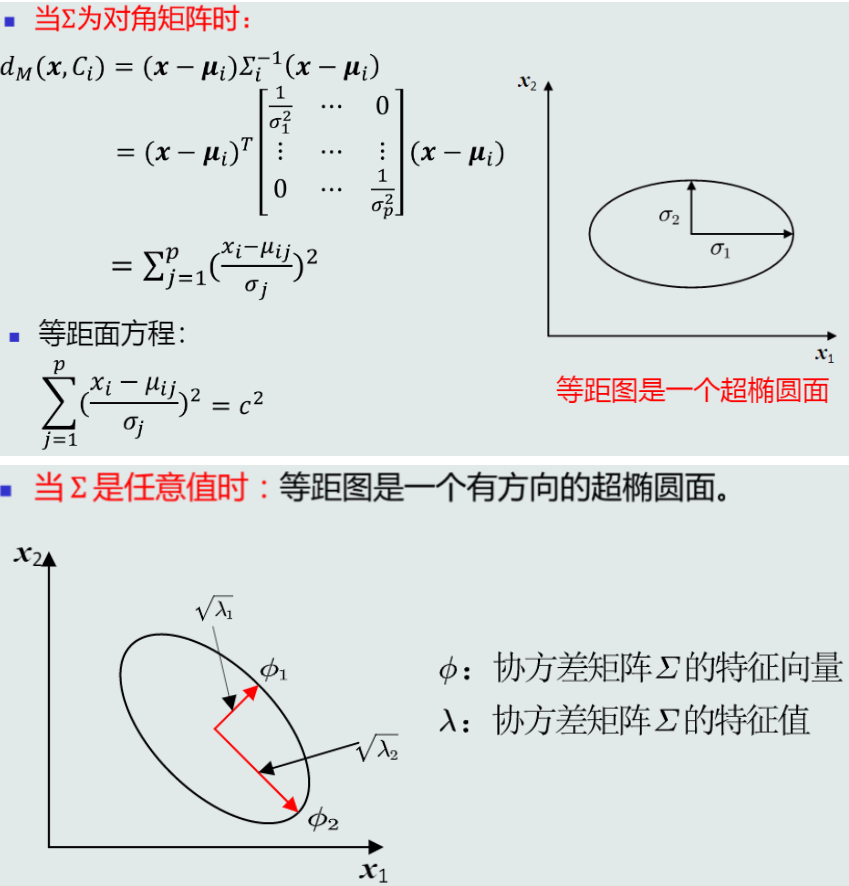
决策边界：
由上述公式可知，决策边界可能是超平面、超球面、超椭球面、超抛物面、超双曲面（取决于\(\Sigma_1\)和\(\Sigma_2\)之间的关系）
-
特点：
具有非奇异线性变换不变性
(1) 平移不变性
(2) 旋转不变性
(3) 尺度缩放不变性
(4) 不受量纲影响
-
MICD分类器的问题：
MICD分类器的错误概率可能大于MED分类器！
第三章 贝叶斯决策与学习
引入概率的观点，考虑类的分布等先验知识，例如，类别之间样本数量的比例，类别之间的相互关系等。经由观测似然修正先验概率，得到后验概率，并用后验概率进行分类决策。有时，还要考虑对不同类别的样本误判造成的后果。
一、MAP分类器
-
最大后验概率(Maximum posterior probability, MAP)分类器
-
目标：将测试样本决策分类给后验概率最大的那个类
-
判别公式：
-
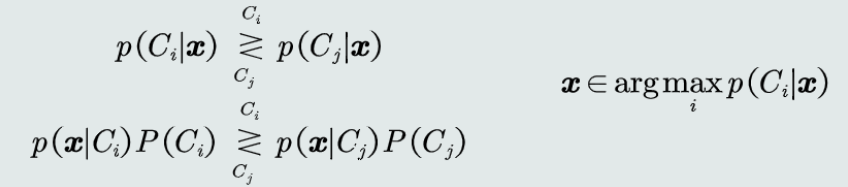
决策边界：
-
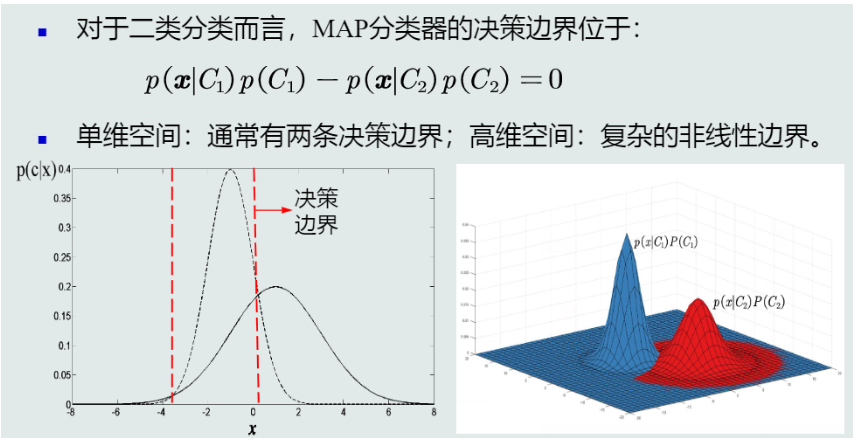
决策误差：
(1) 决策误差的定义：
其中，R1与R2交集为空。
(2) MAP分类器的决策误差：
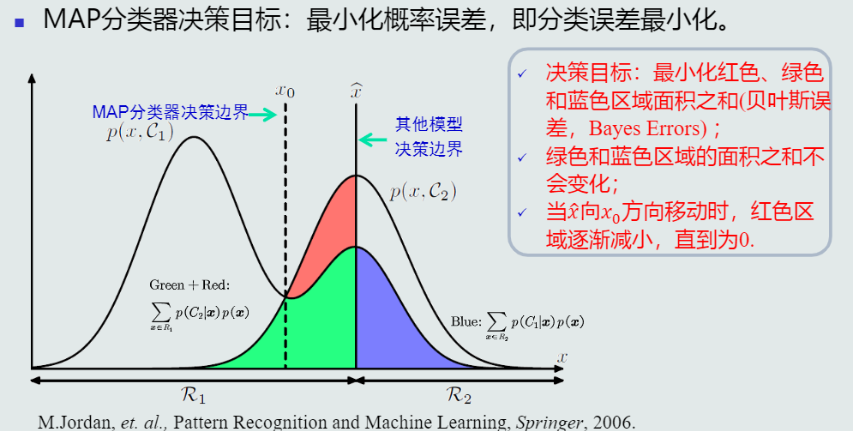
无论如何，两个类别的概率密度分布中重叠的部分一定会出现误判，所以最好的情况就是，在不重叠的部分没有误判，即上图的\(x = x_0\)位置。给定所有测试样本，MAP分类器选择后验概率最大的类，等于最小化平均概率误差，即最小化决策误差。
二、 决策风险
贝叶斯决策不能排除出现误判的情况，由此会带来决策风险。更重要的是，不同的错误决策会产生程度完全不一样的风险。
经典案例：
-
损失的概念：
-
损失/决策风险的评估：
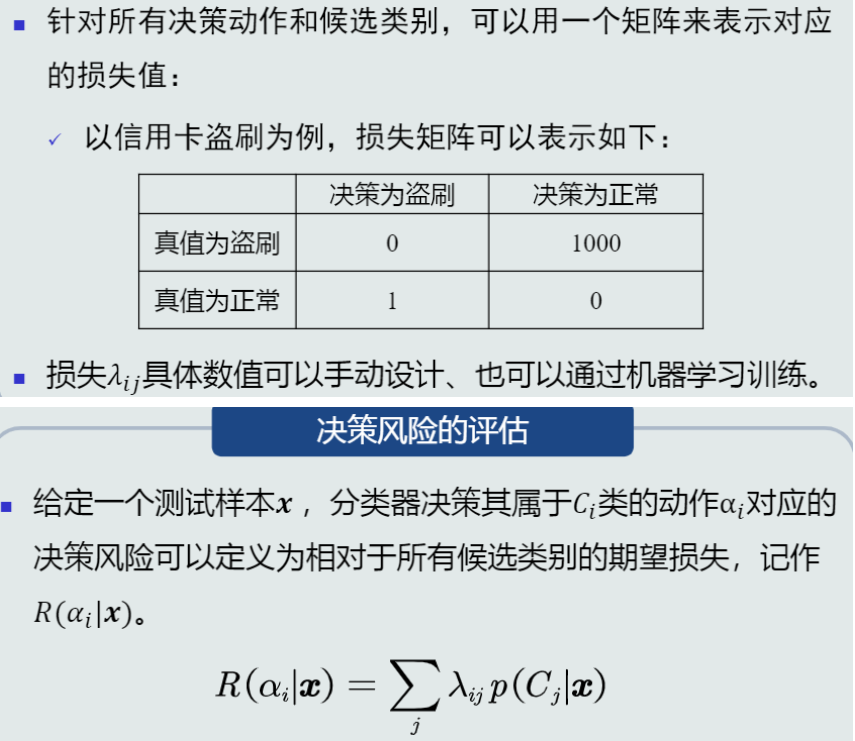
三、贝叶斯分类器(Bayes classifier)
在MAP分类器的基础上，加入决策风险因素，得到贝叶斯分类器。给定一个测试样本\(\boldsymbol {x}\)，贝叶斯分类器选择决策风险最小的类。
-
判别公式：
(1) 二分类：
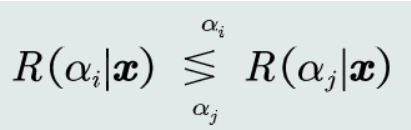
(2) 多分类：
(3) 信用卡盗刷的栗子：
-
贝叶斯分类器的决策损失：
-
决策目标：
-
朴素贝叶斯分类器(Naive Bayes)：
若特征是多维的，则学习特征之间的相关性会很困难。简化问题，假设特征之间是相互独立的，则得到朴素贝叶斯分类器。
-
拒绝选项：
当样本落在决策边界时的处理方法
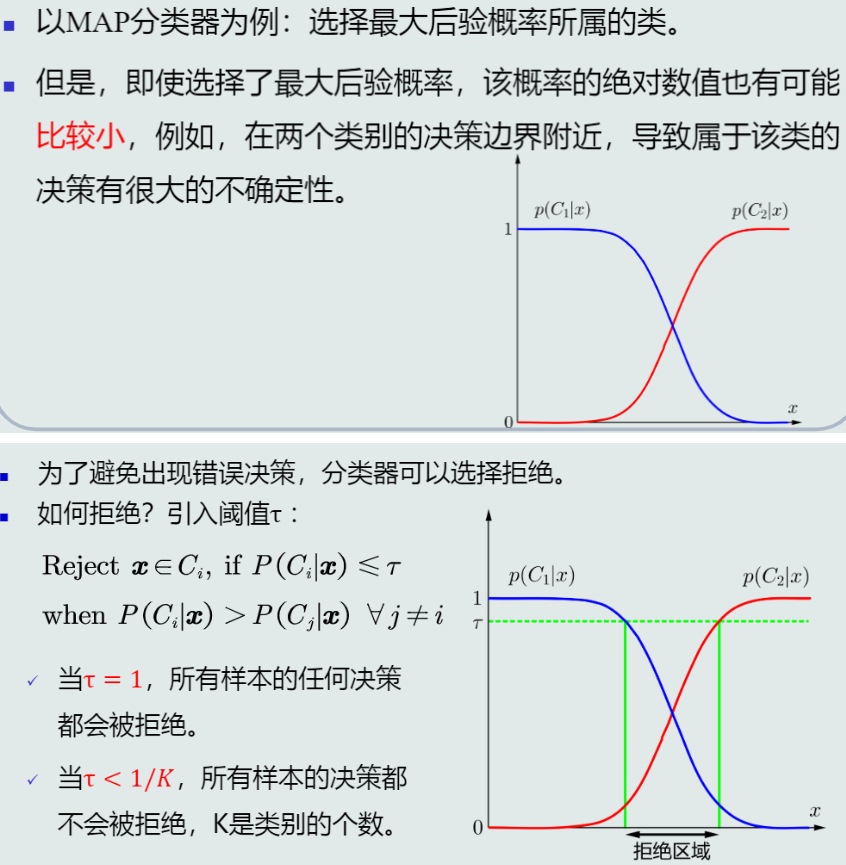
四、先验概率与观测概率的表达
先验概率和观测概率的表达方式：
(1) 常数表达
(2) 参数化解析表达：高斯分布（正态分布）等……
(3) 非参数化表达：直方图、核密度、蒙特卡洛等……
1. 高斯分布（正态分布）
(1) 单维：
(2) 多维：
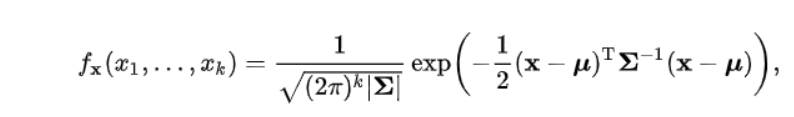
上式中的\(|\Sigma|\)表示协方差矩阵的行列式，\(\Sigma\)是非奇异的，k表示特征维度。
2. 观测概率的确定
(1) 假设观测概率服从单维高斯分布
-
决策边界：
(2) 假设观测概率服从多维高斯分布
- 决策边界：
3. 各分类器判别函数的比较
MAP分类器偏向于先验概率较大、分布较为紧致的类！能够解决MICD分类器的问题（MICD倾向于选择方差较大的类）。
五、先验和观测似然概率的学习
贝叶斯决策中，求取后验概率需要事先知道每个类的先验概率和观测似然概率，这两类概率分布可以通过机器学习算法得到。根据概率分布的表达形式，监督式学习（训练样本的标签是给定的）方法可以通过以下两种方法学习先验和观测似然概率。
-
常用的参数化方法（概率分布形式已知）：
(1) 最大似然估计(Maximum Likelihood Estimation, MLE)：将参数视为确定值
(2) 贝叶斯估计(Bayesian Estimation)：将参数视为随机变量
-
常用的非参数化方法（概率分布形式未知）：
(1) K近邻法(K-nearest neighbors, KNN)
(2) 直方图技术(Histogram technique)
(3) 核密度估计(Kernel density estimation)
1. 最大似然估计
-
定义：
-
估计先验概率：
先验概率的最大似然估计就是该类训练样本出现的频率
-
估计观测概率：
利用最大似然估计方法，计算得到高斯分布均值和高斯分布协方差的估计量如下：
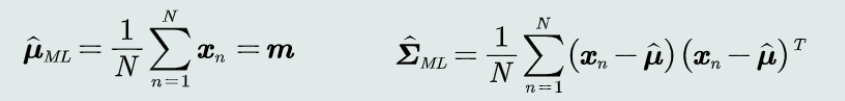
高斯分布均值的最大似然估计等于样本均值，高斯分布协方差的最大似然估计等于所有样本的协方差！
2. 最大似然的估计偏差
-
无偏估计的概念：
-
数学期望和协方差的计算：
-
高斯分布均值和协方差的最大似然估计的无偏性：
3. 贝叶斯估计
-
定义：
这里的参数\(\theta\)表示参数空间的所有参数。
-
高斯观测似然：
-
参数的先验概率：
-
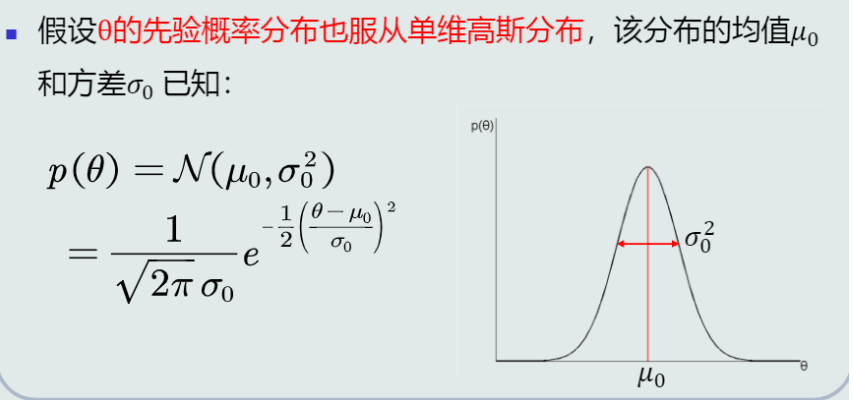
参数的后验概率（对单个类别\(C_i\)而言！）：
在参数的先验概率和观测似然概率分别服从高斯分布\(N(\mu_0, \sigma_0^2)\)和\(N(\mu, \sigma^2)\)的情况下，参数的后验概率也服从高斯分布\(N(\mu_\theta, \sigma_\theta^2)\)。（其中，\(\mu = \theta\)，待估计参数\(\theta\)就是高斯分布的均值\(\mu\)）
当\(C_i\)类的样本个数\(N_i\)足够大时，\(\mu_\theta\)趋向于样本均值，\(\sigma_\theta^2\)趋向于0。
-
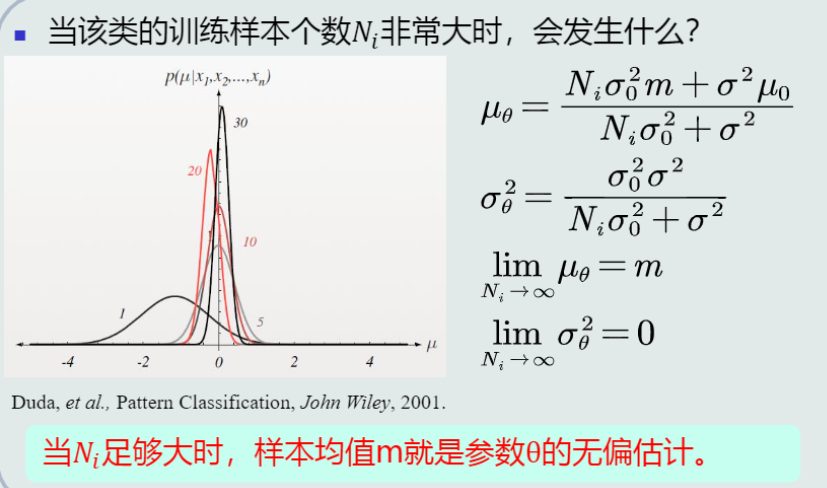
特点：
当训练样本和先验概率取极值时，从后验概率的极限值可以看出，贝叶斯估计具有不断学习的能力。
-
参数的后验概率应用于MAP分类：
给定训练样本、参数的先验概率、观测似然的分布形式，通过贝叶斯估计来估计观测似然概率，进而可以得到样本\(\boldsymbol {x}\)属于类\(C_i\)的后验概率用于决策。
-
贝叶斯估计与最大似然估计比较：
4. 概率密度估计基本理论
概率密度估计的重要公式：\(p(\boldsymbol{x}) \approx \frac{k}{NV}\)。
(1) KNN估计：固定k，求V
(2) 直方图估计：固定V，求k
(3) 核密度估计（KNN与直方图的折中）：固定V的大小，V的位置不固定，求k
上面三种方法都分为两个阶段：统计学习阶段与概率密度估计阶段。
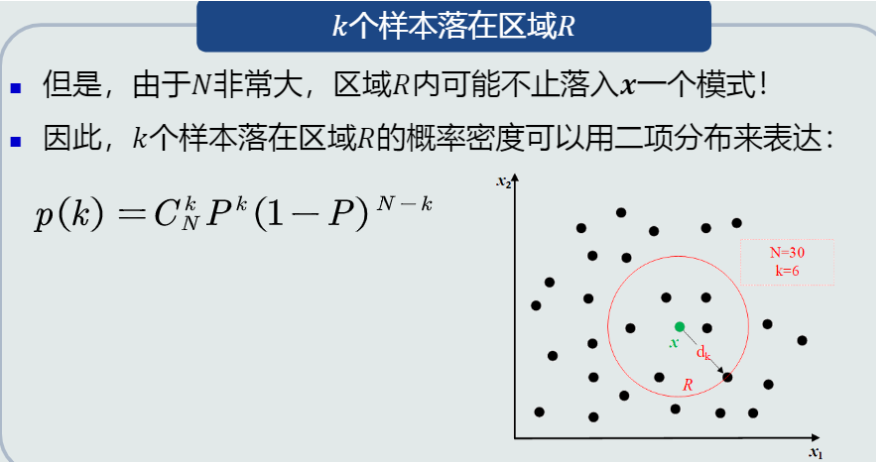
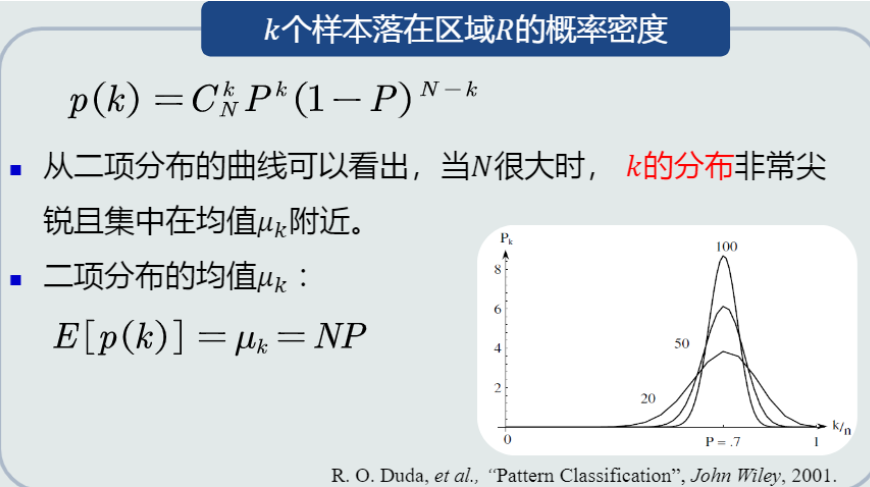
5. K近邻(KNN)估计
- KNN分类器（基于KNN估计的MAP分类器）：
-
优点：
(1) 可以自适应的确定\(\boldsymbol{x}\)相关的区域R的范围
-
缺点：
(1) KNN概率密度估计不是连续函数
(2) 不是真正的概率密度表达，概率密度函数的积分是\(\infin\)，而不是1
(3) 在测试阶段，仍然需要存储训练样本
(4) 区域R由第k个近邻点确定，易受噪声影响
6. 直方图估计
-
优点：
(1) 固定区域R，减少由于噪声影响造成的估计误差
(2) 不需要存储训练样本
-
缺点：
(1) 固定区域R的位置，意味着当前格子不是以样本\(\boldsymbol{x}\)为中心，导致统计和概率估计不准确
(2) 固定区域R的大小，缺乏概率估计的自适应能力，导致概率密度函数过于尖锐或平滑
-
双线性插值（直方图估计的优化）：
\(\boldsymbol{x}\)向相邻两个格子都贡献一部分k值（和为1），与格子中心越近则贡献越多。
-
带宽h的选择：
不宜过大，也不宜过小
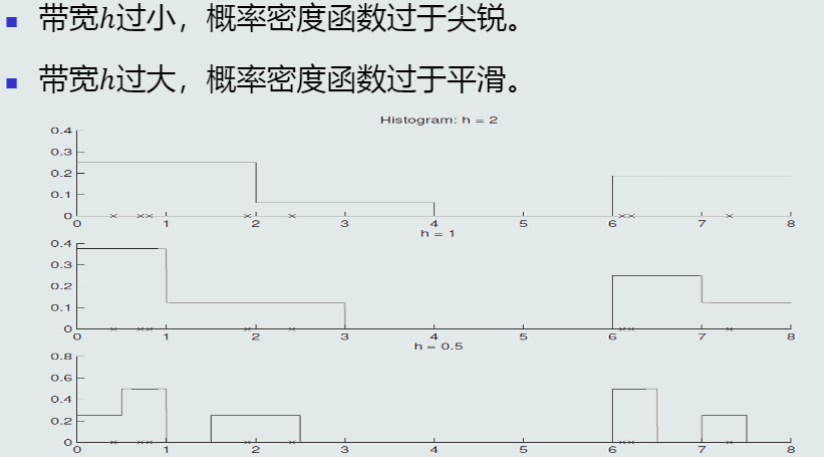
7. 核密度估计
KNN估计与直方图估计各有优缺点，且他们共同的缺点是概率密度估计不连续，不符合概率密度函数的定义。核密度估计在一定程度上结合了KNN与直方图的优点。
核密度估计中，区域R是一个单位超立方体，由核函数来确定，核函数可以是高斯分布、均匀分布、三角分布等，但核函数必须是对称函数。当选择的核函数是连续函数（比如高斯核函数）时，估计的概率密度是连续的。
-
优点：
(1) 以待估计样本\(\boldsymbol{x}\)为中心、自适应确定区域R的位置（类似KNN）
(2) 适用所有训练样本，而不是基于第k个近邻点来估计概率密度，从而克服KNN估计存在的噪声影响
(3) 若核函数是连续的，则估计的概率密度函数也是连续的
-
缺点：
(1) 与KNN估计一样，在测试阶段，核密度估计也需要存储所有训练样本
-
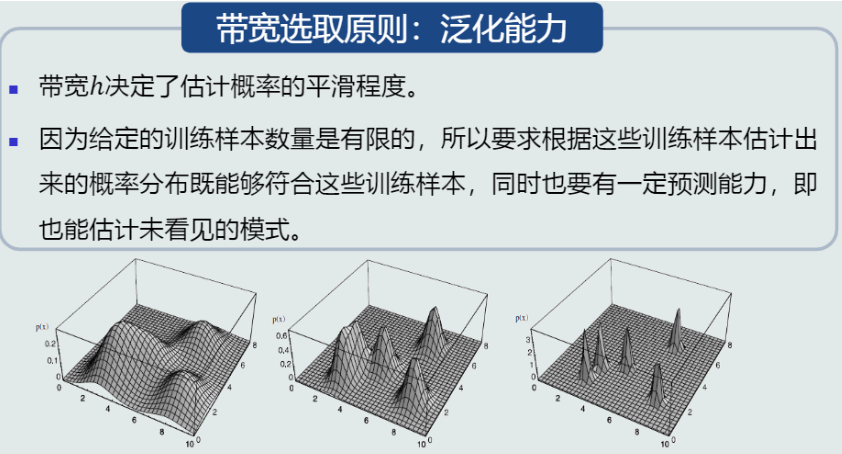
带宽选择：
带宽h决定了估计概率的平滑程度，选取带宽的原则是泛化能力的好坏
