利用python进行数据分析-第四章笔记
Chapter 4 NumPy Basics: Arrays and Vectorized Computation
题外话:numpy short for numerical python 😃
Ndarray: A Multidimensional Array Object
ndarray: short for N-dimensional array object. 一个最直观的优点是可以直接操作整个 ndarray 的元素而不必使用 for loop。
尽量使用
import numpy as np
np.function()
防止 python 的内置函数与 numpy 中给出的函数产生冲突。
- Creating ndarrays
一些常用方法:
# 1
# params: any sequence-like object
np.array()
# 2
# params: shape(tuple)
np.zeros((1,2))
np.ones((2,3))
np.empty((3,4))
# 3
# params: range(int), like python built-in range
np.arange(15)
顺便可以在创建时,规定数据类型:np.array([1,2,3,4,5], dtype=np.float64)
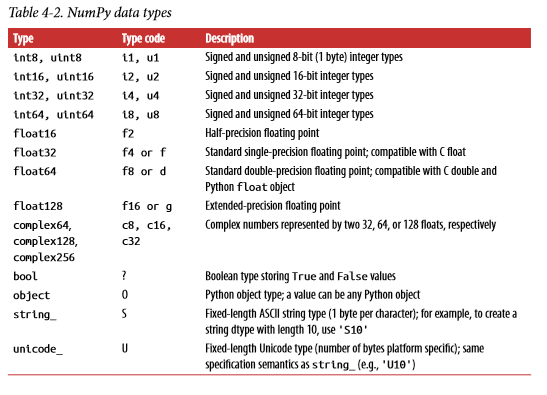
还可以使用astype对已有的 array 进行数据类型的转换:
arr = np.array([1,2,3])
arr1 = arr.astype(np.float64)
# 字符串如果无法转换成相应的数据类型会 ValueError
arr2 = np.array(['1.2', '2.3'])
arr3 = arr2.astype(np.float)
- Arithmetic with NumPy Arrays
Arrays are important because they enable you to express batch operations on data without writing any for loops. NumPy users call this vectorization. Any arithmetic operations between equal-size arrays applies the operation element-wise.
需要注意的是,arr * arr 的运算是 element-wise 的,即各位置相应元素相乘,也就是说不是矩阵之间的运算。
Operations between differently sized arrays is called broadcasting and will be discussed in more detail in Appendix A.
- Basic Indexing and Slicing
对于一维的 ndarray,slicing 操作与 list 的 slicing 很类似,但是需要重点关注不同点:
- ndarray 支持 broadcast 操作,例如
ndarray[3:7]=12是允许的,但是在 list 上就不可以; - 最重要的,ndarray 不会对 slicing 的切片进行 copy,也就是说对 slicing 的一切修改会反映在原 ndarray 上:
a = np.array([1,2,3,4])
arr = a[1:4]
arr[:] = 43
print(arr)
print(a)
这种设计的原因是顾虑 numpy 在处理大规模数据时的效率问题。
If you want a copy of a slice of an ndarray instead of a view, you will need to explicitly copy the array—for example, arr[5:8].copy().
对于二维和更高维的 ndarray,slicing 就相对难理解一些,一个较好理解的方式是从外向里,例如:
arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
arr3d[0] # = [[1, 2, 3], [4, 5, 6]]
arr3d[0,1] # = [4, 5, 6]
arr3d[:2, 1:] # = [[[4,5,6],[10,11,12]]]
- Boolean Indexing
这个性质就是 mask 的实现基础。直接看代码好理解一些。
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
data = np.random.randn(7, 4)
data[names == 'Bob'] # = [data[0], data[3]]
也可以在data[names == 'Bob']里指定列的序号,同时可以使用更复杂的 bool 表达式来表示条件。也可以结合之前 slicing 的 broadcast 性质进行赋值。
- Fancy Indexing
顾名思义,这种方式十分 fancy 😃
arr = np.arange(32).reshape((8,4))
arr[[0,1,2,3]]
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]
# [12 13 14 15]]
index 是负数的时候从后向前,与 list 的 index 类似。
还有两个比较复杂的例子:
arr[[1, 5, 7, 2], [0, 3, 1, 2]]
# arr[1,0], arr[5,3], arr[7,1], arr[2,2], array([ 4, 23, 29, 10])
arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]
# array([[ 4, 7, 5, 6],[20, 23, 21, 22],[28, 31, 29, 30],[ 8, 11, 9, 10]])
- Transposing Arrays and Swapping Axes
对于二维的 ndarray,Transposing 就是我们常说的矩阵转置,对于更高维的 ndarray,transpose 可能不是那样直观,但是只要记住转置的定义是a[dimension_1][dimension_2] = a[dimension_2][dimension_1]即可。
arr = np.arange(16).reshape((2,2,4))
arr.transpose((1,0,2))
# array([[[ 0, 1, 2, 3],[ 8, 9, 10, 11]],
# [[ 4, 5, 6, 7],[12, 13, 14, 15]]])
对于那些一步得不到的转置,会通过多次转置的方式得到:
arr = np.arange(32).reshape((4,2,2,2))
print(np.transpose(arr, (1,3,2,0)))
# a: 0 1 2 3
a = np.transpose(arr, (1,0,2,3))
# a: 1 0 2 3
a = np.transpose(a, (0,3,2,1))
# a: 1 3 2 0
print(a)
.T运算符是一个 transpose 的简单形式,对于二维的 ndarray, .T就表示矩阵的转置,而对于多维的 ndarray,.T算符的规则是:
a.shape # = (d0, d1, d2, d3, ..., dn)
a.T.shape # = (dn, ..., d2, d1, d0)
swapaxes方法与 transpose 和.T算符类似,不同的是只支持两个维度的转换:
arr.swapaxes(axis1, axis2)
注意:
swapaxes similarly returns a view on the data without making a copy.
这里涉及到 view 和 copy 的区别,其实有点类似于 C++ 中的引用,先看一段代码:
arr = np.arange(32).reshape((4,2,2,2))
print(arr)
print(arr.transpose(3,1,2,0))
brr = arr.swapaxes(3,0)
brr[0,0,0,0] = 111111
brr[0,0,0,1] = 222222
print(arr)
print(brr)
这里的 brr 就是 arr 的一个 view,个人的理解是 brr 的每个位置上存的都是 arr 中每个元素的 view(类似于引用),修改 brr 的同时就直接把 arr 的相应位置的值也都修改了。
Universal Functions: Fast Element-Wise Array Functions
A universal function, or ufunc, is a function that performs element-wise operations on data in ndarrays.
一些常用的一元 ufunc,详细的参数信息可以查看 numpy 文档:

常用二元 ufunc:


Array-Oriented Programming with Arrays
这部分讲了一些不用 for loop 进行 ndarray 计算的实例。
- 使用 meshgrid 构造坐标点矩阵计算多个点间距离
x, y = np.meshgrid([1,2,3],[-1,-1.5,-2])
print(x, y)
x 和 y 的相应位置表示一个点的横纵坐标,如果把图像画出来是这样的:
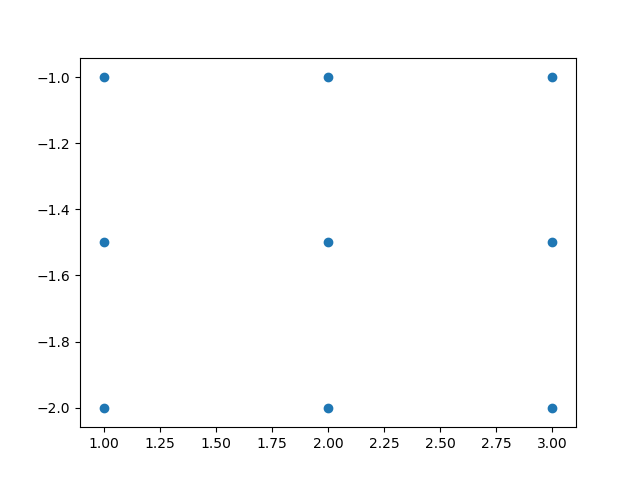
所以计算距离就可以使用:
z = np.sqrt(x ** 2 + y ** 2)
顺便书中还把距离的灰度图画了出来,可以参考一下。
- Expressing Conditional Logic as Array Operations
主要讲了 numpy.where() 的使用。
用法是:np.where(arr > 0, 2, -2),即 arr 中大于0的元素赋值为2,否则赋值为-2。
where 的文档是这么描述的:
where(condition, x=None, y=None, /)
param condition
where(condition, [x, y])
Return elements, either fromxory, depending oncondition.
If onlyconditionis given, returncondition.nonzero().
Parameterscondition : array_like, bool
When True, yieldx, otherwise yieldy.
x, y : array_like, optional
Values from which to choose.x,yandconditionneed to be
broadcastable to some shape.
发现 condition, x 和 y 其实都是 array-like 的形式,这里其实是有 broadcast 的支持。
- Mathematical and Statistical Methods
一些简单的统计方法。

解释一下:
cumsum 和 cumprod 的 axis 参数表示计算累加和(积)的轴,axis = 0 表示第一个维度,也就是直观上的从上到下计算累加和(积),而不是表示对第几维的元素做累加和(积)。即 axis 表示方向。
- Methods for Boolean Arrays
boolean arrays 也是 ndarray,所以相应的统计方法都适用,同时还有bools.any()和bools.all()两个方法,类似于集合运算中的并和交。
- Sorting
这里 numpy 的 sort 和 python 内置的 sort 很类似,numpy 的 sort 可以规定 axis。需要注意的是np.sort()返回的是一个 copy,而arr.sort()是在原地修改 arr 的值,没有返回值。
arr = np.random.randn(5,3)
print(arr)
brr = np.sort(arr, axis=1)
print(brr)
print(arr)
arr.sort(1)
print(arr)
- Unique and Other Set Logic
对于一维的 ndarray,numpy 提供了一些独有的方法。

File Input and Output with Arrays
np.save()和np.load()
- input:
np.load(file_path) - output:
np.save(file_name, arr)
np.savez(file_name, a=arr, b=brr)
np.savez_compressed(file_name, a=arr, b=brr)
有个问题是如果我想存100个甚至更多的 ndarray 怎么办?
Linear Algebra
一些简单的线性代数用法:


分别解释一下:
- diag:返回方阵的对角元素,或者根据一个1维的 ndarray 返回一个对角阵。
- dot:返回矩阵的内积
- trace:返回矩阵的 trace(对角元素和)
- det:返回矩阵的行列式
- eig:计算矩阵的特征值和特征向量
- inv:计算矩阵的逆,不成功时抛出 LinAlgError
- pinv:计算矩阵的伪逆
- qr:求矩阵的 qr 分解
- svd:求矩阵的奇异值分解
- solve:求解线性方程组
- lstsq:求出线性方程组的最小二乘解
Pseudorandom Number Generation
python 内置的 random 比 numpy 的 random 慢。
下面是一些基本用法:

注意:
- python 内置的 random.randint(a, b) 的范围是 [a, b],而 numpy.random.randint(a, b) 的范围是 [a,b)
Example: Random Walks
用纯 python 的写法:
import random
position = 0
walk = [position]
steps = 1000
for i in range(steps):
x = random.randint(0,1)
print(x)
step = 1 if x else -1
position = position + step
walk.append(position)
plt.plot(walk[:100])
plt.show()
用 numpy 的写法:
arr = np.random.randn(1000,)
step = np.where(arr > 0, 1, -1)
walk = step.cumsum()
而且可以同时进行多次的随机游走,只需要让 arr 是一个二维矩阵即可:
arr = np.random.randn(3,1000)
step = np.where(arr > 0, 1, -1)
walk = step.cumsum(axis=1)
对 walk 使用统计方法可以对某次随机游走进行分析。
结果如下:
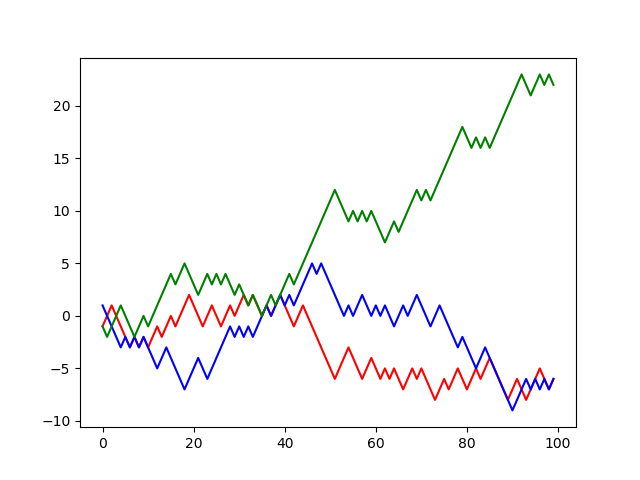
Conclusion
While much of the rest of the book will focus on building data wrangling skills with pandas, we will continue to work in a similar array-based style. In Appendix A, we will dig deeper into NumPy features to help you further develop your array computing skills.

