算法复习-分支限界法
基本思想

对于优化问题,要记录一个到目前已经取得的最优可行解及对应的目标函数值,这个记录要根据最优的原则更新。无论采用队列式还是优先队列式搜索,常常用目标函数的一个动态界(函数)来剪掉不必要搜索的分枝。
对于最大值优化问题,经常会估计一个(动态)上界,如果当前节点的估计(动态)上界\(CUB\)小于当前取得的目标值,就直接剪掉该节点的子树。
对于最小值优化问题,经常会估计一个(动态)下界,如果当前节点的估计(动态)下界\(CLB\)大于当前取得的目标值,就直接剪掉该节点的子树。
对于可行解问题,经常会估计一个(动态)下界,如果当前节点的估计(动态)下界\(CLB\)大于当前取得的目标值,就直接剪掉该节点的子树。
上面的动态上下界就叫做剪枝函数,可以有效地减少活节点数,降低复杂度。
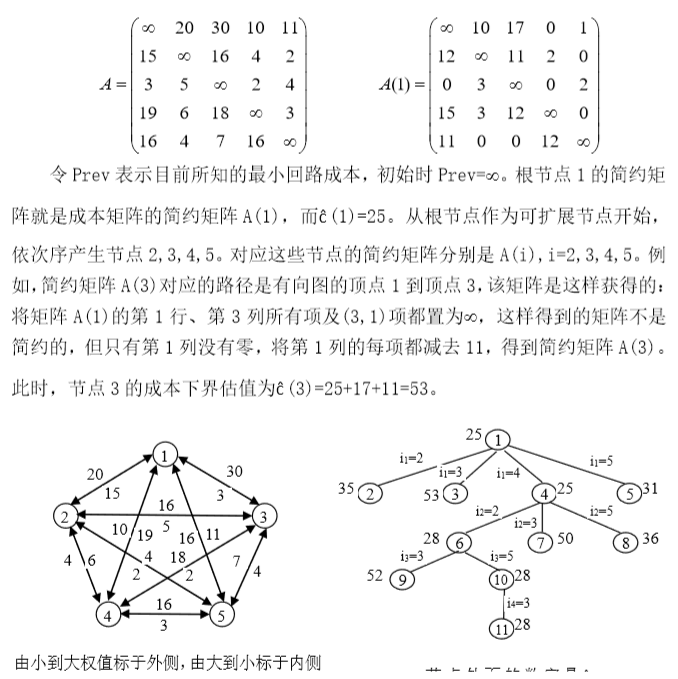
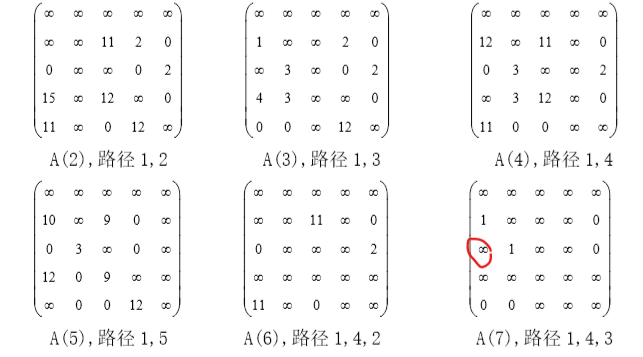
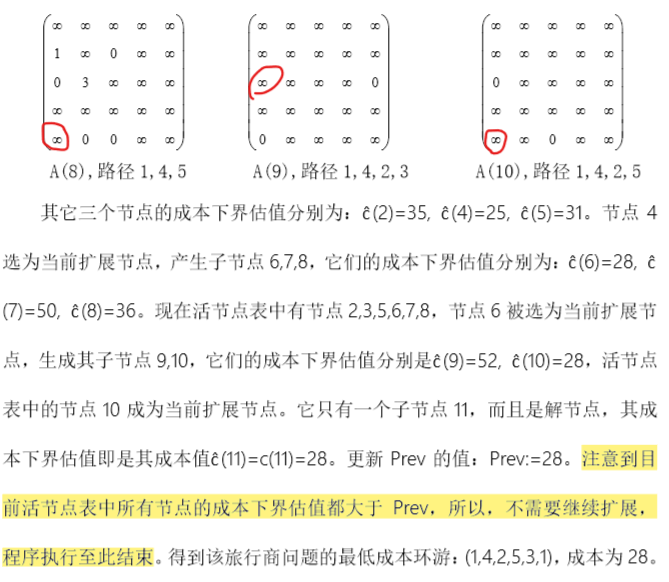
旅行商问题
状态空间树:
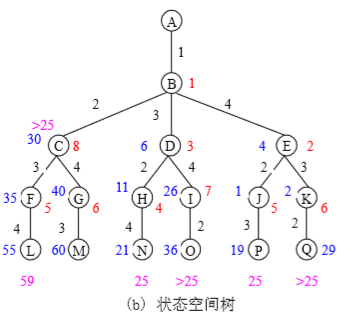
队列分支限界法:

优先队列分支限界法:


0/1背包的分支限界法

分别解释节点各个字段的含义:
- Parent:表示节点X的父亲节点;
- Level:表示节点X在状态空间树中的深度;
- Tag:表示每个物品的选择与否;
- CC:记录背包在节点X处的可用容量;
- CV:记录在节点X处的物品价值;
- CUB:存放节点X的动态上界Pvu;
各个变量的含义:
- Pvu(X):表示节点X处可行解所能达到的一个上界;
- Pvl(X):表示节点X处可行解所能达到的一个下界;
- prev:表示目前能得到的最大值。
剪枝方案:
如果Pvu<prev,那么直接剪掉节点X的子树,不将X放入活节点表,或者说不生成X的子节点。只用这个策略其实就可以完成这个任务,但是我们想要尽可能多的降低复杂度,接着看。
如果Pvu=prev,因为prev可能是一个方案的结果,那么这是从X继续搜索下去不会得到更好的解,可以剪掉;但是如果prev不是一个答案节点,而是一个中间结果,那么问题就复杂了。
我们先来看prev的更新过程,对于一个节点X,\(prev=max(prev, Pvl(X))\),我们发现,prev有一定的“前瞻性”,就是说如果在估计Pvl的时候恰好就是答案节点的解,那么prev将会在到达答案节点前就获知当前路径的结果,那么这个时候我们如果认为prev=Pvu的时候就直接剪掉的话,就会遗失可能的最优解。
那么自然地我们就想要破除prev的前瞻性,也就是说让prev只在答案节点处得到最后的结果,所以我们用一个足够小的常量e,把prev的更新过程改为\(prev=max(prev, Pvl(X)-e)\),这样就规避掉了prev的前瞻性。那么e到底应该多小,只要不影响两个节点之间的优先级顺序就可以,即\(Pvl(Z)<Pvl(Y)=>Pvl(Z)<Pvl(Y)-e\)。
那么经过上述处理,最终的剪枝策略是:当\(Pvu \le prev\)时剪掉节点X。同时Pvu(X)可以作为优先级函数。
代码如下,在AcWing上提交通过,需要注意的细节都写在注释里了,还是很多的:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int MAX = 1010;
// e的值也不能太小,要在double精度内
const double e = 0.0001;
int n, M;
int res = 0;
int W[MAX];
int P[MAX];
double PW[MAX];
struct node
{
struct node *parent, *lchild, *rchild;
int level, tag, cc;
double cub, cv;
node(int _level, int _tag, int _cc, double _cv, double _cub, node* _left, node* _right, node* _parent)
{
level = _level;
tag = _tag;
cc = _cc;
cv = _cv;
cub = _cub;
lchild = _left;
rchild = _right;
parent = _parent;
}
};
typedef struct node Node;
struct Nodeless
{
bool operator()(const struct node *_left, const struct node *_right)
{
return _left->cub < _right->cub;
}
};
void LUBound(int cap, double cv, int clevel, double &Pvl, double &Pvu)
{
// 物品需要按照单位价值非递减的方式排列
// 使用完全背包问题的贪心算法估计上下界
Pvl = cv;
int rv = cap;
for (int i = clevel + 1; i <= n; i++)
{
// 至少一个物品无法装入
if (rv < W[i])
{
Pvu = Pvl + rv * 1.0 * P[i] / W[i];
for (int j = i + 1; j <= n; j++)
{
if (rv >= W[j])
{
rv -= W[j];
Pvl += P[j];
}
}
// 此时Pvu >= Pvl,因为物品按照单价从高到低排列
return;
}
rv -= W[i];
Pvl += P[i];
}
// 表示都能装进去
Pvu = Pvl;
return;
}
void Finish(Node* res)
{
int v = 0;
for (int i = n; i > 0; i--)
{
if (res->tag == 1)
{
v += P[i];
}
res = res->parent;
}
cout << v << endl;
}
void LFKNAP()
{
priority_queue<Node*, vector<Node*>, Nodeless> livenodes;
double Pvu, Pvl, prev;
LUBound(M, 0, 0, Pvl, Pvu);
Node* root = new Node(0, 0, M, 0, Pvu, nullptr, nullptr, nullptr);
Node* ans = root;
prev = Pvl - e;
while (root->cub > prev)
{
int i = root->level + 1;
int cap = root->cc;
// 因为cv要和prev比较大小,虽然C++会自动将int升为double,但是写的清楚些总没坏处hhh
double cv = root->cv;
if (i == n + 1)
{
if (cv > prev)
{
prev = cv;
ans = root;
}
}
else
{
if (cap >= W[i])
{
// 为什么不调用LUBound(cap - W[i], cv + P[i], i, Pvl, Pvu)?
// 因为左孩子可行时,Pvu的值等于root->cub,Pvl的值等于之前节点的Pvl,不必再次计算。
// 为什么左孩子里没有更新prev?
// 因为prev=max(prev, Pvl-ee),prev就是各节点Pvl-ee的最大值,这里算出的Pvl一定等于之前节点的Pvl。所以不必计算。
Node* left = new Node(i, 1, cap - W[i], cv + P[i], root->cub, nullptr, nullptr, root);
// 如果只求结果,这里root->lchild=left操作以及下面的root->rchild=right实际上可以省略
root->lchild = left;
livenodes.push(left);
}
LUBound(cap, cv, i, Pvl, Pvu);
if (Pvu > prev)
{
// 这里是个大坑!!!课件上给的是Pvl,应该是Pvu,可在https://www.acwing.com/problem/content/2/测试
Node* right = new Node(i, 0, cap, cv, Pvu, nullptr, nullptr, root);
root->rchild = right;
prev = max(prev, Pvl - e);
livenodes.push(right);
}
}
if (livenodes.empty()) break;
root = livenodes.top();
livenodes.pop();
}
Finish(ans);
}
void quicksort(int start, int end)
{
if (start > end) return;
int i = start, j = end + 1;
double pivot = PW[start];
while (true)
{
while (PW[++i] > pivot && i < end);
while (PW[--j] < pivot && j > start);
if (i < j)
{
swap(W[i], W[j]);
swap(P[i], P[j]);
swap(PW[i], PW[j]);
}
else break;
}
swap(W[j], W[start]);
swap(P[j], P[start]);
swap(PW[j], PW[start]);
quicksort(start, j - 1);
quicksort(j + 1, end);
}
int main()
{
cin >> n >> M;
for (int i = 1; i <= n; i++)
{
cin >> W[i] >> P[i];
PW[i] = 1.0 * P[i] / W[i];
}
quicksort(1, n);
LFKNAP();
return 0;
}
使用队列式的分支限界法只需要LFKNAP方法中while(root->cub > prev)改为while(true),然后改用普通的queue就可以了。
这个算法的时间复杂度暂时还不会分析QAQ,我觉得最坏是\(O(2^n)\),但是经过剪枝策略后平均的时间复杂度应该要更小。
有耐心的朋友可以把搜索树打出来看看,我是没耐心了QAQ,这个课件的打印错误没把我命要了。。。
还是顺手补上了这个搜索树的代码,用的是BFS的思路:
void layerOrder(Node* root)
{
cout << "Search Tree: " << endl;
queue<Node*> q;
q.push(root);
int layer = 0;
int cnt = 0;
while(!q.empty())
{
cout << "layer: " << layer;
if(layer > 0)
cout << " weight: " << W[layer] << " price: " << P[layer] << endl;
else cout << endl;
int layer_len = q.size();
cnt += layer_len;
for(int i = 0 ; i < layer_len ; i++)
{
Node* cur = q.front();
q.pop();
cout << "node: " << cur << " parent: " << cur->parent;
cout << " tag: " << cur->tag << endl;
if(cur->lchild) q.push(cur->lchild);
if(cur->rchild) q.push(cur->rchild);
}
layer++;
}
cout << "Size of Tree Nodes: " << cnt << endl;
}
既然做了这部分修改,那就再来比较一下队列式和优先队列式的搜索节点数量:
对于用例
队列式的搜索树长这样:

优先队列的搜索树长这样:
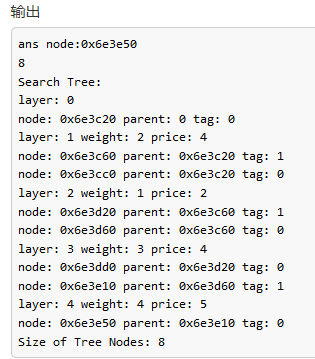
可见队列式的节点数是10,优先队列的节点数是8,而且是在输入用例规模这么小的情况下,所以我们可以说优先队列可以更好的降低分支限界法的搜索复杂度。
电路板布线问题
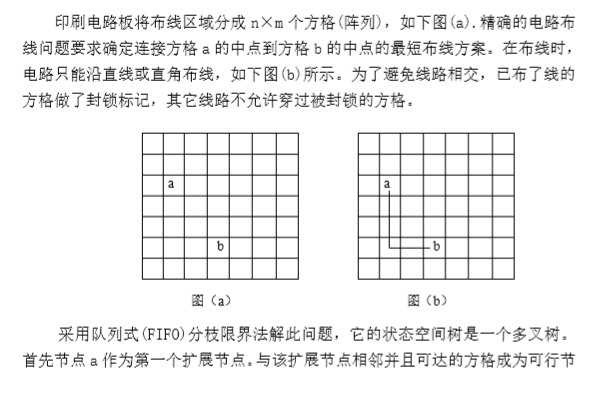

找最短路径就从目标节点开始,每次找长度减一的节点进入即可,直到找到开始节点,这个策略是一定可以找到开始节点的,就是说在回溯过程中不会走到错误的路径上。
如果不存在最短路径,那么活节点表会变空,所以直接输出无解即可。
由于每个活节点最多进入活节点队列一次,最多需要处理mn个节点,扩展一个活节点需要\(O(1)\)的时间,所以共耗时\(O(mn)\)。构造最短路需要\(O(L)\)的时间,L表示最短路径的长度。
优先级的确定以及LC-检索
我们知道,节点优先级的选择和计算直接影响搜索空间树的复杂程度,进而直接影响算法性能,我们希望具有如下特征的活节点称为当前扩展节点:
- 以X为根的子树中含有问题答案的答案节点;
- 在所有满足1的节点中,X距离答案节点最近。
我们希望我们定义的优先级可以尽快找到具有上述特征的节点,我们自然希望付出尽可能小的优先级计算成本。那么对于任意节点,搜索成本可以使用两种标准来衡量:
- 在生成一个答案节点之前,子树X需要生成的节点数,我们希望子树X快速生成答案节点;
- 以X为根的子树中,距离X最近的那个答案节点到X的路径长度。
那么我们用\(c()\)表示最小搜索成本函数,递归地定义如下:


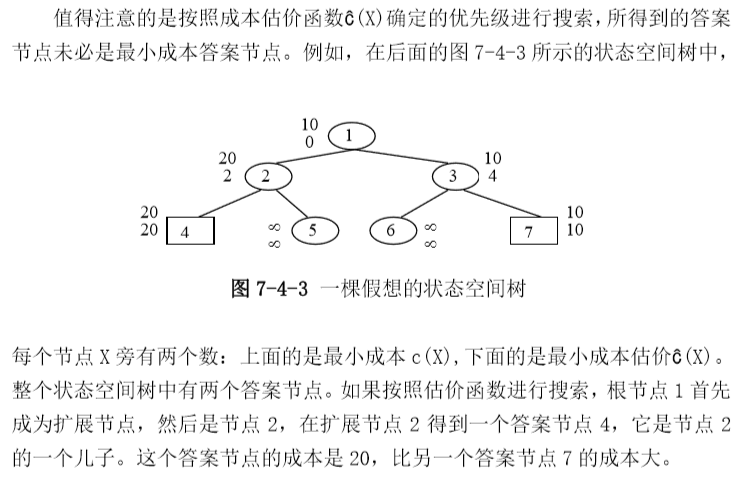



其实上述的伪代码只要掌握了0/1背包的分支限界法就很好理解了。需要注意的地方在上面的0/1背包问题都提到了。
旅行商问题