洛谷T236448 求二叉树中节点间的宽度

题目描述

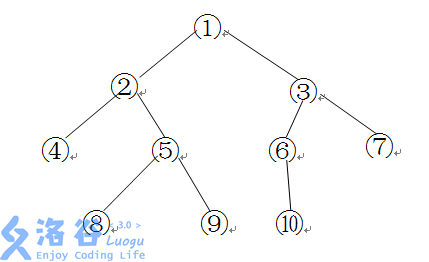
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 (3×2+2=8)

⑥→⑦为3 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。

输入格式

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

输出格式

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

输入输出样例

输入 #1复制

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

输出 #1复制4

4
8


解题思路：

可以先把这道题分解成3个小问题：

1：求二叉树的深度

2：求二叉树的宽度

3：求给定两个结点间距离

---

先来解决第一个问题：求深度

这个问题很好解决

每一个子结点的深度都是它父亲节点的深度+1（一号结点的深度是1）

这个部分很好理解；接下来上这一部分的代码：

for(int i = 1;i < n;i++){               //注意这里循环是到n - 1，按照题目要求，前n - 1行才是需要的
    cin >> root[i] >> son[i];           //我个人喜欢用cin和cout,而且这个题数据点不大，cin cout 没问题
    depth[son[i]] = depth[root[i]] + 1; //子结点的深度是父亲结点的深度 + 1
    fa[son[i]] = root[i];               //一个结点的父亲结点是它本身
}
    int max_depth = 1;                      //用于记录深度
    for(int i = 1;i <= n;i++){
    max_depth = max(max_depth,depth[i]);//求出深度
    width[depth[i]]++;                  //这里是为下一步做准备，再循环统计一次有点浪费
}

然后来解决第二个问题：求宽度

同样，这个问题很好解决

刚才求过了每一个深度都有几个结点（width[depth[i]]++;）

所以思路也很明确了

int max_width = 1;
for(int i = 1;i <= n;i++){
    max_width = max(max_width,width[i]);
}
    //这里应该没有什么好解释的

接着，就是本题的的重头戏：求给定两个结点间距离

思路一（本思路有误）：

我的第一反应是分别求出两个结点与1号结点的深度差（因为题目的举的第一个例子求得就是与一号节点的深度差，然后我就没看第二个例子了 QAQ ）

思路二（正确思路）：

求两个结点的最近公共祖先 LCA（一个结点是它所有子树上的点的祖先 这是给不懂的像一个月前的我的初学这说明的，大佬们请忽略）

求 LCA 的方法应是树上倍增

但是这题数据太小了，所以我就用暴力来求解：

int lca(int x,int y){
        if(x == y){
        return x;                  //两个点如果相同，那么 LCA 就是它本身
    }
    else if(depth[x] == depth[y]){  
        return lca(fa[x],fa[y]);   //如果两个点深度相同，就访问它们的父亲结点
    }
    else if(depth[x] < depth[y]){
         return lca(x,fa[y]);       //如果x的深度小于y的深度，就访问y的父亲结点，直到x y 深度相同
    }
    else{
         return lca(fa[x],y);       //原理大致和上一种情况相同，这里就不多解释了
    }
}

CODE：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int n;
int fa[101],root[101],son[101];

int depth[101],width[101];
int lca(int x,int y){
    if(x == y){
        return x;
    }
    else if(depth[x] == depth[y]){
        return lca(fa[x],fa[y]);
    }
    else if(depth[x] < depth[y]){
        return lca(x,fa[y]);
    }
    else{
        return lca(fa[x],y);
    }
}

int main(){
    cin >> n;
    depth[1] = 1;
    for(int i = 1;i < n;i++){
        cin >> root[i] >> son[i];
        depth[son[i]] = depth[root[i]] + 1;
        fa[son[i]] = root[i];
    }
    int x,y;
    cin >> x >> y;
    int max_depth = 1;
    for(int i = 1;i <= n;i++){
        max_depth = max(max_depth,depth[i]);
        width[depth[i]]++;
    }
    cout << max_depth << endl;
    int max_width = 1;
    for(int i = 1;i <= n;i++){
        max_width = max(max_width,width[i]);
    }
    cout << max_width << endl;
    int k = lca(x,y);      //求 LCA 的结点序号
    cout << (depth[x] - depth[k]) * 2 + depth[y] - depth[k];      //求距离
    return 0;
}