0918高数一千题，多元函数积分学

合集 - 考研倒计时100天の日常(9)

1.09132024-09-132.09142024-09-143.09152024-09-154.09162024-09-16

5.0918高数一千题，多元函数积分学2024-09-18

6.09202024-09-207.09212024-09-218.09222024-09-229.10022024-10-02

收起

 

T17.第一型曲线积分空间形式

用斯托克斯公式化成第二型曲面积分

解第二型曲面积分，用高斯公式或者投影转换法，后者注意正负号，上正下负，前正后负

T18.换路径，但是x=1左半段不能化成lnx算

T19.求偏导就对对应字母求就行，不用对y导x

T20.多元极值

• AC-B²＞0

1. A>0,极小
2. A<0，极大；

• AC-B²=0，不好说，现场判断
• AC-B²<0，非极值

T25.关于z的两个式子，求z对x的偏导时，选没有参数的，简化计算

T26.第一二型曲面积分的联系

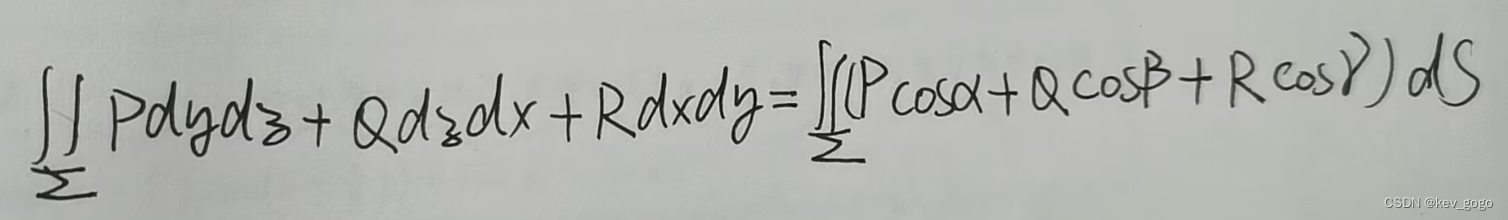
T28.目前做到的综合性最高的一个题

• 首先补面，高斯公式，减去补的那面，求面积
• 求面积时，将第二型曲面积分换成第一型，通过垂直于平面的单位法向量

　　　　其中法向量求法两种情况：参数式（对t,x,y,z都同理）；F（x,y,z）,对（x,y,z）各自求偏导

　　　　然后单位化

• 对高斯公式的那项求体积，利用微积分现场求，式子复杂不好求，但求得圆心到平面的距离为1，由对称性，可以求垂直的，反正相同。
• 结束

非常好题目，是我受益良多

T29.对于第二型曲面积分，含有f(x,y)这类抽象函数式时，建议用转换投影法（注意正负），以便于消去抽象式

T30.求x^2/3+y^2/3=1,x,y大于等于0围起来的面积,令x=(sint)³ ,然后用华理士公式

T31.换元时，雅各比行列式的计算