codeforces 848B Rooter's Song 思维题
http://codeforces.com/problemset/problem/848/B
给定一个二维坐标系,点从横轴或纵轴垂直于发射的坐标轴射入(0,0)-(w,h)的矩形空间。给出点发射的坐标轴,位置,延迟时间,发生碰撞则交换方向。求最后每个点的射出位置。
首先我们观察能得出两个结论,1. 类似蚂蚁爬树枝的问题,相遇只会交换方向,所以最后的射出点集只会因为碰撞而改变动点与射出点的对应关系,而不会增加减少射出点集。2.我们根据其射入位置和延迟时间可以计算出一个值v=pos-time,只有这个值相等才可能发生碰撞。
这样我们可以把所有点根据值v分成若干个集合,每个集合互不干涉,对于一个集合的射出点集,我们只要处理内部的对应关系即可。
首先画一张图片,代表一个集合的所有点,因为v相等,只要在图中的射线可以相遇一定会碰撞。
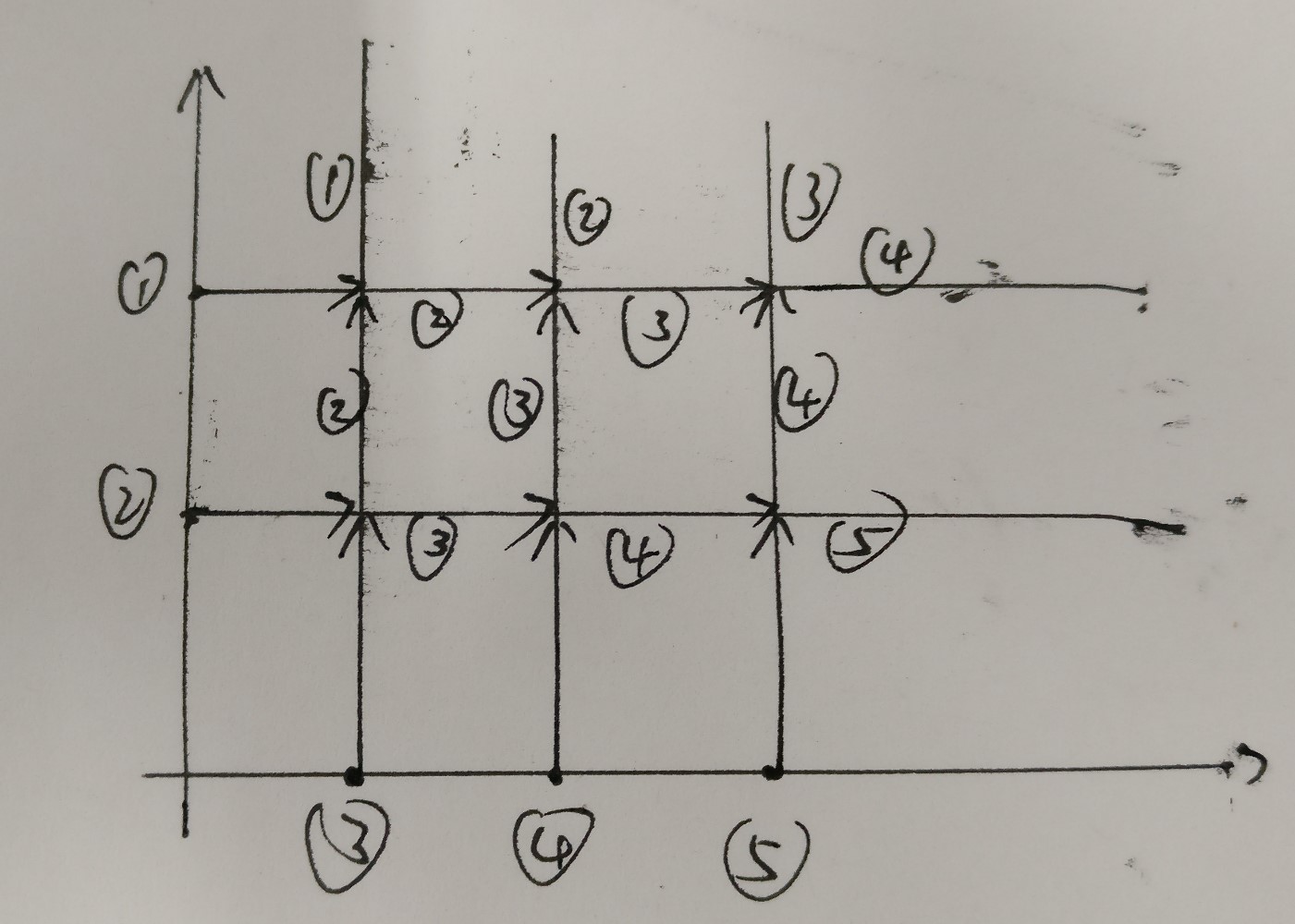
可见一个点从出发后,将依次交替遭遇另一个轴的点(数量为siz0)和本轴坐标大于等于本身的点(数量为siz1)。最终不再碰撞时的方向我们可以很容易地通过siz0,siz1推出来,而方向与最后一次碰撞的点相同(当与当前方向的平行的坐标轴发射的动点数量用尽时就不再碰撞了)。
这样每个点都可以在O(1)或O(log(n))下求出射出位置。因为需要排序预处理,所以要不要优化到O(1)并不是很重要。
#include <iostream> #include <string> #include <algorithm> #include <vector> #include <cmath> #include <cstring> #include <set> #include <map> #include <queue> #define LL long long using namespace std; const LL N = 100005; LL n, w, h; struct node { LL g, p, t; }; map<LL, vector<LL> > g[2]; node v[N]; int main() { cin.sync_with_stdio(false); while (cin >> n>>w>>h) { g[0].clear(), g[1].clear(); for (int i = 0; i < n; i++) { node temp; cin >> temp.g >> temp.p >> temp.t; temp.g--; g[temp.g][temp.p - temp.t].push_back(temp.p); v[i] = temp; } for (map<LL, vector<LL> >::iterator it = g[0].begin(); it != g[0].end(); it++) sort(it->second.begin(), it->second.end()); for (map<LL, vector<LL> >::iterator it = g[1].begin(); it != g[1].end(); it++) sort(it->second.begin(), it->second.end()); for (int i = 0; i < n; i++) { node e = v[i]; int dg; if (e.g == 0) { dg = 1; LL siz[2]; siz[e.g]= g[e.g][e.p - e.t].end() - lower_bound(g[e.g][e.p - e.t].begin(), g[e.g][e.p - e.t].end(), e.p); siz[dg] = g[dg][e.p - e.t].size(); LL miz = min(siz[0], siz[1]); if (siz[e.g] <= siz[dg]) cout << w << ' ' << g[dg][e.p - e.t][miz-1] << endl; else cout << g[e.g][e.p - e.t][g[e.g][e.p - e.t].size()-siz[e.g]+miz] << ' ' << h << endl; } else { dg = 0; LL siz[2]; siz[e.g] = g[e.g][e.p - e.t].end() - lower_bound(g[e.g][e.p - e.t].begin(), g[e.g][e.p - e.t].end(), e.p); siz[dg] = g[dg][e.p - e.t].size(); LL miz = min(siz[0], siz[1]); if (siz[e.g] <= siz[dg]) cout << g[dg][e.p - e.t][miz-1]<<' '<<h << endl; else cout << w<<' '<<g[e.g][e.p - e.t][g[e.g][e.p - e.t].size() - siz[e.g] + miz]<<endl; } } } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号