【例题收藏】◇例题·6◇ 电压机制(voltage)
◆例题·6◆ 电压机制
周六日常模拟赛……已经不知道该说什么了(感觉做不出来的都是好题)
▷ 题目
(终于不用自己翻译英文题了╮(╯-╰)╭)
【问题描述】
科学家在“无限神机”(Infinity Machine)找到一个奇怪的机制,这个机制有N个元件,有M条电线连接这些元件,所有元件都是连通的。两个元件之间可能有多条电线连接。
科学家对这些元件可以任意地设置为“高电压”和“低电压”两种模式,如果一条电线的一端为高电压,另一端为低电压,这条电线就会产生电流。
为了安全的研究“无限神机”,科学家需要找到一条电线,将它的两端设为相同的电压,并且除选择的这条电线外,其它所有电线都有电流(否则就没有研究的价值了)。
有多少条电线满足这样的条件?
【输入格式】
从文件 voltage.in 中读入数据。
输入的第一行包含两个正整数 n, m ,表示元件数和电线数。
接下来 m 行,每行两个整数 u, v,表示元件 u 和元件 v 有一条电线连接
【输出格式】
输出到文件 voltage.out 中。
输出一个整数,表示有多少条电线满足条件。
(鬼畜的题目背景就不copy上来了U•ェ•*U)
▷ 解析
首先很容易想到,节点的高/低电压就相当于0/1染色,除了题目所提到的“被选择的电线”,其他的边的两个端点的颜色应该不同。听起来是不是特别像二分图?所以可以套用一下判断二分图的DFS……检查是否染色成功。
接下来考虑一下图上的一些性质——环!
① 如果没有环
那么就非常简单了,由于图是全联通的,所以此时图就是一棵树。那么每一条边都可以作为“被选中的边”。原因是:
选择一条边就相当于把它删去,同时将它的两端点染成相同的颜色。但是由于图是一棵树,删除任意一条边都会将树分成两个连通块,两个连通块分别形成一个新的树。既然是树,从一个点开始,就一定可以将整棵树都染上色。
那么上述情况,答案就是边的数量。
② 如果有偶环
很容易想到不能选择在偶环上的边,否则染色就会失败。
比如下面这个例子:
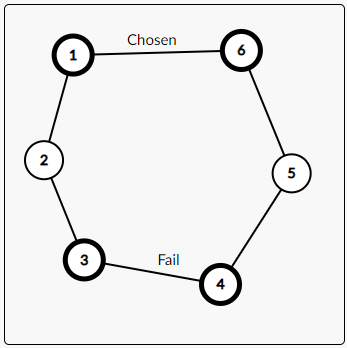
③ 如果有奇环
可以想到选择的边一定要在奇环中,否则会出现下面这种情况:{1,2,3,4,5}构成一个奇环,但是选择了1->6的边,也就相当于从1开始对奇环染色……很明显是无法完成的。
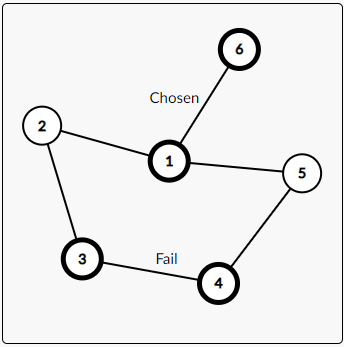
推广一下,对于每一个奇环,只要它没有一条边被选中,它就一定会从它的某一个点开始染色,而这样染色的结果就只有失败。所以所有奇环都必须包含有被选择的边,换句话说,如果我们计算出所有奇环的边集——我们能选择的边就只能是所有奇环的边集的交集!
综上所述,除了情况①,我们要选择的边E要满足以下性质:
1. 设第i个偶环的边集为 A[i] ,则对于每一个i, E ∉ A[i]
2. 设第i个奇环的边集为 B[i] ,则对于每一个i, E ∈B[i]
接下来就是进行一个DFS。由于下面要用到 DFS 树的一些知识,初学者可以先学一下 DFS树(不然可能会自闭(。・∀・)ノ)。
说明一下变量:
1. 整个图的奇环的个数为 odd。
2. 对于一条边存储一个 tot 值表示该边在多少个奇环内,则判断该边是否满足“包含在任何一个奇环内”时,只需要判断它的 tot 是否等于 odd 就可以了。
3. cnt[u] 表示 u 到 u的父亲(在DFS树里) 这一条边包含在多少个奇环里(差分数组)。
从1节点开始DFS,同时进行二分图染色。假设当时在节点u,准备扩展到与u相连的节点v —— 如果v没有染色,就将v染色,继续从v扩展;如果v已经染过色,那么 u->v 是一条返祖边,众所周知,u->v 的返祖边与 u->v 在DFS树上的路径会围成一个环。对于围成环的情况,判断当 u的颜色 和 v的颜色 相同时,就围成了一个奇环,否则围成了一个偶环。如果围成了一个奇环,则将环内的所有边的 tot 都+1;如果围成偶环,则将环内的所有边的 tot 都-1,这样的话 tot 就不可能达到 odd,也就不可能被选择了。
即使上述算法已经比较优秀了,但是仍然会爆炸,因为枚举环上的边时间复杂度太大了!
所以我们需要用到差分,差分数组最显著的性质就是 前缀和 等于原数组。当找到环时,如果是奇环,则 cnt[u]++,cnt[v]--,同时将 u->v 这条返祖边的 tot +1;如果是偶环,则 cnt[u]--,cnt[v]++,同时将 u->v 这条返祖边的 tot -1。除了在找到环时更改 cnt,在回溯时,父亲和儿子之间也存在 cnt 的转换——假设 点u,v 在DFS树中 u 是 v 的父亲,则 cnt[u]+=cnt[v] ,且 u->v 这一条树边的 tot 也 +=cnt[v]。
当整个 DFS 结束后,枚举所有边,判断它的 tot 是否等于 odd,如果是,则 ans++。
(我猜可能有一些 reader 已经自闭了,还是看看代码吧)
▷ 源代码
/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=100000,M=200000;
struct EDGE{
int u,v;
}edg[M+5];
struct LINK{
int v,id;
};
vector< LINK > lnk[N+5];
int n,m;
bool vis[M+5];
int col[N+5],cnt[N+5],tot[M+5],odd;
void DFS(int u){
for(int i=0;i<lnk[u].size();i++) //枚举相邻的点
if(!vis[lnk[u][i].id]){ //这条边没有被访问过(防止走重)
vis[lnk[u][i].id]=true;
int v=lnk[u][i].v;
if(col[v]!=-1){ //经过返祖边
if(col[v]==col[u]){
odd++; //奇环数量+1
cnt[u]++;cnt[v]--; //差分数组 u->v 的路径+1
tot[lnk[u][i].id]++; //返祖边+1
}
else{
cnt[v]++;cnt[u]--; //u->v路径-1,相当于取消选择 u->v 路径上任何一条边的可能性
tot[lnk[u][i].id]--; //取消选择返祖边的可能性
}
}
else{
col[v]=!col[u]; //染反色
DFS(v);
tot[lnk[u][i].id]+=cnt[v]; //父亲儿子之间的边统计
cnt[u]+=cnt[v]; //差分前缀和
}
}
}
int main(){
freopen("voltage.in","r",stdin);
freopen("voltage.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&edg[i].u,&edg[i].v);
lnk[edg[i].u].push_back((LINK){edg[i].v,i}); //双向连边
lnk[edg[i].v].push_back((LINK){edg[i].u,i});
}
memset(col,-1,sizeof col); //初始化所有颜色为-1
col[1]=0; //从节点1开始,先将它染成0
DFS(1);
int ans=0;
for(int i=1;i<=m;i++)
ans+=int(tot[i]==odd);
printf("%d\n",ans);
return 0;
}
The End
Thanks for reading!
- Lucky_Glass


