【前行】◇第3站◇ 国庆训练营·OI制模拟赛
【第3站】 国庆训练营·OI制模拟赛Ⅰ
怀着冲刺提高组400的愿望来到这个very small but very interesting 的训练营QwQ
在北大dalao的带领下开始了第一场OI模拟赛【炸心态ヽ(*。>Д<)o゜】
▶ 简单总结
感觉非常爆炸……
第一题还好,一眼看出结论题,所以开始打表……没想到只打出来了一种情况(为什么全是特殊情况),然后就凉了。
第二题就开始崩溃了。首先画图思考了大概20分钟……然后发现想不出正解,就开始想要骗分。看了看数据阶梯,发现自己好像只能做前1/3的数据,还要码一啪啦代码,顿时整个人都不好了。(脑子一团浆糊)打了一个LCA的版,就为了骗一点分。
第三题……连暴力都不知道怎么写,最后勉强一个搜索结束了整场比赛。
提高组的路还很长,还得慢慢走才行……ˋ( ° ▽、° )
(什么鬼“陈太阳”……由于是内部比赛,不能提供提交平台QwQ)
▶ 试题&解析
〔A〕陈太阳与取模
▷题目
给出一个区间[l,r]以及一个整数a,求有多少个整数x,使得对于每一个整数c∈[l,r]满足 c%a≡c (mod x)。如果存在无穷多给=个满足条件的x,输出-1,否则输出x的个数。
[规模] 多组数据(不超过100组),所有数均不超过1012。
▷解析
看到题目描述大概就是数学推导了。首先对于取模运算,我们并不陌生,但是我们还可以把它写成带余除法的形式——令 c mod a = b ,c = ka + b (b<a) 。那么我们就可以得到:b ≡ ka + b,也就是说 b mod x = ( ka + b ) mod x。
简单的拆开括号:b mod x = ka mod x + b mod x
移一下项:ka mod x = 0
那么k是什么? k = [ c / a ] ([]是向下取整)
所以 [ c / a ] * a 是 x 的倍数。
对于 [l,r] 中的每一个 c 都满足上述规律,所以 x 最大为 gcd( [ l / a ] * a , [ ( l + 1 ) / a ] * a , ... , [ r / a ] * a ) = gcd( [ l / a ] , [ ( l + 1 ) / a ] , ... , [ r / a ] ) * a。很容易想到:x的最大值的每一个因数也满足上述规律,那么问题就变成求 x 的最大值的因子个数。
首先因为 { [ l / a ] , [ ( l + 1 ) / a ] , ... , [ r / a ] } 是一个连续的非降序列,而相邻的两个正整数都是互质的,所以如果 [ l / a ] ≠ [ r / a ] ,则它们的gcd就等于1,否则它们就全都相等(也就是 [ l / a] ),则gcd为 [ l / a ] 。这样我们就可以求得x的最大值,从而以根号x的复杂度分解因数,就可以得到答案。
总体时间复杂度为 O( t * sqrt(a) )。
▷源代码
/*Lucky_Glass*/
//陈太阳与取模
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int main(){
int T;scanf("%d",&T);
while(T--){
ll l,r,a;
scanf("%lld%lld%lld",&l,&r,&a);
if(r<a){
printf("-1");
continue;
}
ll num,tot=0;
if(l/a==r/a) num=l/a;
else num=a;
for(ll i=1;i*i<=num;i++){
if(num%i==0){
ll A=i,B=num/i;
if(A==B) tot++;
else tot+=2;
}
}
printf("%lld",tot);
}
return 0;
}
〔B〕陈太阳与路径
▷题目
给出一个n个节点的树,对于每一个节点,求出它是多少条路径的中点(路径没有方向性,即 u->v 等同于 v->u )。
[规模] n≤500000
[注意] 路径的起点和终点可以是同一个点
▷解析
由于要统计个数,而且n比较大,还容易想到树形DP。
我们先固定1作为树根,那么对于一个节点u,如果以u为终点,那么路径的两端点有3种情况:
①在 u 的两个不同的子节点的子树中;
②一个在u的一个子节点的子树中,另一个是u的一个祖先;
③一个在u的一个子节点的子树中,另一个在u的一个祖先的子节点v(u不在v的子树中)的子树中。
举个例子:
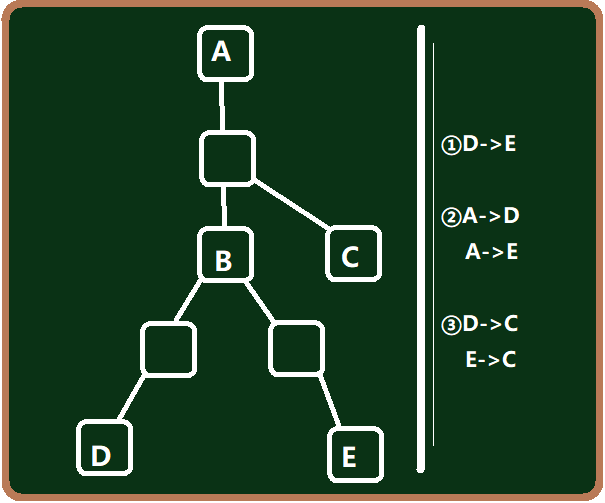
那么我们可以记从点u向下走i步能够走到的点的个数为 g[u][i] ,记从点u先向上走一步,再走(随意走,只要不回到u)(i-1) 步能走到的点的个数为 f[u][i]。
先求g[u][i]:
设v是u的一个儿子,那么g[u][i]则等于所有g[v][i-1]的和(先走到儿子v,再从v向下走i-1步)。
那么从根节点出发,一遍DFS就可以了。
再求f[u][i],需要用到 g:
设fa是u的父亲,那么f[u][i]可以理解为先走到父亲,再从父亲向上走一层到祖先,然后从祖先走(i-2)步,也就是f[fa][i-1];或者从父亲向下走(i-1)步,也就是g[fa][i-1],但是我们不能回到u,就必须减去从fa又走到u的情况,这时候可以看成从 u 出发向下走(i-2)步,也就是g[u][i-2]。所以最后可以得到:
f[u][i] = f[fa][i-1] + g[fa][i-1] - g[u][i-2];
当然我们会碰到i-2<0的情况,这时候就只减去回到u的情况,也就是减去1:
f[u][i] = f[fa][i-1] + g[fa][i-1] - 1;
这也可以一遍DFS做完。
最后统计答案其实可以在两遍DFS中一并求出,具体就看代码了……
▷源代码
/*Lucky_Glass*/
//陈太阳与路径
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const int N=500000;
int n;
vector<int> lnk[N+5];
int max_dep[N+5],fa[N+5];
vector<int> g[N+5],f[N+5];//down up
ll ans[N+5];
void DFS1(int u,int pre){
fa[u]=pre;
for(int i=0;i<lnk[u].size();i++){
int v=lnk[u][i];
if(v==pre) continue;
DFS1(v,u);
max_dep[u]=max(max_dep[u],max_dep[v]);
}
max_dep[u]++;
g[u].resize(max_dep[u]);f[u].resize(max_dep[u]);
g[u][0]=1;
for(int i=0;i<lnk[u].size();i++){
int v=lnk[u][i];
if(v==pre) continue;
for(int j=1;j<=max_dep[v];j++){
ans[u]+=1ll*g[v][j-1]*g[u][j];
g[u][j]+=g[v][j-1];
}
}
}
void DFS2(int u){
f[u][0]=1;
if(u==1) ans[u]++;//1'self
else{
for(int i=1;i<max_dep[u];i++){
f[u][i]=f[fa[u]][i-1]+g[fa[u]][i-1];
if(i>=2) f[u][i]-=g[u][i-2];
else f[u][i]--;
}
for(int i=0;i<max_dep[u];i++)
ans[u]+=f[u][i]*g[u][i];
}
for(int i=0;i<lnk[u].size();i++)
if(lnk[u][i]!=fa[u])
DFS2(lnk[u][i]);
}
int main(){
scanf("%d",&n);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
lnk[u].push_back(v);
lnk[v].push_back(u);
}
DFS1(1,0);
DFS2(1);
printf("%lld",ans[1]);
for(int i=2;i<=n;i++)
printf(" %lld",ans[i]);
return 0;
}
The End
Thanks for reading!
- Lucky_Glass


