【学时总结】◆学时·IX◆ 整体二分
◆学时·IX◆ 整体二分
至于我怎么了解到这个算法的……只是因为发现一道题,明显的二分查找,但是时间会爆炸,被逼无奈搜题解……然后就发现了一些东西QwQ
◇ 算法概述
整体二分大概是把BFS与二分查找完美结合了。
它针对一种可以用二分查找(直接查找答案),但是询问很多,对于每一个询问都做二分查找会超时的问题。
由于多次询问,那么问题的答案很可能在二分的区间中比较分散,那么我们可以用BFS枚举出二分将会产生的所有区间的情况……类似于线段树:
最初区间为 [1,m] 然后从该区间再拓展出 [1,mid][mid+1,m] …… 最后拓展到左端点等于右端点就可以得到答案。
那么我们知道——对于一个问题,它的解一定是区间的一个点——而一个区间,可能包含这个点。整体二分的思想,就是利用BFS可以存储数据的特点,用结构体NODE作为queue的类型。而每一个NODE节点描述了一个区间 [l,r] ,以及在这个区间里包含哪些问题的答案(用vector来存储)。BFS可以拓展到其他的节点,而这里我们的二分查找就类似于线段树,将原来的区间A一分为二为Lef,Rig,同时将A所包含的问题按它的答案的位置分配到Lef,Rig中,就完成了扩展。至于怎么分配问题……就看题目了。
当然也有可能在二分查找拓展出的一个区间中不包含任何一个问题的答案,这时候我们可以剪枝,因为这个区间无论怎么细分都无法得到任何一个问题的答案。
有一些题是不能用整体二分的,具体而言,能用整体二分的题目满足以下条件:
- 满足二分查找的单调性;
- 如果在区间[l,r]中包含某问题的解,则在[l,mid]或[mid+1,r]中也一定包含它的解;
- 问题的答案不一定是单独一个点,可以是多个点,分配问题时需要判断;
{下面就来看看到底哪些题目可以用整体二分吧(我目前只找到了一个,以后会继续更新( ̄▽ ̄)")}
◇ 例题简析
【Atcoder 1998】Stamp Rally
【题意】
给出一个无向图(n点m边),按照边输入的顺序编号为1~m。给出q个询问,每个询问[a,b,c]。对于每个询问定义一个花费 cst 为从a,b出发,到达恰好c个点所经过的最大边,求出对于每个询问的最小cst。
【样例&解析】

无向图:
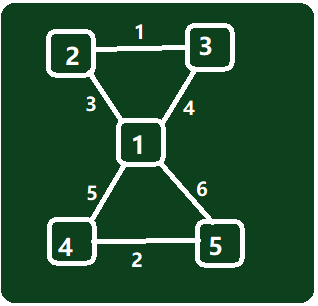
分别从2,3出发,到达3个点,则经过2->3,经过最大边(cst)最小为1;1,3出发到达4个点,则经过3->2,1->4,最大边最小为5……
【解析】
如果这道题只有一次询问的话,很容易想到二分查找。查找答案,即最大边编号,这样就相当于限制了能够经过哪些边。这是满足单调性的,也就是说当限制的最大边越大,就意味着能够通过的边就越多,则从给定点a,b出发能够到达的点一定会更多(或者不变)。那么我们就可以在[1,m]中二分答案,再每次Check从a,b能够到达的点的数量num,如果num>=c则缩小为左区间,否则缩小为右区间。
但是分析一下时间复杂度——二分查找O(logn),Check最坏情况O(n),总共q次询问……那么最后时间复杂度就是O(qnlogn),显然是爆炸的(>﹏<)。
虽然整体二分有一个非常奇怪的巨大的常数(STL的容器vector之类的总是有些奇怪的常数),但是总体来说运行速度还是快得多。
如何整体二分?我们需要定义一个结构体来存储一个二分状态——当前区间的左右端点l,r,以及答案在区间[l,r]内的询问(这里二分的就是询问的答案)。存储询问我又用了一个结构体,存储了询问的a,b点和c值,以及询问的编号,因为要离线处理(虽然说这个结构体没什么必要,但是好表示一些)。
struct PROBLEM {
int a,b,siz,id;
PROBLEM() {}
PROBLEM(int _a,int _b,int _siz,int _id):a(_a),b(_b),siz(_siz),id(_id) {}
};
struct NODE {
int l,r;
vector<PROBLEM> pro;
} beg;
由于题目保证所有询问都有解,所以所有问题的解应该都在[1,m]内,所以初始节点beg就是[1,m],然后包含的询问就是所有询问。
从这个节点开始拓展。扩展节点的方法是:
- 找到mid=(l+1)/2。
- 判断当限制mid为可以经过的最大边时,从a,b出发能够到达多少个点,记为num。
- 枚举包含在当前区间内的询问pro[i],若 num<pro[i].c 则分配给 [mid+1,r](mid小于询问答案);否则分配给 [l,mid](mid大于等于询问答案)。
- 当 l=r 时,则已经锁定到一个点,可以得出答案;当前包含在区间内的问题的答案为 l(r是一样的)。
- (可有可无,反正我没写 (●'◡'●))如果当前区间内不包含任何一个问题的解,剪掉。
基本框架就是这样,但是比较困难的就是求从a,b点出发,经过小于等于mid的边能够到达的点的个数了。由于这就是求a,b所在连通块的大小(删除大于mid的边),我借鉴了一种维护并查集的方法……首先对并查集进行一些改动——把并查集看成一棵树,然后维护一个以i为根的子树的大小sz[i]。这就意味着我们不能随意地将两个并查集合并,要遵循一定的顺序:
- 重置/初始化 并查集 Clear() —— 每个点都单独形成一个集合,同时也单独形成一棵树(只有一个节点),所以fa[i]=i,sz[i]=1;
- 查找祖先,即树根,Find() 没什么变化;
- 合并两个并查集,假设我们要合并u所在并查集和v所在并查集,则找到u,v分别所在树的根 preu,prev,如果preu=prev说明它们本来就属于一个集合,不需要合并,否则保留prev为树根,将preu连到prev上,作为一个儿子,以prev为根节点的树大小增加sz[u];
Okey!这样我们就可以统计a,b所在连通块即a,b所在树的大小了——当a,b属于同一棵树时,大小就是sz[Find(a)],否则就是 sz[Find(a)]+sz[Find(b)] 。但是对于每一个mid,并查集是不一样的……我们就需要每次清空并查集再重新建立,除非你用可持久化支持删边(当然我不愿意)。时间复杂度依旧很悬(>︿<)。那么就可以想一想,能否利用上一次计算出的并查集再加边形成现在需要的状态?我们可以记录一个las表示上一次并查集加入的边是 1~las 。如果las<mid,那么我们就可以把 las+1~mid 的边加入并查集,而不是重构并查集;但是如果las>mid,就只能重构了。
具体有一些细节上的优化,比如push状态时先左儿子,再右儿子,进行的重构操作会少一些……
(有什么问题我没有讲清楚?可以在文末的邮箱处问我(/▽\))
【源代码】
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int N=int(1e5);
int n,m,q;
int fa[N+5],sz[N+5],ans[N+5];
void Clear() {
for(int i=1; i<=n; i++)
fa[i]=i,sz[i]=1;
}
int Find(int u) {
if(fa[u]==u) return u;
else return fa[u]=Find(fa[u]);
}
void Link(int u,int v) {
int pre_u=Find(u),pre_v=Find(v);
if(pre_u==pre_v) return;
fa[pre_u]=pre_v;
sz[pre_v]+=sz[pre_u];
}
pair<int,int> edg[N+5];
struct PROBLEM {
int a,b,siz,id;
PROBLEM() {}
PROBLEM(int _a,int _b,int _siz,int _id):a(_a),b(_b),siz(_siz),id(_id) {}
};
struct NODE {
int l,r;
vector<PROBLEM> pro;
} beg;
int main() {
scanf("%d%d",&n,&m);
for(int i=1; i<=m; i++) {
int u,v;
scanf("%d%d",&u,&v);
edg[i]=make_pair(u,v);
}
scanf("%d",&q);
for(int i=0; i<q; i++) {
int a,b,siz;
scanf("%d%d%d",&a,&b,&siz);
beg.pro.push_back(PROBLEM(a,b,siz,i));
}
beg.l=1;
beg.r=m;
queue<NODE> que;
que.push(beg);
int las=0;
Clear();
while(!que.empty()) {
NODE pre=que.front(),R,L;
que.pop();
if(pre.l==pre.r) {
for(int i=0; i<pre.pro.size(); i++)
ans[pre.pro[i].id]=pre.l;
continue;
}
int mid=(pre.l+pre.r)>>1;
if(las>mid) {
las=0;
Clear();
}
while(las<mid) {
las++;
Link(edg[las].first,edg[las].second);
}
for(int i=0; i<pre.pro.size(); i++) {
int a=pre.pro[i].a,b=pre.pro[i].b,siz=pre.pro[i].siz,id=pre.pro[i].id;
int prea=Find(a),preb=Find(b),tot;
if(prea==preb) tot=sz[prea];
else tot=sz[prea]+sz[preb];
if(tot<siz) R.pro.push_back(PROBLEM(a,b,siz,id));
else L.pro.push_back(PROBLEM(a,b,siz,id));
}
L.l=pre.l;
L.r=mid;
R.l=mid+1;
R.r=pre.r;
que.push(L);
que.push(R);
}
for(int i=0; i<q; i++)
printf("%d\n",ans[i]);
return 0;
}
The End
Thanks for reading!
- Lucky_Glass


