【前行】◇第3站◇ Codeforces Round #512 Div2
【第3站】Codeforces Round #512 Div2
第三题莫名卡半天……一堆细节没处理,改一个发现还有一个……然后就炸了,罚了一啪啦时间
Rating又掉了……但是没什么,比上一次好多了:)
◇ 简单总结
前两道题非常OK,秒掉还好。心态爆炸是从第三题开始的……一开始设计的判断方法没有考虑0,然后就错了很多次,然后改了过后又没有考虑整个数要分成2个及以上的数,继续WA,最后整个程序删了重新魔改了一次终于AC。感觉最后的AC代码的复杂度要比原来高一些,但是毕竟AC了,还是不错的(似乎并不是复杂度越低越好)。
然后基本上历程是这样的:
看前两题 -> 愉快砍掉 -> 看三题 -> 好像很简单:) -> 提交 -> WA了! -> 开始改 -> 迅速发现bug -> 改了 -> 再交 -> 继续WA:( -> 上述过程重复7次QwQ -> 开始看D题 -> 看懂了 -> 好像不好做 -> 突然灵感乍现 -> 回过头做C题 -> AC了 -> 比赛结束
◇ 题目&解析
A. In Search of an Easy Problem
· [翻译]
出题人正在尝试把第一题出得更简单。于是他调查了n个人,如果第i个人觉得题比较难,出题人就会得到反馈“1”,否则得到反馈“0”。当出题人得到所有反馈都是“0”时,这道题就被认为是简单的。
输入n,表示调查人数。给出n个数 0 或 1 表示每个人的反馈。
如果该问题被认为是简单的,则输出"EASY",否则输出"HARD"。
· [解析]
依次输入,用一个bool变量判断是否有出现“1”,如果有则输出"HARD",否则输出"EASY"。
· [源代码]
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int main() {
scanf("%d",&n);
bool x=false;
for(int i=0,num; i<n; i++) {
scanf("%d",&num);
x|=num;
}
printf("%s\n",!x?"EASY":"HARD");
return 0;
}
B. Vasya and Cornfield
· [翻译]
有一块边长为n的正方形的地中间有一个矩形的田,田的四角的坐标分别是(0,d),(d,0),(n,n−d)(n−d,n)。
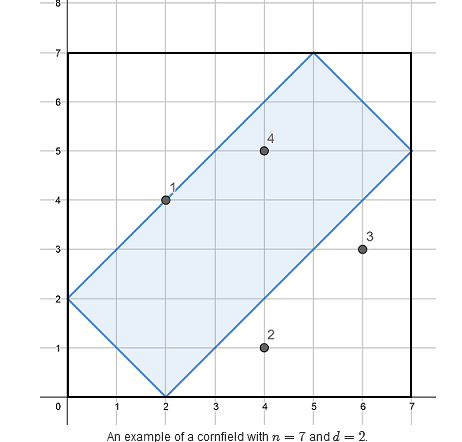
有m个蝗虫在这块地的某些坐标上,农夫想要知道哪些蝗虫在田里。
给出 n,d,m,以及每个蝗虫的坐标(均为整数,且矩形的每一条边都大于0),判断每个蝗虫是否在田里。
· [解析]
满满的全是“if”……
大概一开始我处理了一下图——如果d是大于n/2的,我就可以将原图左右翻转一下,把n-d作为新的d的值……也就是下面这样:
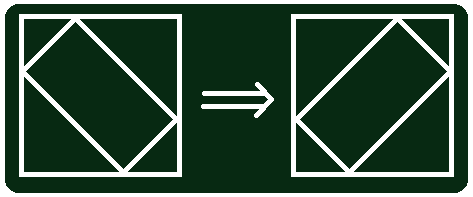
强行将情况转换一下……如果要进行这个操作,我就把bool变量flag赋值为true表示需要翻转。
之后输入虫的坐标时如果flag 为true,就把 x 改成 n-x,也就是进行一次翻转
接下来按虫的纵坐标分类讨论——
① 0≤y≤d : 在田里则是 d-y≤x≤d+y
② d<y<n-d : 在田里则是 y-d≤x≤y+d
③ n-d≤y≤n : 在田里则是 y-d≤x≤2n-d-y
输出即可。
· [源代码]
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,d,q;
int main() {
scanf("%d%d%d",&n,&d,&q);
bool flag=(n<d*2);
if(flag) d=n-d;
while(q--) {
int x,y;
scanf("%d%d",&x,&y);
if(flag) y=n-y;
if(y<=d) {
if(d-y<=x && x<=d+y)
printf("YES\n");
else
printf("NO\n");
} else if(d<y && y<n-d) {
if(y-d<=x && x<=y+d)
printf("YES\n");
else
printf("NO\n");
} else {
if(n-d-(n-y)<=x && x<=n-d+(n-y))
printf("YES\n");
else
printf("NO\n");
}
}
return 0;
}
C. Vasya and Golden Ticket
· [翻译]
Vasya有一个数字串,他希望把这个数字串分成多个(≥2)不重叠子串,且每个元素至少属于一个子串,满足每个子串中的数字之和相等。
输出是否可能。
· [解析]
首先可以用字符串储存数字串。
枚举第一个子串的范围为第 1~i 个数字。假设这样可行,则可以先算出每一个子串中的数字之gal和。用 tot 统计当前子串数字之和,依次枚举每一个数字,并加入到当前子串 —— 若tot>gal,则说明无法完成,如果tot==gal且下一位不是0(如果是0就可以继续添加到当前子串),则该子串已经达到目标,tot清零,记录下一个子串,用cnt记录分成的子串的个数。如果枚举到最后一个数字,则判断tot是否等于gal。特判一下——如果gal==0,就判断整个串是否都是0。
最后可以用bool保存答案,并判断cnt是否≥2,然后输出。
· [源代码]
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
char strnum[105];
int main() {
scanf("%d%s",&n,strnum);
int gal=0;
for(int i=0; i<n-1; i++) {
gal+=strnum[i]-'0';
int tot=0,cnt=0;
bool OK=true;
for(int j=0; j<n; j++) {
if(gal==0){
if(strnum[j]!='0'){
OK=false;
break;
}
else
cnt++;
}
else{
tot+=strnum[j]-'0';
if(tot>gal) {
OK=false;
break;
}
if(j==n-1 && tot!=gal) {
OK=false;
break;
}
if(tot==gal && strnum[j+1]!='0') tot=0,cnt++;
}
}
if(OK && cnt>=2) {
printf("YES\n");
return 0;
}
}
printf("NO\n");
return 0;
}
The End
Thanks for reading!
- Lucky_Glass


