【前行&赛时总结】◇第2站&赛时·8◇ Atcoder ABC-109
【第2站&赛时·8】 ABC-109
把最后一题题意理解错了……在第二组数据卡了好久(然而并不知道是special judge)QwQ
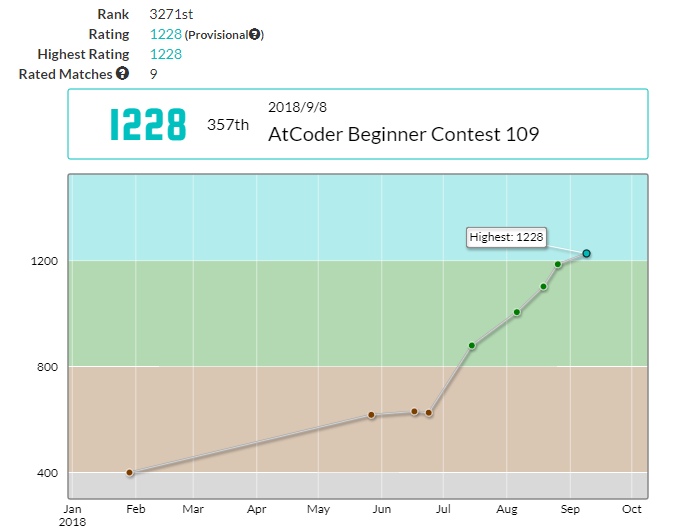
最终AK,速度慢了一些 Rank:357 Rating:1228(+41)
◇ 简单总结
第一二题如往常一样水过去了,然后发现第三题也不怎么难,题目看懂过后就只是一个数学的GCD,只是代码写完过后不知道为什么断网了,差不多六七分钟才提交代码TAT……
第四题就是一道奇妙的贪心构造题(我觉得应该是这样),只是一开始没读懂题目,一直在纠结为什么第二组样例为什么要进行最后一次操作,最后发现其实不需要满足操作次数最少😂,然后就AK了。
不得不说,蓝名是靠着ABC一点一点蹭上去的,不过上了蓝色,就意味着我不再是一个“Beginner”了,接下来便是 ARC 和 AGC 的历练了😄

哈~可真是不容易🙃
◇ 题目&解析
◆A题◆ ABC333 ❄数学❄ +传送门+
【题意】
给出在1~3的整数A,B,求是否有一个1~3的整数C满足A*B*C为奇数。存在输出“Yes”否则输出“No”。
【解析】
由于 偶*奇=偶 且 偶*偶=偶 ,所以A,B中只要出现一个偶数,则最后的结果都会是偶数,那么我们就是要判断 A,B 是否都是奇数,是则为Yes,只要有一个不是奇数,则是No。
【源代码】
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int main() {
int A,B;
scanf("%d%d",&A,&B);
if(A%2 && B%2) printf("Yes\n");
else printf("No\n");
return 0;
}
◆B题◆ Shiritori ❄模拟❄ +传送门+
【题意】
一个单词接龙游戏:①同一个单词不能出现多次;②除第一个单词,第i个单词开头字母必须是第i-1个单词末尾字母;
给出n个单词,判断“按照输入顺序说出单词,是否满足游戏要求”。
【解析】
n不大,没有必要用字符串hash,直接用map映射判重。用last存储上一个单词的末尾字符(初始值为第一个单词的末尾字符),从第一个单词后判断单词开头是否是last,并每次更新last为当前单词末尾。
【源代码】
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<iostream>
using namespace std;
int n;
string str;
map<string,bool> vis;
int main() {
scanf("%d",&n);
char last;
cin>>str;
last=str[str.length()-1];
vis[str]=true;
for(int i=1; i<n; i++) {
cin>>str;
if(vis[str] || str[0]!=last) {
printf("No\n");
return 0;
}
last=str[str.length()-1];
vis[str]=true;
}
printf("Yes\n");
return 0;
}
◆C题◆ Skip ❄数学计算❄ +传送门+
【题意】
有n座城市位于一条数轴上,没有两个城市的坐标相同。现在你站在坐标X(X不在任何一个城市),你每次可以向左或向右移动K个单位(即+K或-K)。求出一个最大的K,使得你能从X到达每一个城市。
给出n,X,以及每个城市的坐标 xi。求最大的K。
【解析】
如果要从X能够到达每一个城市,则X与各城市的距离都是K的倍数!由于K要最大,则K是X与各城市距离的最大公因数。
话是这么说,但是我比赛的时候有点糊涂,用的是另外一种方法🤨——把X也看成一个城市,一开始位于最左边的城市,一直向右跳,则应该每次都从第i个城市到第i+1个城市,所以K必须是所有相邻的城市的距离的最大公因数。实现就比一开始说的方法复杂……
【源代码】
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
typedef long long ll;
ll GCD(ll a,ll b) {
ll r;
while(b) {
r = b;
b = a % b;
a = r;
}
return a;
}
int n;
set<ll> num;
int main() {
scanf("%d",&n);
for(int i=0,pos;i<=n;i++)
scanf("%d",&pos),
num.insert(1ll*pos);
ll las=0,ans;
for(set<ll>::iterator it=num.begin();it!=num.end();it++){
ll val=*it;
if(!las) {las=val;continue;}
if(las==*num.begin()) ans=val-las;
else ans=GCD(ans,val-las);
las=val;
}
printf("%lld\n",ans);
return 0;
}
◆D题◆ Make Them Even ❄贪心+构造❄ +传送门+
【题意】
有一个r*c的矩阵,矩阵的每个点上都放了0~9个硬币。你可以进行0~r*c次操作:选取一个点(x,y),满足这个点在之前的操作中没有选中过,且该点上有硬币,然后将(x,y)的一个硬币移动到它周围的点上(四连通,上下左右)。所有操作完成后,使得矩阵中硬币个数为偶数的点的数量最大。注意:不要求操作次数最少。
输出操作次数m,再输出m行,每行包含整数 x,y,x',y',描述一次将(x,y)的一个硬币移动到(x',y')上的一次操作。
【解析】
首先是几个简单的贪心思想:
① 不移动为偶数的硬币;
② 不重复移动,即将(x,y)移动到(x',y')又将(x',y')移动到(x,y);
③ 如果矩阵所有的硬币总和是奇数,则最优解一定只有一个点是奇数,否则最优解的所有点都是偶数。
第③个结论是如何得来的呢?其实这就是得出答案的过程——
想象成一个推硬币游戏😶……从第一列开始推硬币,往右推,一直推到倒数第二列……设当前推到了第j列,若(i,j)是奇数,则把(i,j)的一个硬币推到(i,j+1)。因为最后一列的右边没有点,就不推了。这样推一次后,第一列到倒数第二列都会变成偶数(只要是奇数就推走一个,就变成了偶数)。那么我们可以想到,此时最后一列可能仍然存在奇数,那么我们从最后一列的第一行开始往下推,类似与之前推的规则,如果(i,c)为奇数,则向下(i+1,c)推,这样(i,j)就变成了偶数。因为点(r,c)已经没有地方推了,此时的奇偶性就确定了。容易理解,点(r,c)的奇偶性和矩阵中硬币总数的奇偶性是一致的。
上述“推”就是一次操作。为什么这就是最优解?考虑一次将(x,y)移动到(x',y')的操作——操作前(x,y)为奇数,那么操作后(x,y)为偶数,如果操作前(x',y')为奇数,则操作后为偶数,矩阵中偶数点个数+2,如果操作前为偶数,则操作后为奇数,矩阵中偶数点的个数不变。如果我们每次都对奇数点进行操作,可以想到,矩阵中要么只剩一个奇数点,要么没有奇数点,此时为最优解(因为无论如何都无法使偶数点变多了)。
【源代码】
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=500;
struct ANS {
int a,b,c,d;
ANS(int x,int y,int z,int w):a(x),b(y),c(z),d(w) {};
};
vector<ANS> ans;
int r,c;
int val[N+5][N+5];
bool vis[N+5][N+5];
int main() {
scanf("%d%d",&r,&c);
for(int i=0; i<r; i++)
for(int j=0; j<c; j++)
scanf("%d",&val[i][j]),
val[i][j]&=1; //只保存奇偶性
for(int i=0; i<r; i++) //推第一列到倒数第二列
for(int j=0; j<c-1; j++) //把(i,j)推到(i,j+1)
if(val[i][j]) //只操作奇数点
val[i][j+1]^=val[i][j],
ans.push_back(ANS(i+1,j+1,i+1,j+2)); //保存操作
for(int i=0; i<r-1; i++) //推最后一列
if(val[i][c-1]) //之推奇数
val[i+1][c-1]^=val[i][c-1],
ans.push_back(ANS(i+1,c,i+2,c)); //保存操作
//P.S. "^"是异或,这里用来改变奇偶性
printf("%d\n",ans.size());
for(int i=0; i<ans.size(); i++)
printf("%d %d %d %d\n",ans[i].a,ans[i].b,ans[i].c,ans[i].d);
return 0;
}
◇ 感悟
不再是一个Beginner了……该拿ARC练练手了😕。或许是一个新的起点,新的goal吧!
The End
Thanks for reading!
- Lucky_Glass


