【杂题总汇】HDU2018多校赛第九场 Rikka with Nash Equilibrium
【HDU2018多校赛第九场】Rikka with Nash Equilibrium
又是靠这样一道题擦边恰好和第两百名分数一样~愉快🙃
◇ 题目
<简要翻译>
构造一个r*c的矩阵,矩阵内的元素为 1~r*c ,且每个元素只出现一次(即矩阵的元素是1~r*c的一个排列)。
定义一种特殊数 x 当且仅当在矩阵中 x 同时是其所在行的最大值和所在列的最大值。例如:

现要求构造出的矩阵中恰好有一个特殊数,求能够构造出多少个不同矩阵,将所得答案模mod。
<输入&输出>
第一行一个整数T,表示数据的组数。每组数据包含一行——3个整数r,c,mod。每行输出一个整数,表示每组数据的答案。
<样例&解析>
| Input | Output | Explain |
|
2 3 3 100 5 5 2333 |
64 1170 |
对于第一组数据,一组解为: | 3 9 2 | | 6 4 5 | | 7 8 1 | 其中特殊数为9. |
◇ 解析
因为每个元素在矩阵中只出现一次,且最大元素是 r*c ,所以 r*c 的元素一定是一个特殊数(矩阵中没有比它大的数,所以行和列中也没有)。所以除了 r*c 以外没有其他的特殊数。
考虑该矩阵的构造方式,把元素1~r*c从大到小放入矩阵中。第一个元素可以放在任意一个位置,则有 r*c 种方案。设现在正在放第i个(非第一个)元素,为了防止当前元素成为特殊数,则应该放在之前放置的元素所在的行或列,因为如果不这样放置,之后放置的元素都将比第i个元素小,所以元素i所在行和列都不存在比它大的元素,也就成了特殊数,不满足条件。若按照该规则放置,则有三种情况:
① 第i个元素的所在列有之前放置的元素,但行没有;
② 第i个元素的所在行有之前放置的元素,但列没有;
③ 第i个元素的所在行和列都有之前放置的元素。
我们可以发现第一个元素放在任意位置,能够形成的方案数都是相同的。所以我们可以通过DP来解决这道题!
这道题影响答案的只有 “当前放置的元素”k,“已经放置有元素的行数”i,“已经放置有元素的列数”j。则dp[i][j][k]表示放置k后已经有i行、j列放置了元素。很容易发现,从小到大放元素和从大到小是等价的!所以这里我从1开始放置,元素1可以放置在矩阵的任意位置,共 r*c 种方案,即 dp[1][1][1] 初值为 1(元素1放置后有一行、一列已经放置有元素)。对于上述的三种情况写出转移式:
① 第i个元素放置在已经有元素的列上,但行上没有其他元素,则行数增加1,从 dp[i-1][j][k-1] 转移,由于有j列已经放置元素,且有 [r-(i-1)] 行没有放置元素,则共 j*(r-i+1) 个位置可以放;
② 第i个元素放置在已经有元素的行上,但列上没有元素,与情况①恰好相反,共有 i*(c-j+1) 个位置;
③ 第i个元素放置的行和列上都有元素,则行列都不增加,即 dp[i][j][k-1] ,总共有 i*j 个位置是行和列上都有元素,但已经放置了(k-1)个元素在这些位置(因为在某位置放置一个元素后,该位置必然行和列都有元素,即放置的那个元素),所以剩余可以放的位置为 (i*j-k+1),此时需要保证 (i*j-k+1)为正数。
总结一下,得到状态转移方程式为:
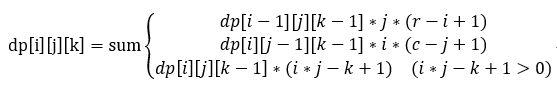
还是比较简洁,三重循环分别从大到小枚举 i,j,k 就可以了。注意开 long long ,处处取模!(最大为1e9,1e9*1e9时因为还没有模mod,会炸掉……)
最后输出答案就是dp[r][c][r*c],即每行都有元素,且已经放置了第r*c个元素。
◇ 源代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int r,c;
long long mod;
long long dp[85][85][6405];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d%lld",&r,&c,&mod);
memset(dp,0,sizeof dp);
dp[1][1][1]=1ll*r*c;
for(int i=1;i<=r;i++)
for(int j=(i==1?2:1);j<=c;j++)
for(int k=1;k<=i*j;k++)
{
int A=0,B=0,C=0;
A=dp[i-1][j][k-1]*j*(r-i+1)%mod;
B=dp[i][j-1][k-1]*i*(c-j+1)%mod;
if(i*j-k+1>=0)
C=dp[i][j][k-1]*(i*j-k+1)%mod;
dp[i][j][k]=((A+B)%mod+C)%mod;
}
printf("%lld\n",dp[r][c][r*c]%mod);
}
}
The End
Thanks for reading!
- Lucky_Glass


